1 Introduction
Observation of fluid flow in nature, laboratory experiments and numerical simulations has provided evidence of the existence of flow features and certain, but often complex, rules. For example, in nature, Kelvin–Helmholtz waves in clouds (Dalin et al. Reference Dalin, Pertsev, Frandsen, Hansen, Andersen, Dubietis and Balciunas2010), von Kármán vortices in ocean flow around an island (Berger & Wille Reference Berger and Wille1972) and the swirling great red spot on Jupiter (Marcus Reference Marcus1988) are flow structures that can be classified as a certain type of vortical motion produced by a distinct combination of boundary conditions and initial conditions for the governing first principles. Similar observations have also been reported in laboratory experiments and numerical simulations (Freymuth Reference Freymuth1966; Ruderich & Fernholz Reference Ruderich and Fernholz1986; Babucke, Kloker & Rist Reference Babucke, Kloker and Rist2008; Wu & Moin Reference Wu and Moin2009). The existence of distinct and dominant flow features has also been widely investigated by reduced-order models (ROMs) using mathematical decomposition techniques such as the proper orthogonal decomposition (POD) method (Sirovich Reference Sirovich1987), the dynamic mode decomposition (DMD) method (Schmid Reference Schmid2010) and the Koopman operator method (Mezić Reference Mezić2013; Morton et al. Reference Morton, Jameson, Kochenderfer and Witherden2018).
Owing to the existence of distinct or dominant flow features, animals such as insects, birds and fish are reported to be able to control their body movements in order to adapt their fluid dynamic environment and so improve their aero- or hydrodynamic performance and efficiency (Wu Reference Wu2011; Yonehara et al. Reference Yonehara, Goto, Yoda, Watanuki, Young, Weimerskirch, Bost and Sato2016). This suggests the possibility that they empirically learn to generate dominant fluid motions as well as the nonlinear correlation of fluid motions and are able to estimate future flow based on flow experienced in their environments. Such observations in nature motivate us to investigate the feasibility of predicting unsteady fluid motions by learning flow features using neural networks.
Attempts to apply neural networks to problems of fluid flow have been recently made by Tracey, Duraisamy & Alonso (Reference Tracey, Duraisamy and Alonso2015), Zhang & Duraisamy (Reference Zhang and Duraisamy2015) and Singh, Medida & Duraisamy (Reference Singh, Medida and Duraisamy2017), who utilized shallow neural networks for turbulence modelling for Reynolds-averaged Navier–Stokes (RANS) simulations. Ling, Kurzawski & Templeton (Reference Ling, Kurzawski and Templeton2016) employed deep neural networks to better model the Reynolds stress anisotropy tensor for RANS simulations. Guo, Li & Iorio (Reference Guo, Li and Iorio2016) employed a convolutional neural network (CNN) to predict steady flow fields around bluff objects and reported reasonable prediction of steady flow fields with significantly reduced computational cost than that required for numerical simulations. Similarly, Miyanawala & Jaiman (Reference Miyanawala and Jaiman2017, Reference Miyanawala and Jaiman2018) and Mao et al. (Reference Mao, Joshi, Miyanawala and Jaiman2018) employed CNNs to predict aerodynamic forces on bluff bodies, also with notably reduced computational costs. Those previous studies showed the high potential of deep learning techniques for enhancing simulation accuracy and reducing computational cost.
Predicting unsteady flow fields using deep learning involves extracting both spatial and temporal features of input flow field data, which could be considered to be learning videos. Video modelling enables prediction of a future frame of a video based on information from previous video frames by learning the spatial and temporal features of the video. Although deep learning techniques have been reported to generate high-quality real-world-like images in image modelling areas (Denton, Chintala & Fergus Reference Denton, Chintala and Fergus2015; Radford, Metz & Chintala Reference Radford, Metz and Chintala2015; van den Oord et al. Reference van den Oord, Kalchbrenner, Espeholt, Vinyals and Graves2016a ; van den Oord, Kalchbrenner & Kavukcuoglu Reference van den Oord, Kalchbrenner, Kavukcuoglu, Florina Balcan and Weinberger2016b ), it is known that, for video modelling, deep learning techniques have presented difficulties in generating high-quality prediction due to blurriness caused by complexity in the spatial and temporal features in a video (Ranzato et al. Reference Ranzato, Szlam, Bruna, Mathieu, Collobert and Chopra2014; Mathieu, Couprie & LeCun Reference Mathieu, Couprie and LeCun2015; Srivastava, Mansimov & Salakhudinov Reference Srivastava, Mansimov and Salakhudinov2015; Xingjian et al. Reference Xingjian, Chen, Wang, Yeung, Wong and Woo2015).
Mathieu et al. (Reference Mathieu, Couprie and LeCun2015) proposed a video modelling architecture that utilizes a generative adversarial network (GAN) (Goodfellow et al. Reference Goodfellow, Pouget-Abadie, Mirza, Xu, Warde-Farley, Ozair, Courville and Bengio2014), which combines a fully convolutional generator model and a discriminator model. The GAN was capable of generating future video frames from input frames at previous times. The generator model generates images and the discriminator model is employed to discriminate the generated images from real (ground truth) images. A GAN is adversarially trained so the generator network is trained to fool the discriminator network, and the discriminator network is trained not to be fooled by the generator network. The Nash equilibrium in the two-pronged adversarial training leads the network to extract underlying low-dimensional features in an unsupervised manner and, in consequence, good quality images can be generated. The most notable advantage of using the GAN is that, once it is trained, the network is able to generate predictions in a larger domain. This leads to a memory-efficient training of videos because the network can predict a frame with a larger size than that in training. A recurrent neural network (RNN) based architecture lends itself to learning the temporal correlation among encoded information in the past and thereby predicting future frames. It is also worth noting that, in the present study, the application of RNNs proposed by Srivastava et al. (Reference Srivastava, Mansimov and Salakhudinov2015) and by Xingjian et al. (Reference Xingjian, Chen, Wang, Yeung, Wong and Woo2015) has been attempted. However, it has been found that the methods are practical only for low-resolution frames since the number of weight parameters for the RNNs increases as a function of the square of the resolution of a frame. Ranzato et al. (Reference Ranzato, Szlam, Bruna, Mathieu, Collobert and Chopra2014) proposed a recurrent convolutional neural network (rCNN), which is also able to predict a frame with a larger size than that in training. However, Mathieu et al. (Reference Mathieu, Couprie and LeCun2015) reported that the GAN improves the capability for predicting future frames on a video dataset of human actions (Soomro, Zamir & Shah Reference Soomro, Zamir and Shah2012) compared to the rCNN, the predictions of which are more static for unsteady motions.
Prediction of unsteady flow fields using deep learning could offer new opportunities for real-time control and guidance of aero- or hydro-vehicles, fast weather forecasting, etc. As the first step towards prediction of unsteady flow fields using deep learning, the present study is an attempt to predict rather simple but canonical unsteady vortex shedding over a circular cylinder using four different deep learning networks: GANs with and without consideration of conservation laws and CNNs with and without consideration of conservation laws. Consideration of conservation laws is realized as a form of loss function. The aim of the present study is to predict unsteady flow fields at Reynolds numbers that were not utilized in the learning process. This differs from the aim of ROMs, which is to discover and understand low-dimensional representation of flow fields at certain Reynolds numbers by learning them (Liberge & Hamdouni Reference Liberge and Hamdouni2010; Bagheri Reference Bagheri2013).
The paper is organized as follows: the method for constructing flow field datasets and deep learning methods are explained in §§ 2 and 3, respectively. The results obtained using the present deep learning networks are discussed in § 4, followed by concluding remarks in § 5.
2 Construction of flow field datasets
2.1 Numerical simulations
Numerical simulations of flow over a circular cylinder at Reynolds number
$Re_{D}=U_{\infty }D/\unicode[STIX]{x1D708}=150$
,
$300$
,
$400$
,
$500$
,
$1000$
,
$3000$
and
$3900$
, where
$U_{\infty }$
,
$D$
and
$\unicode[STIX]{x1D708}$
are the free-stream velocity, cylinder diameter and kinematic viscosity, respectively, are conducted by solving the incompressible Navier–Stokes equations as follows:
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}u_{i}u_{j}}{\unicode[STIX]{x2202}x_{j}}=-\frac{1}{\unicode[STIX]{x1D70C}}\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x_{i}}+\unicode[STIX]{x1D708}\frac{\unicode[STIX]{x2202}^{2}u_{i}}{\unicode[STIX]{x2202}x_{j}\unicode[STIX]{x2202}x_{j}} & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{i}}=0, & & \displaystyle\end{eqnarray}$$
where
$u_{i}$
,
$p$
and
$\unicode[STIX]{x1D70C}$
are the velocity, pressure and density, respectively. Velocity components and the pressure are non-dimensionalized by
$U_{\infty }$
and
$\unicode[STIX]{x1D70C}U_{\infty }^{2}$
, respectively. A fully implicit fractional-step method is employed for time integration, where all terms in the Navier–Stokes equations are integrated using the Crank–Nicolson method. Second-order central-difference schemes are employed for spatial discretization and the kinetic energy is conserved by treating face variables as arithmetic means of neighbouring cells (You, Ham & Moin Reference You, Ham and Moin2008). The computational domain consists of a block structured H-grid with an O-grid around the cylinder (figure 1). The computational domain sizes are
$50D$
and
$60D$
in the streamwise and the cross-flow directions, respectively, where
$D$
is the cylinder diameter. In the spanwise direction,
$6D$
is used for flow at Reynolds numbers less than 1000, while
$\unicode[STIX]{x03C0}D$
is used otherwise. The computational time-step size
$\unicode[STIX]{x0394}tU_{\infty }/D$
of
$0.005$
is used for all simulations. The domain size, number of grid points and time-step sizes are determined from an extensive sensitivity study.
Figure 1. The computational domain for numerical simulations.
$N$
denotes the number of mesh points, where
$N_{x_{1}}=20$
,
$N_{x_{2}}=30$
,
$N_{x_{3}}=50$
,
$N_{x_{4}}=50$
$N_{y_{1}}=30$
,
$N_{y_{2}}=30$
,
$N_{y_{3}}=80$
and
$N_{\unicode[STIX]{x1D703}}=150$
. The domain size and the number of mesh points in the spanwise direction are
$6D$
(
$\unicode[STIX]{x03C0}D$
for flow at
$Re_{D}\geqslant 1000$
) and
$96$
, respectively.
2.2 Datasets
Flow fields in different vortex shedding regimes are calculated for training and testing deep learning networks. The following flow regimes and Reynolds numbers are considered: two-dimensional vortex shedding regime (
$Re_{D}=150$
), three-dimensional wake transition regime (
$Re_{D}=300,400$
and
$500$
) and shear-layer transition regime (
$Re_{D}=1000,3000$
and
$3900$
). Simulation results of flow over a cylinder at each Reynolds number are collected with a time-step interval of
$\unicode[STIX]{x1D6FF}t=20\unicode[STIX]{x0394}tU_{\infty }/D=0.1$
. Flow variables
$u_{1}/U_{\infty }(=u/U_{\infty })$
,
$u_{2}/U_{\infty }(=v/U_{\infty })$
,
$u_{3}/U_{\infty }(=w/U_{\infty })$
and
$p/\unicode[STIX]{x1D70C}U_{\infty }^{2}$
at each time step in a square domain of
$-1.5D<x<5.5D$
,
$-3.5D<y<3.5D$
,
$z=0D$
(
$7D\times 7D$
sized domain) are interpolated into a uniform grid with
$250\times 250$
cells for all Reynolds number cases. Thus, a dataset at each Reynolds number consists of flow fields with the size of
$250\times 250\;\text{(grid cells)}\times 4\;\text{(flow variables)}$
.
The calculated datasets of flow fields are divided into training and test datasets, so that flow fields at Reynolds numbers in the training dataset is not included in the test dataset. Flow fields in the training dataset are randomly subsampled in time and space into five consecutive flow fields on a
$0.896D\times 0.896D$
domain with
$32\times 32$
grid cells (see figure 2). The subsampled flow fields contain diverse types of flow, such as free-stream flow, wake flow, boundary layer flow or separating flow. Therefore, deep learning networks are allowed to learn diverse types of flow. The first four consecutive sets of flow fields are used as an input (
${\mathcal{I}}$
), while the following set of flow fields is a ground truth flow field (
${\mathcal{G}}({\mathcal{I}})$
). The pair of input and ground truth flow fields form a training sample. In the present study, a total of 500 000 training samples are employed for training deep learning networks. The predictive performance of networks is evaluated on a test dataset, which is composed of interpolated flow fields from numerical simulations on a
$7D\times 7D$
domain with
$250\times 250$
grid cells.
Figure 2. (a) Instantaneous fields of flow variables
$u/U_{\infty },v/U_{\infty },w/U_{\infty }$
and
$p/\unicode[STIX]{x1D70C}U_{\infty }^{2}$
on a
$7D\times 7D$
domain with
$250\times 250$
grid cells. (b) The procedure of subsampling five consecutive flow fields to the input (
${\mathcal{I}}$
) and the ground truth (
${\mathcal{G}}({\mathcal{I}})$
) on a
$0.896D\times 0.896D$
domain with
$32\times 32$
grid cells.
3 Deep learning methodology
3.1 Overall procedure of deep learning
A deep learning network learns a nonlinear mapping of an input tensor and an output tensor. The nonlinear mapping is composed of a sequence of tensor operations and nonlinear activations of weight parameters. The objective of deep learning is to learn appropriate weight parameters that form the most accurate nonlinear mapping of the input tensor and the output tensor that minimizes a loss function. A loss function evaluates the difference between the estimated output tensor and the ground truth output tensor (the desired output tensor). Therefore, deep learning is an optimization procedure for determining weight parameters that minimize a loss function. A deep learning network is trained with the following steps.
(1) A network estimates an output tensor from a given input through the current state of weight parameters, which is known as feed forward.
(2) A loss (scalar value) is evaluated by a loss function of the difference between the estimated output tensor and the ground truth output tensor.
(3) Gradients of the loss with respect to each weight parameter are calculated through the chain rule of partial derivatives starting from the output tensor, which is known as back propagation.
(4) The weight parameters are gradually updated in the negative direction of the gradients of the loss with respect to each weight parameter.
(5) Steps 1 to 4 are repeated until weight parameters (deep learning network) are sufficiently updated.
Figure 3. Illustration of a fully connected layer.
The present study utilizes two different layers that contain weight parameters: fully connected layers and convolution layers. An illustration of a fully connected layer is shown in figure 3. Weight parameters of a fully connected layer are stored in connections (
$W$
) between layers of input (
$X$
) and output (
$Y$
) neurons, where neurons are elementary units in a fully connected layer. Information inside input neurons is passed to output neurons through a matrix multiplication of the weight parameter matrix and the vector of input neurons as follows:
$$\begin{eqnarray}\displaystyle Y^{i}=\mathop{\sum }_{j}W^{j,i}X^{j}+\text{bias}, & & \displaystyle\end{eqnarray}$$
where a bias is a constant, which is also a parameter to be learned. An output neuron of a fully connected layer collects information from all input neurons with respective weight parameters. This provides strength to learn a complex mapping of input and output neurons. However, as the number of weight parameters is determined as the multiplication of the number of input and output neurons, where the number of neurons is generally in the order of hundreds or thousands, the number of weight parameters easily becomes more than sufficient. As a result, abundant use of fully connected layers leads to inefficient learning. For this reason, fully connected layers are typically used as a classifier, which collects information and classifies labels, after extracting features using convolution layers.
Figure 4. Illustration of a convolution layer.
An illustration of a convolution layer is shown in figure 4. Weight parameters (
$W$
) of a convolution layer are stored in kernels between input (
$X$
) and output (
$Y$
) feature maps, where feature maps are elementary units in a convolution layer. To maintain the shape of the input after convolution operations, zeros are padded around input feature maps. The convolution operation with padding is applied to input feature maps using kernels as follows:
$$\begin{eqnarray}\displaystyle Y_{i,j}^{n}=\left[\mathop{\sum }_{k}\mathop{\sum }_{c=0}^{F_{y}-1}\mathop{\sum }_{r=0}^{F_{x}-1}W_{r,c}^{n,k}\underbrace{X_{i+r,j+c}^{k}}_{\text{Pad}~\text{included}}\right]+\text{bias}, & & \displaystyle\end{eqnarray}$$
where
$F_{x}\times F_{y}$
is the size of kernels. Weight parameters inside kernels are updated to extract important spatial features inside input feature maps, so an output feature map contains an encoded feature from input feature maps. Updates of weight parameters could be affected by padding as output values near boundaries of an output feature map are calculated using parts of weight parameters of kernels, whereas values far from boundaries are calculated using all weight parameters of kernels. However, without padding, the output shape of a feature map of a convolution layer is reduced, which indicates loss of information. Therefore, padding enables a CNN to minimize the loss of information and to be deep by maintaining the shape of feature maps, but as a trade-off it could affect updates of weight parameters.
Convolution layers contain significantly fewer parameters to update, compared to fully connected layers, which enables efficient learning. Therefore, convolution layers are typically used for feature extraction.
After each fully connected layer or convolution layer, a nonlinear activation function is usually applied to the output neurons or feature maps to provide nonlinearity to a deep learning network. The hyperbolic tangent function (
$f(x)=\tanh (x)$
), the sigmoid function (
$f(x)=1/(1+\exp (-x))$
) and the rectified linear unit (ReLU) activation function (
$f(x)=\max (0,x)$
) (Krizhevsky, Sutskever & Hinton Reference Krizhevsky, Sutskever and Hinton2012) are examples of typically applied activation functions. In the present study, these three functions are employed as activation functions (see § 3.2 for details).
A max pooling layer is also utilized in the present study, which does not contain weight parameters but applies a max filter to non-overlapping subregions of a feature map (see figure 5). A max pooling layer can be connected to an output feature map of a convolution layer to extract important features.
Figure 5. Illustration of a
$2\times 2$
max pooling layer.
3.2 Configurations of deep learning networks
Deep learning networks employed in the present study consist of a generator model that accepts four consecutive sets of flow fields as an input. Each input set of flow fields is composed of flow variables of
$\{u/U_{\infty },v/U_{\infty },w/U_{\infty },p/\unicode[STIX]{x1D70C}U_{\infty }^{2}\}$
, to take advantage of learning correlated physical phenomena among flow variables. The number of consecutive input flow fields is determined by a parameter study. A high number of input flow fields increases memory usage and therefore the learning time. A low number might cause a shortage of input information for the networks. Three cases with
$m=2$
, 4 and 6 are trained and tested for unsteady flow fields. No significant benefit in the prediction is found with
$m$
beyond 4. The flow variables are scaled using a linear function to guarantee that all values are in
$-$
1 to 1. This scaling supports the usage of the ReLU activation function by providing nonlinearity to networks and the hyperbolic tangent activation function by bounding predicted values. Original values of the flow variables are retrieved by an inverse of the linear scaling. The generator model utilized in this study is composed of a set of multi-scale generative CNNs
$\{G_{0},G_{1},G_{2},G_{3}\}$
to learn multi-range spatial dependences of flow structures (see table 1 and figure 6). Details of the study for determining network parameters such as numbers of layers and feature maps are summarized in § C.1.
Table 1. Configuration of the generator model in GANs and multi-scale CNNs (see figure 6 for connections).
Figure 6. (a) Schematic diagram of generator models.
${\mathcal{I}}$
is the set of input flow fields (see figure 2) and
${\mathcal{I}}_{k}$
denotes interpolated input flow fields on an identical domain with
$1/(2^{k}\times 2^{k})$
coarser grid resolution.
$G_{k}$
indicates a generative CNN which is fed with input
${\mathcal{I}}_{k}$
, while
$G_{k}({\mathcal{I}})$
indicates the set of predicted flow fields from the generative CNN
$G_{k}$
.
$R_{k}\circ ()$
indicates the rescale operator, which upscales the grid size twice in both directions. (b) Example of input flow fields and the corresponding prediction of the flow field on a test data.
During training, a generative CNN
$G_{k}$
generates flow field predictions (
$G_{k}({\mathcal{I}})$
) on the
$0.896D\times 0.896D$
domain with resolution of
$32/2^{k}\times 32/2^{k}$
through padded convolution layers.
$G_{k}$
is fed with four consecutive sets of flow fields on the domain with
$32/2^{k}\times 32/2^{k}$
resolution (
${\mathcal{I}}_{k}$
), which are bilinearly interpolated from the original input sets of flow fields with
$32\times 32$
resolution (
${\mathcal{I}}$
), and a set of upscaled flow fields, which is obtained by
$R_{k+1}\circ G_{k+1}({\mathcal{I}})$
(see figure 6).
$R_{k+1}\circ ()$
is an upscale operator that bilinearly interpolates a flow field on a domain with resolution of
$32/2^{k+1}\times 32/2^{k+1}$
to a domain with resolution of
$32/2^{k}\times 32/2^{k}$
. Note that domain sizes for
$32/2^{k}\times 32/2^{k}$
and
$32\times 32$
resolution are identical to
$0.896D\times 0.896D$
, where the size of the corresponding convolution kernel ranges from 3 to 7 (see table 1). Consequently,
$G_{k}$
is able to learn larger spatial dependences of flow fields than
$G_{k-1}$
by sacrificing resolution. As a result, a multi-scale CNN-based generator model enables the learning and prediction of flow fields with multi-scale flow phenomena. The last layer of feature maps in each multi-scale CNN is activated with the hyperbolic tangent function to bound the output values, while other feature maps are activated with the ReLU function to provide nonlinearity to networks.
Let
${\mathcal{G}}_{k}({\mathcal{I}})$
be ground truth flow fields with resized resolution of
$32/2^{k}\times 32/2^{k}$
. The discriminator model consists of a set of discriminative networks
$\{D_{0},D_{1},D_{2},D_{3}\}$
with convolution layers and fully connected layers (see table 2 and figure 7). A discriminative network
$D_{k}$
is fed with inputs of predicted flow fields from the generative CNN (
$G_{k}({\mathcal{I}})$
) and ground truth flow fields (
${\mathcal{G}}_{k}({\mathcal{I}})$
). Convolution layers of a discriminative network extract low-dimensional features or representations of predicted flow fields and ground truth flow fields through convolution operations. Then
$2\times 2$
max pooling, which extracts the maximum values from each equally divided
$2\times 2$
sized grid on a feature map, is added after convolution layers to pool the most important features. The max pooling layer outputs feature maps with resolution of
$32/2^{k+1}\times 32/2^{k+1}$
. The pooled features are connected to fully connected layers. Fully connected layers compare pooled features to classify ground truth flow fields into class 1 and predicted flow fields into class 0. The output of each discriminative network is a single continuous scalar between 0 and 1, where an output value larger than a threshold (0.5) is classified into class 1 and an output value smaller than the threshold is classified into class 0. Output neurons of the last fully connected layer of each discriminative network
$D_{k}$
are activated using the sigmoid function to bound the output values within 0 to 1, while other output neurons, including feature maps of convolution layers, are activated with the ReLU activation function.
Note that the number of neurons in the first layer of fully connected layers (see table 2) is a function of the square of the subsampled input resolution (
$32\times 32$
); as a result, parameters to learn are increased in the order of the square of the subsampled input resolution. Training could be inefficient or nearly impossible in a larger input domain size with the equivalent resolution (for example,
$250\times 250$
resolution on the domain size of
$7D\times 7D$
) due to the fully connected layer in the discriminator model depending on computing hardware. On the other hand, parameters in the generator model (fully convolutional architecture with padded convolutions) do not depend on the size and resolution of the subsampled inputs. This enables the generator model to predict flow fields in a larger domain size (
$7D\times 7D$
domain with
$250\times 250$
resolution) compared to the subsampled input domain size (
$0.896D\times 0.896D$
domain with
$32\times 32$
resolution).
Table 2. Configuration of the discriminator model inside the GAN.
Figure 7. Schematic diagram of the discriminator model:
$D_{k}$
indicates the discriminative network which is fed with
$G_{k}({\mathcal{I}})$
and
${\mathcal{G}}_{k}({\mathcal{I}})$
,
$G_{k}({\mathcal{I}})$
indicates the set of predicted flow fields from the generative CNN
$G_{k}$
, while
${\mathcal{G}}_{k}({\mathcal{I}})$
indicates the set of ground truth flow fields.
The generator model is trained with the Adam optimizer, which is known to efficiently train a network, particularly in regression problems (Kingma & Ba Reference Kingma and Ba2014). This optimizer computes individual learning rates, which are updated during training, for different weight parameters in a network. The maximum learning rate of the parameters in the generator model is limited to
$4\times 10^{-5}$
. However, the Adam optimizer is reported to perform worse than a gradient descent method with a constant learning rate for a classification problem using CNNs (Wilson et al.
Reference Wilson, Roelofs, Stern, Srebro and Recht2017). As the discriminator model performs classification using CNNs, the discriminator model is trained with the gradient descent method along with a constant learning rate of
$0.02$
. The same optimization method and learning rate have also been utilized in the discriminator model by Mathieu et al. (Reference Mathieu, Couprie and LeCun2015). Networks are trained up to
$6\times 10^{5}$
iterations with a batch size of 8. Training of networks is observed to be sufficiently converged without overfitting, as shown in figure 21 in § C.1.
3.3 Conservation principles
Let
$\unicode[STIX]{x1D6FA}$
be an arbitrary open, bounded and connected domain in
$\mathbb{R}^{3}$
,
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
be a surface of which an outward unit normal vector can be defined as
$\hat{n}=(n^{1},n^{2},n^{3})$
. Also let
$\unicode[STIX]{x1D70C}(t,\boldsymbol{x})$
be the density,
$\boldsymbol{u}(t,\boldsymbol{x})=(u_{1},u_{2},u_{3})$
be the velocity vector,
$p(t,\boldsymbol{x})$
be the pressure and
$\unicode[STIX]{x1D70F}(t,\boldsymbol{x})$
be the shear stress tensor (
$\unicode[STIX]{x1D70F}_{ij}=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}(\unicode[STIX]{x2202}u_{j}/\unicode[STIX]{x2202}x_{i})$
) of ground truth flow fields as a function of time
$t$
and space
$\boldsymbol{x}\in \mathbb{R}^{3}$
. Then conservation laws for mass and momentum can be written as follows:
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D70C}\,\text{d}V=-\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D70C}u_{j}n^{j}\,\text{d}S & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D70C}u_{i}\,\text{d}V=-\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}(\unicode[STIX]{x1D70C}u_{i})u_{j}n^{j}\,\text{d}S-\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}(p\unicode[STIX]{x1D6FF}_{ij})n^{j}\,\text{d}S+\int _{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D70F}_{ji}n^{j}\,\text{d}S, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker delta. The present study utilizes subsets of three-dimensional data (two-dimensional slices). Therefore, the domain
$\unicode[STIX]{x1D6FA}$
becomes a surface in
$\mathbb{R}^{2}$
and the surface
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$
becomes a line in
$\mathbb{R}^{1}$
. Exact mass and momentum conservation cannot be calculated because derivatives in the spanwise direction are not available in two-dimensional slice data. Instead, conservation principles of mass and momentum in a flow field predicted by deep learning are considered in a form that compares the difference between predicted and ground truth flow fields in a two-dimensional space (
$\mathbb{R}^{2}$
).
Extension of the present deep learning methods to three-dimensional volume flow fields is algorithmically straightforward. However, the increase of the required memory space and the operation counts is significant, making the methods impractical. For example, the memory space and the operation counts for
$32\times 32\times 32$
sized volume flow fields are estimated to be increased by two-orders of magnitude compared to those required for the
$32\times 32$
two-dimensional flow fields.
3.4 Loss functions
For a given set of input and ground truth flow fields, the generator model predicts flow fields that minimize a total loss function, which is a combination of specific loss functions as follows:
$$\begin{eqnarray}\displaystyle {\mathcal{L}}_{generator}=\frac{1}{N\unicode[STIX]{x1D706}_{\sum }}\mathop{\sum }_{k=0}^{N-1}\{\unicode[STIX]{x1D706}_{l2}{\mathcal{L}}_{2}^{k}+\unicode[STIX]{x1D706}_{gdl}{\mathcal{L}}_{gdl}^{k}+\unicode[STIX]{x1D706}_{phy}({\mathcal{L}}_{c}^{k}+{\mathcal{L}}_{mom}^{k})+\unicode[STIX]{x1D706}_{adv}{\mathcal{L}}_{adv}^{G,k}\}, & & \displaystyle\end{eqnarray}$$
where
$N(=\;4)$
is the number of scales of the multi-scale CNN and
$\unicode[STIX]{x1D706}_{\sum }=\unicode[STIX]{x1D706}_{l2}+\unicode[STIX]{x1D706}_{gdl}+\unicode[STIX]{x1D706}_{phy}+\unicode[STIX]{x1D706}_{adv}$
. Contributions of each loss function can be controlled by tuning coefficients
$\unicode[STIX]{x1D706}_{l2}$
,
$\unicode[STIX]{x1D706}_{gdl}$
,
$\unicode[STIX]{x1D706}_{phy}$
, and
$\unicode[STIX]{x1D706}_{adv}$
.
Function
${\mathcal{L}}_{2}^{k}$
minimizes the difference between predicted flow fields and ground truth flow fields (see (A 1)), while
${\mathcal{L}}_{gdl}^{k}$
is applied to sharpen flow fields by directly penalizing gradient differences between predicted flow fields and ground truth flow fields (see (A 2)). Loss functions
${\mathcal{L}}_{2}^{k}$
and
${\mathcal{L}}_{gdl}^{k}$
provide prior information to networks that predicted that flow fields should resemble ground truth flow fields. These loss functions support networks to learn fluid dynamics that resemble the flow field, by extracting features in a supervised manner.
Function
${\mathcal{L}}_{c}$
enables networks to learn mass conservation by minimizing the total absolute sum of differences of mass fluxes in each cell in an
$x$
–
$y$
plane as defined in (A 3). Function
${\mathcal{L}}_{mom}$
enables networks to learn momentum conservation by minimizing the total absolute sum of differences of momentum fluxes due to convection, pressure gradient and shear stress in each cell in an
$x$
–
$y$
plane as defined in (A 4). Loss functions
${\mathcal{L}}_{c}$
and
${\mathcal{L}}_{mom}$
, which are denoted physical loss functions, provide explicit prior information on physical conservation laws to networks, and support networks to extract features including physical conservation laws in a supervised manner. Consideration of conservation of kinetic energy can also be realized using a loss function, but it is not included in the present study since the stability of flow fields predicted by the present networks are not affected by the conservation of kinetic energy.
Function
${\mathcal{L}}_{adv}^{G}$
is a loss function with the purpose of deluding the discriminator model into classifying generated flow fields as ground truth flow fields (see (A 5)). The loss function
${\mathcal{L}}_{adv}^{G}$
provides knowledge in a concealed manner that features of the predicted and the ground truth flow fields should be indistinguishable. This loss function supports networks to extract features of underlying fluid dynamics in an unsupervised manner.
The loss function of the discriminator model is defined as follows:
$$\begin{eqnarray}{\mathcal{L}}_{discriminator}=\frac{1}{N}\mathop{\sum }_{k=0}^{N-1}[L_{bce}(D_{k}({\mathcal{G}}_{k}({\mathcal{I}})),1)+L_{bce}(D_{k}(G_{k}({\mathcal{I}})),0)],\end{eqnarray}$$
where
$L_{bce}$
is the binary cross-entropy loss function defined as
$$\begin{eqnarray}L_{bce}(a,b)=-b\log (a)-(1-b)\log (1-a),\end{eqnarray}$$
for scalar values
$a$
and
$b$
between 0 and 1. Function
${\mathcal{L}}_{discriminator}$
is minimized so that the discriminator model appropriately classifies ground truth flow fields into class 1 and predicted flow fields into class 0. The discriminator model learns flow fields in a low-dimensional feature space.
4 Results
4.1 Comparison of deep learning networks
Four deep learning networks with different combinations of coefficients for loss functions are discussed in the present section. Case A employs a GAN with physical loss functions (
$\unicode[STIX]{x1D706}_{l2}=\unicode[STIX]{x1D706}_{gdl}=1.0$
,
$\unicode[STIX]{x1D706}_{phy}=1.0$
and
$\unicode[STIX]{x1D706}_{adv}=0.1$
); Case B employs a GAN without physical loss functions (
$\unicode[STIX]{x1D706}_{l2}=\unicode[STIX]{x1D706}_{gdl}=1.0$
,
$\unicode[STIX]{x1D706}_{phy}=0$
and
$\unicode[STIX]{x1D706}_{adv}=0.1$
); Case C employs a multi-scale CNN with physical loss functions (
$\unicode[STIX]{x1D706}_{l2}=\unicode[STIX]{x1D706}_{gdl}=1.0$
,
$\unicode[STIX]{x1D706}_{phy}=1.0$
and
$\unicode[STIX]{x1D706}_{adv}=0$
); Case D employs a multi-scale CNN without physical loss functions (
$\unicode[STIX]{x1D706}_{l2}=\unicode[STIX]{x1D706}_{gdl}=1.0$
,
$\unicode[STIX]{x1D706}_{phy}=0$
and
$\unicode[STIX]{x1D706}_{adv}=0$
). See §§ C.2 and C.3 for the determination of the weight parameters
$\unicode[STIX]{x1D706}_{adv}$
and
$\unicode[STIX]{x1D706}_{phy}$
, respectively. All deep learning cases (Cases A–D) are trained with flow fields at
$Re_{D}=300$
and
$500$
, which are in the three-dimensional wake transition regime, and tested on flow fields at
$Re_{D}=150$
(the two-dimensional vortex shedding regime),
$400$
(the same flow regime with training) and
$3900$
(the shear-layer transition regime).
Figure 8. Comparison of the streamwise velocity (
$u/U_{\infty }$
) at
$Re_{D}=3900$
predicted in Cases A–D. (a) Input set; (b) after a single prediction step (
$1\unicode[STIX]{x1D6FF}t$
), and (c) nine more recursive prediction steps (
$10\unicode[STIX]{x1D6FF}t$
). 20 contour levels from
$-$
0.5 to 1.0 are shown. Solid lines and dashed lines indicate positive and negative contour levels, respectively.
Predicted flow fields at
$Re_{D}=3900$
from Cases A–D are shown in figure 8. Flow fields after time steps larger than
$\unicode[STIX]{x1D6FF}t$
are predicted recursively by utilizing flow fields predicted at prior time steps as parts of the input. Flow fields predicted after a single time step (
$1\unicode[STIX]{x1D6FF}t$
) are found to agree well with ground truth flow fields for all deep learning cases, even though the trained networks have not seen such small-scale flow structures at a higher Reynolds number. Note that the time-step size for network prediction
$\unicode[STIX]{x1D6FF}t$
corresponds to 20 times the simulation time-step size. Differences between the predicted and the ground truth flow fields increase as the number of recursive steps increases because errors from the previous predictions are accumulated to the next time-step prediction. Particularly, dissipation of small-scale flow structures in the wake region is observed, while large-scale vortical motions characterizing Kármán vortex shedding are well predicted.
Figure 9. Local distributions of errors for
$u/U_{\infty }$
after a single prediction step at (a)
$Re_{D}=150$
(10 contour levels from 0 to 0.04), (b)
$Re_{D}=400$
(10 contour levels from 0 to 0.04) and (c)
$Re_{D}=3900$
(10 contour levels from 0.0 to 0.33). Locations of
$L_{\infty }$
,
${L_{c}}_{\infty }$
(maximum error in mass conservation) and
${L_{mom}}_{\infty }$
(maximum error in momentum conservation) are indicated by ○, ♢ and ▫, respectively.
Figure 10. Comparisons of (a)
$L_{2}$
, (b)
$L_{\infty }$
, (c)
$L_{c}$
and (d)
$L_{mom}$
errors for Cases A–D. See appendix B for definitions of the errors. The time-step interval between flow fields is
$\unicode[STIX]{x1D6FF}t=20\unicode[STIX]{x0394}tU_{\infty }/D=0.1$
. ○ and solid line: Case A; ▫ and dashed line: Case B; ▵ and dash-dotted line: Case C; ▹ and dotted line: Case D.
Local distributions of errors for the streamwise velocity after a single time step for four deep learning cases are compared in figure 9, while global errors such as
$L_{2}$
,
$L_{\infty }$
,
$L_{c}$
and
$L_{mom}$
as a function of the recursive time step are compared in figure 10. See appendix B for definitions of errors. All networks show that the maximum errors are located in accelerating boundary layers on the cylinder wall or in the braid region in the wake. Steep velocity gradients captured with relatively coarse resolution in the deep learning prediction are considered as the cause for relatively high errors in accelerating boundary layers. Magnitudes of the maximum errors at
$Re_{D}=400$
are found to be smaller (see figure 9
b) than those at
$Re_{D}=150$
(figure 9
a) and
$3900$
(figure 9
c). This result implies that a network performs best in predicting flow fields in a regime that has been utilized during training, while the network shows relatively large errors in predicting flow fields in the flow regime with higher complexity.
Interestingly, unlike errors at
$1\unicode[STIX]{x1D6FF}t$
, as the recursive prediction step advances, errors at
$Re_{D}=150$
are observed to increase more slowly than those at
$Re_{D}=400$
(see figure 10). This implies that deep learning networks are capable of effectively learning large-scale or mainly two-dimensional vortex shedding physics from flow in three-dimensional wake transition regimes (
$Re_{D}=300$
and
$500$
), thereby accurately predicting two-dimensional vortex shedding at
$Re_{D}=150$
, flow fields of which are not included in the training dataset.
As also shown in figure 10, the multi-scale CNN with physical loss functions (Case C) shows reduction of
$L_{c}$
and
$L_{mom}$
errors, during recursive prediction steps, compared to the multi-scale CNN without physical loss functions (Case D), indicating the advantage of the incorporation of physical loss functions in improving the conservation of mass and momentum. At the same time, however,
$L_{2}$
and
$L_{\infty }$
errors at
$Re_{D}=400$
and
$3900$
are found to increase in Cases C and D. Case A, which employs the GAN with physical loss functions, shows similar error trends to Case C but with smaller magnitudes of the
$L_{\infty }$
error at
$Re_{D}=150$
.
On the other hand, the GAN without physical loss functions (Case B) shows smaller
$L_{2}$
and
$L_{mom}$
errors for all three Reynolds number cases than those in Case D which employs the multi-scale CNN without physical loss functions. The
$L_{\infty }$
errors in Case B at
$Re_{D}=150$
and
$400$
are also significantly smaller than those in Case D. These results imply that GANs (with and without physical loss functions, Cases A and B) and the multi-scale CNN with physical loss functions (Case C) are more capable of extracting features related to unsteady vortex shedding physics over a circular cylinder than the multi-scale CNN without physical loss functions (Case D). The GAN without physical loss function (Case B) is found to consistently reduce errors associated with resemblance (
$L_{2}$
and
$L_{\infty }$
) while error behaviours associated with conservation loss functions are rather inconsistent. Effects of physical loss functions on reduction of conservation errors are identifiable for networks with physical loss functions (Cases A and C).
Vortical structures at each Reynolds number predicted by the present four deep learning networks appear to be similar to each other after a single prediction step as shown in figure 11(a). However, all deep learning cases have difficulties in learning the production of small-scale vortical structures. At
$10\unicode[STIX]{x1D6FF}t$
, small-scale vortical structures, which are not present in the ground truth flow field, are found to be generated inside shed large-scale vortices at
$Re_{D}=150$
, while many small-scale vortices are missed in the wake at
$Re_{D}=3900$
(figure 11
b). This observation implies that a network has difficulty in predicting flow fields, especially in recursive predictions as errors from previous predictions are accumulated, in flow regimes which are different from the regime for training.
After a few recursive prediction steps, Case D, where the multi-scale CNN without physical loss functions is applied, shows unphysical vortical structures near the front stagnation point, which are not present in flow fields predicted by other cases at the three considered Reynolds numbers (figure 11 b). The effect of the inaccurate prediction in Case D on errors also appears in figure 10, where magnitudes are larger than those in Cases A, B and C.
All deep learning cases are found to be capable of predicting future flow fields, particularly in single-step predictions. However, networks with additional consideration of physics in either a supervised or an unsupervised manner (Cases A–C) are recommended for predicting further future flow fields with many recursive steps. Especially, the GAN without physical loss functions (Case B) is found to be the best among the considered networks for minimizing
$L_{2}$
and
$L_{\infty }$
errors (see figure 10) while also satisfying the conservation of mass and momentum favorably.
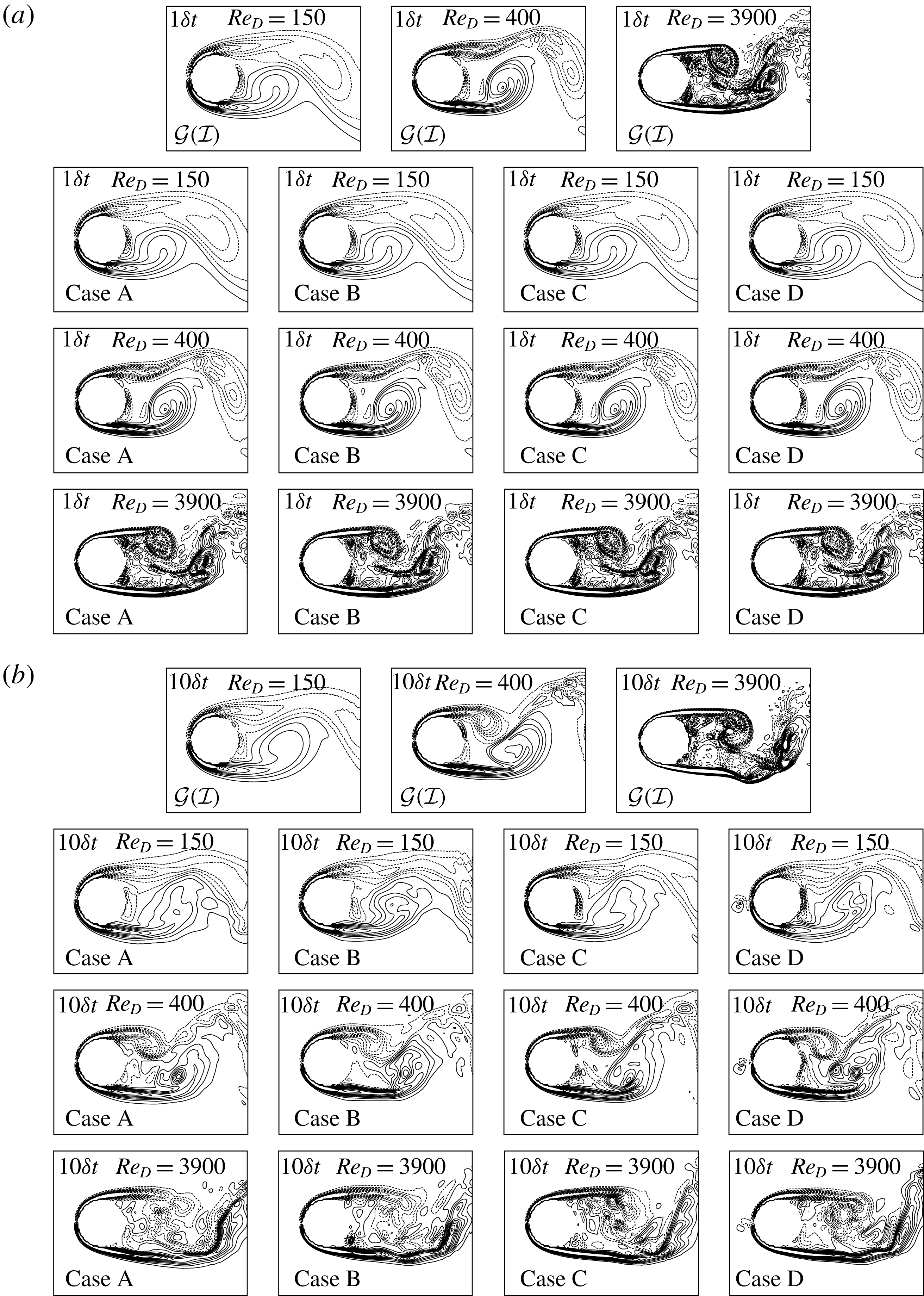
Figure 11. Comparison of the spanwise vorticity after (a) a single prediction step (
$1\unicode[STIX]{x1D6FF}t$
) and (b) nine more recursive prediction steps (
$10\unicode[STIX]{x1D6FF}t$
). 20 contour levels from
$-$
10.0 to 10.0 are shown. Solid lines and dashed lines indicate positive and negative contour levels, respectively.
4.2 Analysis on captured and missed flow physics
Discussion in the present section is focused on the GAN without physical loss functions (Case B), which is trained with flow fields at
$Re_{D}=300$
and
$500$
(the three-dimensional wake transition regime) and tested on flow fields at
$Re_{D}=150$
(the two-dimensional vortex shedding regime),
$400$
(the same flow regime with training) and
$3900$
(the shear-layer transition regime), in order to assess what flow characteristics the network captures or misses.
Figure 12. Contours of the spanwise vorticity calculated using ground truth velocity fields (
${\mathcal{G}}({\mathcal{I}})$
) and velocity fields predicted by the GAN (
$G({\mathcal{I}})$
) after (a) a single prediction step (
$1\unicode[STIX]{x1D6FF}t$
) and (b) nine more recursive prediction steps (
$10\unicode[STIX]{x1D6FF}t$
) at
$Re_{D}=150$
,
$400$
and
$3900$
. 20 contour levels from
$-$
10.0 to 10.0 are shown. Solid lines and dashed lines indicate positive and negative contour levels, respectively.
Contour plots of the spanwise vorticity calculated using ground truth velocity fields and velocity fields predicted by the GAN are compared in figure 12 for three Reynolds numbers at
$1\unicode[STIX]{x1D6FF}t$
and
$10\unicode[STIX]{x1D6FF}t$
. First of all, laminar flow at the frontal face of the cylinder as well as the separated laminar shear layers including lengthening of the shear layers and detachment from the wall are observed to be well captured in all three Reynolds number cases. Convection (downstream translation) and diffusion of overall large-scale vortical structures in the wake are also well predicted at both
$1\unicode[STIX]{x1D6FF}t$
and
$10\unicode[STIX]{x1D6FF}t$
. However, as also mentioned in the previous section, prediction results show differences in the generation and dissipation of small-scale vortices. After a number of recursive prediction steps, along with the non-zero spanwise velocity, unexpected smaller scale vortices than those present in the ground truth flow field are generated at
$Re_{D}=150$
, in which Reynolds number regime, downstream vortical structures are expected to be laminar and two-dimensional. Generation of smaller scale vortical structures than those in ground truth flow fields after a few recursive predictions is also noticed in the GAN prediction at
$Re_{D}=400$
. On the other hand, it is found that the GAN fails to accurately predict small-scale vortical structures inside large-scale vortices at
$Re_{D}=3900$
. It is thought that the present results imply that the GAN is not fully trained for predicting production and dissipation of small-scale vortices. The lack of flow information along the spanwise direction is considered as a major cause for this failure. Due to the reason mentioned in § 3.3, the spanwise information in the present training dataset includes only the spanwise velocity on a two-dimensional sliced domain, and therefore misses variation of flow variables along the spanwise direction.
The lack of spanwise information on flow variables seems to lead the network to miss the mechanism for generation of small-scale vortices, which can be formulated as the vortex stretching term in the spanwise vorticity (
$\unicode[STIX]{x1D714}_{z}$
) equation. The stretching term
$\unicode[STIX]{x1D714}_{z}(\unicode[STIX]{x2202}w/\unicode[STIX]{x2202}z)$
, which is associated with the generation of small-scale vortices, is missed in the present training. On the other hand, convection and diffusion of the spanwise vorticity are dominated by
$u(\unicode[STIX]{x2202}\unicode[STIX]{x1D714}_{z}/\unicode[STIX]{x2202}x)+v(\unicode[STIX]{x2202}\unicode[STIX]{x1D714}_{z}/\unicode[STIX]{x2202}y)$
and
$(1/Re_{D})(\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}_{z}/\unicode[STIX]{x2202}x\unicode[STIX]{x2202}x+\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D714}_{z}/\unicode[STIX]{x2202}y\unicode[STIX]{x2202}y)$
, which can be rather easily trained using the given flow field data.
Figure 13. Profiles of the streamwise velocity at three streamwise locations after (a) a single prediction step (
$1\unicode[STIX]{x1D6FF}t$
) and (b) nine more recursive prediction steps (
$10\unicode[STIX]{x1D6FF}t$
) at
$Re_{D}=150$
, 400 and
$3900$
. Circles indicate ground truth results and solid lines indicate results predicted by the GAN. Profiles at
$x/D=1.0$
and 2.0 are shifted by
$-$
1.7 and
$-$
3.4 in the vertical axis, respectively.
Convection and diffusion phenomena in flow around a cylinder are investigated more quantitatively in the development of the velocity deficit. Profiles of the streamwise velocity from ground truth flow fields (○) and flow fields predicted by the GAN (solid lines) at three streamwise locations,
$x/D=0$
,
$1.0$
and
$2.0$
, are compared in figure 13. Velocity profiles at
$x/D=0$
show no identifiable differences between ground truth and GAN flow fields at both
$1\unicode[STIX]{x1D6FF}t$
and
$10\unicode[STIX]{x1D6FF}t$
at all Reynolds numbers (
$Re_{D}=150$
,
$400$
and
$3900$
). This is because flow at
$x/D=0$
is laminar two-dimensional boundary layer flow, the characteristics of which are rather easily trained by the network. Noticeable differences in the velocity deficit are observed in the comparison at
$10\unicode[STIX]{x1D6FF}t$
in the wake region,
$x/D=2.0$
, at
$Re_{D}=3900$
, where small-scale oscillatory motions are not accurately captured by the GAN. Recursively predicted velocity deficits at
$Re_{D}=150$
and
$400$
are in good agreement with the ground truth velocity deficit in terms of the peak, width and shape at both streamwise locations.
Figure 14. Power spectral density of the streamwise velocity at
$x/D=2.0$
after (a) a single prediction step (
$1\unicode[STIX]{x1D6FF}t$
) and (b) nine more recursive prediction steps (
$10\unicode[STIX]{x1D6FF}t$
) at
$Re_{D}=150$
, 400 and
$3900$
. Circles indicate ground truth results and solid lines indicate results predicted by the GAN.
Plots of the power spectral density (PSD) of the streamwise velocity along the vertical axis (
$y$
) in the wake region at
$x/D=2.0$
are shown in figure 14 to evaluate the wavenumber content of wake flow. At
$Re_{D}=150$
and
$400$
, PSDs produced by the GAN show good agreement with ground truth results in the single-step prediction (
$1\unicode[STIX]{x1D6FF}t$
), and are found to be still close to ground truth PSDs with marginal deviations in the middle- to high-wavenumber contents (
$k>10$
) after nine recursive predictions. On the other hand, PSDs produced by the GAN at
$Re_{D}=3900$
at both
$1\unicode[STIX]{x1D6FF}t$
and
$10\unicode[STIX]{x1D6FF}t$
show deviations from ground truth PSDs, especially for high-wavenumber contents, again indicating the difficulty in learning the mechanism for production of small-scale vortices (high wavenumbers).
Figure 15. Local distributions of errors for
$u/U_{\infty }$
after a single prediction step at
$Re_{D}=3900$
(10 contour levels from 0.0 to 0.33). Locations of
$L_{\infty }$
,
${L_{c}}_{\infty }$
(maximum error in mass conservation) and
${L_{mom}}_{\infty }$
(maximum error in momentum conservation) are indicated by ○, ♢ and ▫, respectively.
4.3 Training with additional data
The GAN without physical loss functions is trained with additional flow field data at Reynolds numbers of
$1000$
and
$3000$
, in order to investigate the effect of small-scale contents in training data on the prediction of small-scale vortical motions in flow in the shear-layer transition regime (
$Re_{D}=3900$
). Local distributions of errors for the streamwise velocity after a single time step for the GAN and the GAN with additional flow field data are compared in figure 15. Magnitudes of maximum errors, especially the mass and momentum errors, are significantly reduced by training the network with flow fields in the same flow regime as that to be predicted. Nevertheless, maximum errors are still larger than those at low Reynolds numbers (see figure 9
a,b). The lack of spanwise information in the input is considered to be the remaining cause for the errors.
Figure 16. Contour plots of the spanwise vorticity calculated using ground truth velocity fields and velocity fields predicted by the GANs at
$Re_{D}=3900$
after (a)
$1\unicode[STIX]{x1D6FF}t$
and (b)
$10\unicode[STIX]{x1D6FF}t$
. Solid lines and dashed lines denote positive and negative contour levels, respectively. (c) Plots of the power spectral density at
$1\unicode[STIX]{x1D6FF}t$
and
$10\unicode[STIX]{x1D6FF}t$
. 20 contour levels from
$-$
10.0 to 10.0 are shown. Circles indicate ground truth result, while the dashed line and the solid line correspond to predicted results using the GAN and the GAN with additional data, respectively.
Contours of the spanwise vorticity calculated by ground truth flow fields, flow fields predicted by the GAN trained with data at
$Re_{D}=300$
and
$500$
and flow fields predicted by the GAN trained with additional data at
$Re_{D}=1000$
and
$3000$
are compared in figure 16(a,b). Training with additional data in the same flow regime is found to clearly improve the prediction of small-scale motions after a single prediction step (
$1\unicode[STIX]{x1D6FF}t$
). The spanwise vorticity predicted by the GAN trained with additional data is found to agree much better with the ground truth vorticity than that predicted by the GAN trained with flow fields only at
$Re_{D}=300$
and
$500$
after nine more recursive prediction steps (
$10\unicode[STIX]{x1D6FF}t$
) as shown in figure 16(b). However, as discussed in the previous section (§ 4.2), the GAN trained with additional data also suffers from a lack of production of small-scale vortical structures. PSDs produced by the GAN trained for
$Re_{D}=300$
and
$500$
and the GAN trained with additional data are close to the ground truth PSD at
$1\unicode[STIX]{x1D6FF}t$
, while the GAN trained with additional data better predicts small-scale high-wavenumber contents. Differences among predicted and ground truth PSDs become larger at
$10\unicode[STIX]{x1D6FF}t$
, where reduced small-scale high-wavenumber contents are clearly observable for both GANs (figure 16
c).
4.4 Training with a large time-step interval
To investigate the potential of using a GAN in practical applications, where predicting large-scale flow motions is important, the GAN without physical loss functions is trained with a large time-step interval of
$25\unicode[STIX]{x1D6FF}t=500\unicode[STIX]{x0394}tU_{\infty }/D=2.5$
. This time-step interval is 25 times larger than the previous deep learning time-step interval and 500 times larger than the simulation time-step interval. Figure 17 shows plots of two-point correlations of the streamwise velocity along the
$y$
direction, which provide information on the large-scale fluid motions at three downstream wake locations at
$Re_{D}=3900$
. After a single step with
$25\unicode[STIX]{x1D6FF}t$
, it is found that two-point correlations predicted by the GAN are in good agreement with correlations of the ground truth flow field. After four additional recursive large steps (
$125\unicode[STIX]{x1D6FF}t$
), however, small deviations of correlations from ground truth results are observed in the downstream wake region (
$x/D=3.0$
). Note that
$125\unicode[STIX]{x1D6FF}t$
corresponds to
$2500$
time steps of the numerical simulation conducted for the ground truth flow field.
Figure 17. Two-point correlations of the streamwise velocity at three downstream locations (
$x/D=1.0$
,
$2.0$
and
$3.0$
) at
$Re_{D}=3900$
. Circles indicate ground truth results and solid lines indicate predicted results by the GAN. Two-point correlations at
$x/D=2.0$
and
$3.0$
are shifted by
$-$
1 and
$-$
2 along the vertical axis, respectively.
Contour plots of the streamwise velocity predicted by the GAN at
$Re_{D}=3900$
are shown in figure 18 (see figures 28–30 in appendix E for contour plots of the other flow variables). Flow fields at
$50\unicode[STIX]{x1D6FF}t$
,
$75\unicode[STIX]{x1D6FF}t$
,
$100\unicode[STIX]{x1D6FF}t$
and
$125\unicode[STIX]{x1D6FF}t$
are recursively predicted. As shown in figure 18, large-scale oscillations of the streamwise velocity behind the cylinder are well predicted, while small-scale flow structures are found to be rather rapidly dissipated compared to those in ground truth flow fields. This may be partly due to the dynamics of small-scale flow structures, the time scales (
$\unicode[STIX]{x1D70F}$
) of which are smaller than the training interval size (
$t=nD/U_{\infty }\unicode[STIX]{x1D6FF}t$
, where
$n$
is an integer), and are disregarded from input information. The time scale of a small-scale flow structure can be approximated as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}\sim \left(\frac{\unicode[STIX]{x1D708}}{\unicode[STIX]{x1D716}}\right)^{1/2} & & \displaystyle\end{eqnarray}$$
according to Tennekes & Lumley (Reference Tennekes and Lumley1972), where
$\unicode[STIX]{x1D708}$
is the kinematic viscosity and
$\unicode[STIX]{x1D716}$
is the dissipation rate per unit mass that is approximated as
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}\sim \frac{u^{3}}{l}\sim \frac{U_{\infty }^{3}}{D}, & & \displaystyle\end{eqnarray}$$
where
$u$
is the velocity scale and
$l$
is the length scale of a large-scale flow motion. The ratio of the time-scale for a small-scale flow structure to the training interval size can be derived as follows:
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D70F}}{t}\sim \frac{\unicode[STIX]{x1D70F}U_{\infty }}{nD\unicode[STIX]{x1D6FF}t}\sim \frac{1}{n\unicode[STIX]{x1D6FF}t}\left(\frac{U_{\infty }D}{\unicode[STIX]{x1D708}}\right)^{-1/2}=\frac{1}{n\unicode[STIX]{x1D6FF}t\sqrt{Re_{D}}}. & & \displaystyle\end{eqnarray}$$
The ratio of the time scale for a small-scale flow structure to the training interval size decreases as the Reynolds number and the integer
$n$
increase. Therefore, small-scale flow structures are reasonably well captured by the network trained with a small training-step interval (see figures 24–27), while it is found that small-scale flow structures predicted by the network trained with a large training-step interval of
$25\unicode[STIX]{x1D6FF}t$
, rapidly disappear in the wake (see figures 18, 28–30).
Figure 18. Contour plots of the streamwise velocity (
$u/U_{\infty }$
) at
$Re_{D}=3900$
after
$25\unicode[STIX]{x1D6FF}t$
,
$50\unicode[STIX]{x1D6FF}t$
,
$75\unicode[STIX]{x1D6FF}t$
,
$100\unicode[STIX]{x1D6FF}t$
and
$125\unicode[STIX]{x1D6FF}t$
, where
$1\unicode[STIX]{x1D6FF}t=20\unicode[STIX]{x0394}tU_{\infty }/D=0.1$
. Flow fields at
$50\unicode[STIX]{x1D6FF}t$
,
$75\unicode[STIX]{x1D6FF}t$
,
$100\unicode[STIX]{x1D6FF}t$
and
$125\unicode[STIX]{x1D6FF}t$
are recursively predicted (utilizing flow fields predicted from prior time steps as part of the input). (a) Input set, (b) ground truth flow fields and (c) flow fields predicted by the GAN. 20 contour levels from
$-$
0.5 to 1.0 are shown. Solid lines and dashed lines indicate positive and negative contour levels, respectively.
Regardless of the rapid loss of small-scale flow structures in the wake, flow fields predicted after a single large prediction-step interval of
$25\unicode[STIX]{x1D6FF}t$
exhibit lower errors compared to flow fields recursively predicted at 25 small prediction steps of
$25\times 1\unicode[STIX]{x1D6FF}t$
(see table 3). The reduction of errors implies that predicting with a network trained with a large time-step interval enables the network to focus more on energetic large-scale flow motions by disregarding small-scale flow motions.
Table 3. Comparison of errors for each flow variable at
$Re_{D}=3900$
from predictions obtained after 25 small time-step intervals of
$1\unicode[STIX]{x1D6FF}t$
and after a single large time-step interval of
$25\unicode[STIX]{x1D6FF}t$
.
$1\unicode[STIX]{x1D6FF}t=20\unicode[STIX]{x0394}tU_{\infty }/D=0.1$
. Errors are composed of the mean and standard deviations determined by 32 independent prediction results.
5 Conclusion
Unsteady flow fields around a circular cylinder at Reynolds numbers that were not informed during training were predicted using deep learning techniques. Datasets of flow fields have been constructed using numerical simulations in three different flow regimes: a two-dimensional laminar vortex shedding regime, a three-dimensional wake transition regime and a shear-layer transition regime. The present deep learning techniques are found to well predict convection and diffusion of large-scale vortical structures, while the mechanism for production of small-scale vortical structures is difficult to account for. Depending on the training scheme, the present deep learning techniques are found also to be capable of successfully predicting large-scale flow motions with large time-step interval sizes, which can be two to three orders of magnitude larger than the time-step interval size for the conventional unsteady numerical simulations. Predictions using the present deep learning networks can be conducted with significantly lower computational cost than numerical simulations regardless of the Reynolds number. A wall-clock time of 0.3 s is required for a time-step advance using a single graphic processing unit (NVIDIA Titan Xp).
Four deep learning networks, GANs with and without physical loss functions and multi-scale CNNs with and without physical loss functions, have been trained and compared for their predictive performance. The physical loss functions proposed in the present study inform the networks with, explicitly, the conservation of mass and momentum. Adversarial training in the GAN allows the deep learning network to extract various flow features in an unsupervised manner. All four deep learning techniques are shown to be capable of predicting flow fields in the immediate future. However, for long-term prediction using a recursive technique, which employs the predicted flow fields as part of the input dataset, GANs and the multi-scale CNN with physical loss functions are shown to be better predictors than the multi-scale CNN without physical loss functions. It has been found that the GAN without physical loss functions is the best at achieving a good resemblance to the ground truth flow field during recursive predictions. Especially, GAN-based networks take advantage of unsupervised training, so they can be applied to problems where underlying physics is unknown a priori. The present deep learning methods are expected to be useful in many practical applications, such as real-time flow control and guidance of aero- or hydro-vehicles, fast weather forecasting, etc., where fast prediction of energetic large-scale flow motions is important.
Physical interpretability of deep learning techniques is still an open problem and, therefore, further research is necessary to enhance our understanding of the underlying mechanisms of deep learning networks for prediction of fluid flow, especially in transitional and turbulent flow regimes.
Acknowledgements
This work was supported by the Samsung Research Funding Center of Samsung Electronics under Project Number SRFC-TB1703-01 and National Research Foundation of Korea (NRF) under grant no. NRF-2017R1E1A 1A03070514.
Appendix A. Loss functions
Function
${\mathcal{L}}_{2}^{k}$
minimizes the difference between the predicted and the ground truth flow fields as follows:
$$\begin{eqnarray}{\mathcal{L}}_{2}^{k}=\Vert G_{k}({\mathcal{I}})-{\mathcal{G}}_{k}({\mathcal{I}})\Vert _{2}^{2}.\end{eqnarray}$$
Also,
${\mathcal{L}}_{gdl}^{k}$
is a second-order central-difference version of the gradient difference loss function proposed by Mathieu et al. (Reference Mathieu, Couprie and LeCun2015), which is applied to sharpen flow fields by directly penalizing gradient differences between the predicted and the ground truth flow fields as follows:
$$\begin{eqnarray}\displaystyle {\mathcal{L}}_{gdl}^{k} & = & \displaystyle \mathop{\sum }_{i}\mathop{\sum }_{j}\left|\left|\frac{({\mathcal{G}}_{k}({\mathcal{I}})_{(i+1,j)}-{\mathcal{G}}_{k}({\mathcal{I}})_{(i-1,j)})}{2}\right|-\left|\frac{(G_{k}({\mathcal{I}})_{(i+1,j)}-G_{k}({\mathcal{I}})_{(i-1,j)})}{2}\right|\right|\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{i}\mathop{\sum }_{j}\left|\left|\frac{({\mathcal{G}}_{k}({\mathcal{I}})_{(i,j+1)}-{\mathcal{G}}_{k}({\mathcal{I}})_{(i,j-1)})}{2}\right|-\left|\frac{(G_{k}({\mathcal{I}})_{(i,j+1)}-G_{k}({\mathcal{I}})_{(i,j-1)})}{2}\right|\right|,\qquad\end{eqnarray}$$
where the subscript
$(i,j)$
indicates grid indices in the discretized flow domain, and
$n_{x}$
and
$n_{y}$
indicate the number of grid cells in the
$x$
and
$y$
directions, respectively.
Let
$u^{k}$
,
$v^{k}$
,
$w^{k}$
and
$p^{k}$
be non-dimensionalized flow variables retrieved from ground truth flow fields (
${\mathcal{G}}_{k}({\mathcal{I}})$
) and
$\widetilde{u}^{k}$
,
$\widetilde{v}^{k}$
,
$\widetilde{w}^{k}$
and
$\widetilde{p}^{k}$
be non-dimensionalized flow variables retrieved from predicted flow fields (
$G_{k}({\mathcal{I}})$
). Flow variables on the right, left, top and bottom cell surfaces are calculated by the arithmetic mean between two neighbouring cells as
$\unicode[STIX]{x1D719}_{r}=\frac{1}{2}(\unicode[STIX]{x1D719}_{(i,j)}+\unicode[STIX]{x1D719}_{(i+1,j)})$
,
$\unicode[STIX]{x1D719}_{l}=\frac{1}{2}(\unicode[STIX]{x1D719}_{(i,j)}+\unicode[STIX]{x1D719}_{(i-1,j)})$
,
$\unicode[STIX]{x1D719}_{t}=\frac{1}{2}(\unicode[STIX]{x1D719}_{(i,j)}+\unicode[STIX]{x1D719}_{(i,j+1)})$
and
$\unicode[STIX]{x1D719}_{b}=\frac{1}{2}(\unicode[STIX]{x1D719}_{(i,j)}+\unicode[STIX]{x1D719}_{(i,j-1)})$
for a variable
$\unicode[STIX]{x1D719}$
which is a function of the grid index (
$i$
,
$j$
). Function
${\mathcal{L}}_{c}$
enables networks to learn mass conservation by minimizing the total absolute sum of mass flux differences in each cell in an
$x$
–
$y$
plane as follows:
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x0394}\text{Con.}_{(i,j)}^{k}=|(u_{r}^{k}-u_{l}^{k})-(\widetilde{u}_{r}^{k}-\widetilde{u}_{l}^{k})|+|(v_{t}^{k}-v_{b}^{k})-(\widetilde{v}_{t}^{k}-\widetilde{v}_{b}^{k})|,\\ \displaystyle {\mathcal{L}}_{c}^{k}=\mathop{\sum }_{i}\mathop{\sum }_{j}\unicode[STIX]{x0394}\text{Con.}_{(i,j)}^{k}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Function
${\mathcal{L}}_{mom}$
enables networks to learn momentum conservation by minimizing the total absolute sum of differences of momentum fluxes due to convection, pressure gradient and shear stress in each cell in an
$x$
–
$y$
plane as follows:
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}rcl@{}}\displaystyle \unicode[STIX]{x0394}\text{Mom.}_{(i,j)}^{k}\; & =\; & |((u_{r}^{k})^{2}-(u_{l}^{k})^{2})-((\widetilde{u}_{r}^{k})^{2}-(\widetilde{u}_{l}^{k})^{2})|+|(u_{r}^{k}v_{r}^{k}-u_{l}^{k}v_{l}^{k})-(\widetilde{u}_{r}^{k}\widetilde{v}_{r}^{k}-\widetilde{u}_{l}^{k}\widetilde{v}_{l}^{k})|\\ \displaystyle \; & \; & +\,|((v_{t}^{k})^{2}-(v_{b}^{k})^{2})-((\widetilde{v}_{t}^{k})^{2}-(\widetilde{v}_{b}^{k})^{2})|+|(v_{t}^{k}u_{t}^{k}-v_{b}^{k}u_{b}^{k})-(\widetilde{v}_{t}^{k}\widetilde{u}_{t}^{k}-\widetilde{v}_{b}^{k}\widetilde{u}_{b}^{k})|\\ \displaystyle \; & \; & +\,|(p_{r}^{k}-p_{l}^{k})-(\widetilde{p}_{r}^{k}-\widetilde{p}_{l}^{k})|+|(p_{t}^{k}-p_{b}^{k})-(\widetilde{p}_{t}^{k}-\widetilde{p}_{b}^{k})|\\ \; & \; & +\,\displaystyle \frac{1}{Re_{D}}\left\{\left|\left(\frac{v_{(i+1,j)}^{k}-2v_{(i,j)}^{k}+v_{(i-1,j)}^{k}}{\unicode[STIX]{x1D6E5}_{x}}\right)-\left(\frac{\widetilde{v}_{(i+1,j)}^{k}-2\widetilde{v}_{(i,j)}^{k}+\widetilde{v}_{(i-1,j)}^{k}}{\unicode[STIX]{x1D6E5}_{x}}\right)\right|\right.\\ \; & \; & +\displaystyle \left|\left(\frac{v_{(i,j+1)}^{k}-2v_{(i,j)}^{k}+v_{(i,j-1)}^{k}}{\unicode[STIX]{x1D6E5}_{y}}\right)-\left(\frac{\widetilde{v}_{(i,j+1)}^{k}-2\widetilde{v}_{(i,j)}^{k}+\widetilde{v}_{(i,j-1)}^{k}}{\unicode[STIX]{x1D6E5}_{y}}\right)\right|\\ \; & \; & +\displaystyle \left|\left(\frac{u_{(i,j+1)}^{k}-2u_{(i,j)}^{k}+u_{(i,j-1)}^{k}}{\unicode[STIX]{x1D6E5}_{y}}\right)-\left(\frac{\widetilde{u}_{(i,j+1)}^{k}-2\widetilde{u}_{(i,j)}^{k}+\widetilde{u}_{(i,j-1)}^{k}}{\unicode[STIX]{x1D6E5}_{y}}\right)\right|\\ \; & \; & \left.+\displaystyle \left|\left(\frac{u_{(i+1,j)}^{k}-2u_{(i,j)}^{k}+u_{(i-1,j)}^{k}}{\unicode[STIX]{x1D6E5}_{x}}\right)-\left(\frac{\widetilde{u}_{(i+1,j)}^{k}-2\widetilde{u}_{(i,j)}^{k}+\widetilde{u}_{(i-1,j)}^{k}}{\unicode[STIX]{x1D6E5}_{x}}\right)\right|\right\},\\ {\mathcal{L}}_{mom}^{k}\; & =\; & \displaystyle \mathop{\sum }_{i}\mathop{\sum }_{j}\unicode[STIX]{x0394}\text{Mom.}_{(i,j)}^{k},\end{array}\right\} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D6E5}_{x}$
and
$\unicode[STIX]{x1D6E5}_{y}$
are grid spacings in the
$x$
and
$y$
directions, respectively.
Function
${\mathcal{L}}_{adv}^{G}$
is a loss function with the purpose of deluding the discriminator model to classify generated flow fields as class 1 as follows:
$$\begin{eqnarray}{\mathcal{L}}_{adv}^{G}=L_{bce}(D_{k}(G_{k}({\mathcal{I}})),1).\end{eqnarray}$$
Appendix B. Error functions
Let
$u$
,
$v$
,
$w$
and
$p$
be non-dimensionalized flow variables retrieved from ground truth flow fields and
$\widetilde{u}$
,
$\widetilde{v}$
,
$\widetilde{w}$
and
$\widetilde{p}$
be non-dimensionalized flow variables retrieved from predicted flow fields. Error functions are defined as follows:
$$\begin{eqnarray}\displaystyle L_{2} & = & \displaystyle \left(\frac{1}{4n_{x}n_{y}}\mathop{\sum }_{i}\mathop{\sum }_{j}\{(u_{(i,j)}-\widetilde{u}_{(i,j)})^{2}+(v_{(i,j)}-\widetilde{v}_{(i,j)})^{2}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\vphantom{\frac{1}{4n_{x}n_{y}}\mathop{\sum }_{j}}(w_{(i,j)}-\widetilde{w}_{(i,j)})^{2}+(p_{(i,j)}-\widetilde{p}_{(i,j)})^{2}\!\}\right)^{1/2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L_{\infty } & = & \displaystyle \frac{1}{4}\left(\max _{i,j}|u_{(i,j)}-\widetilde{u}_{(i,j)}|+\max _{i,j}|v_{(i,j)}-\widetilde{v}_{(i,j)}|\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\max _{i,j}|w_{(i,j)}-\widetilde{w}_{(i,j)}|+\max _{i,j}|p_{(i,j)}-\widetilde{p}_{(i,j)}|\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L_{c} & = & \displaystyle \frac{1}{n_{x}n_{y}}\mathop{\sum }_{i}\mathop{\sum }_{j}\unicode[STIX]{x0394}\text{Con.}_{(i,j)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L_{mom} & = & \displaystyle \frac{1}{n_{x}n_{y}}\mathop{\sum }_{i}\mathop{\sum }_{j}\unicode[STIX]{x0394}\text{Mom.}_{(i,j)},\end{eqnarray}$$
where
$\unicode[STIX]{x0394}\text{Con.}_{(i,j)}$
and
$\unicode[STIX]{x0394}\text{Mom.}_{(i,j)}$
are defined in equations (A 3) and (A 4), respectively.
The present loss functions and error functions for conservation of mass and momentum are not identical to the original forms of conservation laws, but are formulated using the triangle inequality. Therefore, the minimization of the present physical loss functions satisfies conservation of mass and momentum more strictly. In fact, smaller errors are calculated using the original forms of conservation laws, while the errors behave similarly to
$L_{c}$
and
$L_{mom}$
as a function of
$\unicode[STIX]{x1D6FF}t$
.
Appendix C. Parameter study
C.1 Effects of numbers of layers and feature maps
Table 4. Configurations (
$GM_{16}$
,
$GM_{18}$
and
$GM_{20}$
) and number sets (
$N_{32}$
,
$N_{64}$
and
$N_{128}$
) of generator models used in the parameter study.
Errors as a function of the number of convolution layers of the generator model are calculated by training three generator models with configurations of
$GM_{16}$
,
$GM_{18}$
and
$GM_{20}$
with the number set of
$N_{128}$
(see table 4 for these configurations), while errors as a function of the number of feature maps of the generator model in multi-scale CNNs are calculated by training the generator model with number sets
$N_{32}$
,
$N_{64}$
and
$N_{128}$
with the configuration of
$GM_{20}$
. All networks are trained with flow fields at
$Re_{D}=300$
and
$500$
. Magnitudes of errors in configurations considered in the present study are found not to be reduced monotonically with the increase of numbers of layers and feature maps. The configuration with the largest number of convolution layers (
$GM_{20}$
) tends to show smaller
$L_{2}$
and
$L_{\infty }$
errors, while showing
$L_{c}$
and
$L_{mom}$
errors of magnitudes similar to or smaller than those in configurations with smaller numbers of convolution layers (
$GM_{16}$
and
$GM_{18}$
) (figure 19).
The generator model with the largest number set
$N_{128}$
tends to show smaller errors (except for the
$L_{mom}$
error at
$Re_{D}=150$
) on recursive prediction steps compared to smaller number set models (
$N_{32}$
and
$N_{64}$
) (figure 20). Therefore, the present study utilizes generator models with the configuration of
$GM_{20}$
and with the number set of
$N_{128}$
.
Figure 21 shows variations of
$L_{2}$
,
$L_{\infty }$
,
$L_{c}$
and
$L_{mom}$
errors as a function of training iteration number for the multi-scale CNN without physical loss functions. All errors are found to converge without overfitting.
Figure 19. Configuration dependence of the generator model. (a)
$L_{2}$
, (b)
$L_{\infty }$
, (c)
$L_{c}$
and (d)
$L_{mom}$
errors from the multi-scale CNN without physical loss functions as a function of recursive prediction steps
$\unicode[STIX]{x1D6FF}t$
, where
$\unicode[STIX]{x1D6FF}t=20\unicode[STIX]{x0394}tU_{\infty }/D=0.1$
. Symbol ○ and solid line denote errors from
$GM_{16}$
; ▫ and dashed line denote errors from
$GM_{18}$
; △ and dash-dotted line denote errors from
$GM_{20}$
.
Figure 20. Number set dependence of (a)
$L_{2}$
, (b)
$L_{\infty }$
, (c)
$L_{c}$
and (d)
$L_{mom}$
errors from the multi-scale CNN without physical loss functions as a function of recursive prediction steps
$\unicode[STIX]{x1D6FF}t$
, where
$\unicode[STIX]{x1D6FF}t=20\unicode[STIX]{x0394}tU_{\infty }/D=0.1$
. Symbol ○ and solid line denote errors from
$N_{32}$
; ▫ and dashed line denote errors from
$N_{64}$
; △ and dash-dotted line denote errors from
$N_{128}$
.
Figure 21. Errors from the multi-scale CNN without physical loss functions as a function of the number of training iterations. The network is trained with flow fields at
$Re_{D}=300$
and
$500$
. The errors are evaluated for flow predictions at
$Re_{D}=400$
.
C.2 Effects of
$\unicode[STIX]{x1D706}_{adv}$
Errors
$L_{2}$
,
$L_{\infty }$
,
$L_{c}$
and
$L_{mom}$
from the GAN without physical loss functions using different adversarial training coefficients (
$\unicode[STIX]{x1D706}_{adv}=0$
, 0.05, 0.10, 0.15) are compared in figure 22. For the present parameter study,
$\unicode[STIX]{x1D706}_{l2}$
and
$\unicode[STIX]{x1D706}_{gdl}$
are fixed to 1 and
$\unicode[STIX]{x1D706}_{phy}$
is fixed to 0. The GAN is trained with flow fields at
$Re_{D}=300$
and
$500$
and tested on flow fields at
$Re_{D}=150$
,
$400$
and
$3900$
. The value of
$\unicode[STIX]{x1D706}_{adv}$
of
$0.10$
is selected for the present analysis in the results section because that case shows small
$L_{\infty }$
errors at all Reynolds numbers and the smallest
$L_{2}$
,
$L_{c}$
and
$L_{mom}$
errors at
$Re_{D}=3900$
.
C.3 Effects of
$\unicode[STIX]{x1D706}_{phy}$
Errors
$L_{2}$
,
$L_{\infty }$
,
$L_{c}$
, and
$L_{mom}$
from the multi-scale CNN with physical loss functions using different coefficients (
$\unicode[STIX]{x1D706}_{phy}=0$
, 0.10, 0.50, 1.00) are compared in figure 23. The values of
$\unicode[STIX]{x1D706}_{l2}$
and
$\unicode[STIX]{x1D706}_{gdl}$
are fixed to 1 and
$\unicode[STIX]{x1D706}_{adv}$
is fixed to 0. The multi-scale CNN is trained with flow fields at
$Re_{D}=300$
and
$500$
and tested on flow fields at
$Re_{D}=150$
,
$400$
and
$3900$
. The value of
$\unicode[STIX]{x1D706}_{phy}$
of
$1.00$
has been selected for the analysis in the results section because it shows relatively small
$L_{c}$
and
$L_{mom}$
errors at all Reynolds numbers (see figure 23).
Figure 22. Errors as a function of
$\unicode[STIX]{x1D706}_{adv}$
: ○, ▫, and
$\times$
indicate errors after
$1\unicode[STIX]{x1D6FF}t$
,
$4\unicode[STIX]{x1D6FF}t$
and
$10\unicode[STIX]{x1D6FF}t$
, respectively.
Figure 23. Errors as a function of
$\unicode[STIX]{x1D706}_{phy}$
: ○, ▫, and
$\times$
indicate errors after
$1\unicode[STIX]{x1D6FF}t$
,
$4\unicode[STIX]{x1D6FF}t$
and
$10\unicode[STIX]{x1D6FF}t$
, respectively.
Appendix D. Flow fields predicted by the GAN trained with a small time-step interval
Contour plots of the cross-stream velocity, the spanwise velocity and the pressure predicted by the GAN at
$Re_{D}=3900$
with prediction-step intervals of
$1\unicode[STIX]{x1D6FF}t$
are shown in figures 24–27.
Figure 24. Contour plots of the streamwise velocity (
$u/U_{\infty }$
) at
$Re_{D}=3900$
after
$1\unicode[STIX]{x1D6FF}t$
,
$2\unicode[STIX]{x1D6FF}t$
,
$3\unicode[STIX]{x1D6FF}t$
,
$4\unicode[STIX]{x1D6FF}t$
and
$5\unicode[STIX]{x1D6FF}t$
, where
$1\unicode[STIX]{x1D6FF}t=20\unicode[STIX]{x0394}tU_{\infty }/D=0.1$
. Flow fields at
$2\unicode[STIX]{x1D6FF}t$
,
$3\unicode[STIX]{x1D6FF}t$
,
$4\unicode[STIX]{x1D6FF}t$
and
$5\unicode[STIX]{x1D6FF}t$
are recursively predicted (utilizing flow fields predicted from prior time steps as part of the input). (a) Input set, (b) ground truth flow fields and (c) flow fields predicted by the GAN. 20 contour levels from
$-$
0.5 to 1.0 are shown. Solid lines and dashed lines indicate positive and negative contour levels, respectively.
Figure 25. Contour plots of the cross-stream velocity (
$v/U_{\infty }$
) at
$Re_{D}=3900$
after
$1\unicode[STIX]{x1D6FF}t$
,
$2\unicode[STIX]{x1D6FF}t$
,
$3\unicode[STIX]{x1D6FF}t$
,
$4\unicode[STIX]{x1D6FF}t$
and
$5\unicode[STIX]{x1D6FF}t$
, where
$1\unicode[STIX]{x1D6FF}t=20\unicode[STIX]{x0394}tU_{\infty }/D=0.1$
. Flow fields at
$2\unicode[STIX]{x1D6FF}t$
,
$3\unicode[STIX]{x1D6FF}t$
,
$4\unicode[STIX]{x1D6FF}t$
and
$5\unicode[STIX]{x1D6FF}t$
are recursively predicted (utilizing flow fields predicted from prior time steps as parts of the input). (a) Input set, (b) ground truth flow fields and (c) flow fields predicted by the GAN. 20 contour levels from
$-$
0.7 to 0.7 are shown. Solid lines and dashed lines indicate positive and negative contour levels, respectively.
Figure 26. Contour plots of the spanwise velocity (
$w/U_{\infty }$
) at
$Re_{D}=3900$
after
$1\unicode[STIX]{x1D6FF}t$
,
$2\unicode[STIX]{x1D6FF}t$
,
$3\unicode[STIX]{x1D6FF}t$
,
$4\unicode[STIX]{x1D6FF}t$
and
$5\unicode[STIX]{x1D6FF}t$
, where
$1\unicode[STIX]{x1D6FF}t=20\unicode[STIX]{x0394}tU_{\infty }/D=0.1$
. Flow fields at
$2\unicode[STIX]{x1D6FF}t$
,
$3\unicode[STIX]{x1D6FF}t$
,
$4\unicode[STIX]{x1D6FF}t$
and
$5\unicode[STIX]{x1D6FF}t$
are recursively predicted (utilizing flow fields predicted from prior time steps as part of the input). (a) Input set, (b) ground truth flow fields and (c) flow fields predicted by the GAN. 20 contour levels from
$-$
0.5 to 0.5 are shown. Solid lines and dashed lines indicate positive and negative contour levels, respectively.
Figure 27. Contour plots of the pressure (
$p/\unicode[STIX]{x1D70C}U_{\infty }^{2}$
) at
$Re_{D}=3900$
after
$1\unicode[STIX]{x1D6FF}t$
,
$2\unicode[STIX]{x1D6FF}t$
,
$3\unicode[STIX]{x1D6FF}t$
,
$4\unicode[STIX]{x1D6FF}t$
and
$5\unicode[STIX]{x1D6FF}t$
, where
$1\unicode[STIX]{x1D6FF}t=20\unicode[STIX]{x0394}tU_{\infty }/D=0.1$
. Flow fields at
$2\unicode[STIX]{x1D6FF}t$
,
$3\unicode[STIX]{x1D6FF}t$
,
$4\unicode[STIX]{x1D6FF}t$
and
$5\unicode[STIX]{x1D6FF}t$
are recursively predicted (utilizing flow fields predicted from prior time steps as part of the input). (a) Input set, (b) ground truth flow fields and (c) flow fields predicted by the GAN. 20 contour levels from
$-$
1.0 to 0.4 are shown. Solid lines and dashed lines indicate positive and negative contour levels, respectively.
Appendix E. Flow fields predicted by the GAN trained with a large time-step interval
Contour plots of the cross-stream velocity, the spanwise velocity and the pressure predicted by the GAN at
$Re_{D}=3900$
with prediction-step intervals of
$25\unicode[STIX]{x1D6FF}t$
are shown in figures 28–30 (see figure 18 for contour plots of the streamwise velocity).
Figure 28. Contour plots of the cross-stream velocity (
$v/U_{\infty }$
) at
$Re_{D}=3900$
after
$25\unicode[STIX]{x1D6FF}t$
,
$50\unicode[STIX]{x1D6FF}t$
,
$75\unicode[STIX]{x1D6FF}t$
,
$100\unicode[STIX]{x1D6FF}t$
and
$125\unicode[STIX]{x1D6FF}t$
, where
$1\unicode[STIX]{x1D6FF}t=20\unicode[STIX]{x0394}tU_{\infty }/D=0.1$
. Flow fields at
$50\unicode[STIX]{x1D6FF}t$
,
$75\unicode[STIX]{x1D6FF}t$
,
$100\unicode[STIX]{x1D6FF}t$
and
$125\unicode[STIX]{x1D6FF}t$
are recursively predicted (utilizing flow fields predicted from prior time steps as part of the input). (a) Input set, (b) ground truth flow fields and (c) flow fields predicted by the GAN. 20 contour levels from
$-$
0.7 to 0.7 are shown. Solid lines and dashed lines indicate positive and negative contour levels, respectively.
Figure 29. Contour plots of the spanwise velocity (
$w/U_{\infty }$
) at
$Re_{D}=3900$
after
$25\unicode[STIX]{x1D6FF}t$
,
$50\unicode[STIX]{x1D6FF}t$
,
$75\unicode[STIX]{x1D6FF}t$
,
$100\unicode[STIX]{x1D6FF}t$
and
$125\unicode[STIX]{x1D6FF}t$
, where
$1\unicode[STIX]{x1D6FF}t=20\unicode[STIX]{x0394}tU_{\infty }/D=0.1$
. Flow fields at
$50\unicode[STIX]{x1D6FF}t$
,
$75\unicode[STIX]{x1D6FF}t$
,
$100\unicode[STIX]{x1D6FF}t$
and
$125\unicode[STIX]{x1D6FF}t$
are recursively predicted (utilizing flow fields predicted from prior time steps as part of the input). (a) Input set, (b) ground truth flow fields and (c) flow fields predicted by the GAN. 20 contour levels from
$-$
0.5 to 0.5 are shown. Solid lines and dashed lines indicate positive and negative contour levels, respectively.
Figure 30. Contour plots of the pressure (
$p/\unicode[STIX]{x1D70C}U_{\infty }^{2}$
) at
$Re_{D}=3900$
after
$25\unicode[STIX]{x1D6FF}t$
,
$50\unicode[STIX]{x1D6FF}t$
,
$75\unicode[STIX]{x1D6FF}t$
,
$100\unicode[STIX]{x1D6FF}t$
, and
$125\unicode[STIX]{x1D6FF}t$
, where
$1\unicode[STIX]{x1D6FF}t=20\unicode[STIX]{x0394}tU_{\infty }/D=0.1$
. Flow fields at
$50\unicode[STIX]{x1D6FF}t$
,
$75\unicode[STIX]{x1D6FF}t$
,
$100\unicode[STIX]{x1D6FF}t$
and
$125\unicode[STIX]{x1D6FF}t$
are recursively predicted (utilizing flow fields predicted from prior time steps as part of the input). (a) Input set, (b) ground truth flow fields and (c) flow fields predicted by the GAN. 20 contour levels from
$-$
1.0 to 0.4 are shown. Solid lines and dashed lines indicate positive and negative contour levels, respectively.
Open access
