Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-23T12:19:37.710Z Has data issue: false hasContentIssue false
  • English
  • Français

Damping of magnetohydrodynamic waves in a rotating fluid

Published online by Cambridge University Press:  12 September 2017

Binod Sreenivasan Open the ORCID record for Binod Sreenivasan [Opens in a new window]  and
Ghanesh Narasimhan
Binod Sreenivasan*
Affiliation:
Centre for Earth Sciences, Indian Institute of Science, Bangalore 560012, India
Ghanesh Narasimhan
Affiliation:
Centre for Earth Sciences, Indian Institute of Science, Bangalore 560012, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The long-time evolution of a flow structure subject to background rotation and a coaxial uniform magnetic field is investigated in this paper. The conditions of magnetic Reynolds number 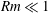$Rm\ll 1$ and Rossby number 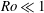$Ro\ll 1$ apply, while the condition of magnetic interaction parameter 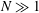$N\gg 1$ ensures that nonlinear inertial forces are small in the system. Cylindrical polar coordinates 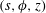$(s,\unicode[STIX]{x1D719},z)$ are used, where the velocity and the induced magnetic field are axisymmetric. Two regimes are analysed in the inviscid limit, that of strong rotation, where the inertial wave frequency is much higher than the Alfvén wave frequency, and that of weak rotation, where the Alfvén wave frequency is dominant. In either regime, the evolution consists of a damped wave-dominated phase followed by a diffusion-dominated phase. For strong rotation, the laws of energy decay in the damped wave phase are obtained by considering the decay of the fast and slow magneto-Coriolis (MC) waves individually. The diffusion-dominated phase obeys the decay laws in the well-known quasistatic approximation. The wave–diffusion transition time scale indicates that the wave phase of decay is very long, so that small-scale turbulence is characterized by damped wave motions. The ratio of kinetic to magnetic energies of the slow MC wave in the early stages of evolution is 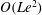$O(Le^{2})$, where 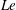$Le$ is the initial ratio of the inertial wave to Alfvén wave time scales. The induced magnetic field is hence far more efficient than the velocity in supporting slow MC waves for 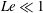$Le\ll 1$. In the regime of weak rotation, the fast and slow MC wave solutions merge and tend to the classical damped Alfvén wave solution. Here, the decay laws in non-rotating magnetohydrodynamic turbulence (Moffatt, J. Fluid Mech., vol. 28, 1967, pp. 571–592) are recovered. Computations of the general solution for the long-time decay of an isolated vortex confirm the theoretical energy scalings as well as the wave–diffusion transition time scale of the kinetic energy. It is shown that a magnetically damped system that initially generates Alfvén waves because of relatively weak rotation can subsequently give rise to MC waves. Small-scale motions of 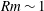$Rm\sim 1$ in the Earth’s core probably generate slow magnetostrophic waves only for 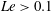$Le>0.1$, which suggests that a mean intensity of 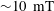${\sim}10~\text{mT}$ or higher is plausible for the toroidal magnetic field within the core.

JFM classification

Geophysical and Geological Flows: Geodynamo MHD and Electrohydrodynamics: MHD turbulence Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 828 , 10 October 2017 , pp. 867 - 905
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramovitz, M. & Stegun, I. A. 1965 Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover.Google Scholar
Acheson, D. J. & Hide, R. 1973 Hydromagnetics of rotating fluids. Rep. Prog. Phys. 36, 159–221.CrossRefGoogle Scholar
Alboussière, T., Cardin, P., Debray, F., Rizza, P. L., Masson, J.-P., Plunian, F., Ribeiro, A. & Schmitt, D. 2011 Experimental evidence of Alfvén wave propagation in a gallium alloy. Phys. Fluids 23, 096601.Google Scholar
Alemany, A., Moreau, R., Sulem, P. L. & Frisch, U. 1979 Influence of an external magnetic field on homogeneous MHD turbulence. J. Méc. 18, 277–313.Google Scholar
Bardsley, O. P. & Davidson, P. A. 2016 Inertial-Alfvén waves as columnar helices in planetary cores. J. Fluid Mech. 805, R2.Google Scholar
Braginsky, S. I. & Meytlis, V. P. 1990 Local turbulence in the Earth’s core. Geophys. Astrophys. Fluid Dyn. 55, 71–87.Google Scholar
Brito, D., Alboussiére, T., Cardin, P., Gagnière, N., Jault, D., Rizza, P. L., Masson, J.-P., Nataf, H.-C. & Schmitt, D. 2011 Zonal shear and super-rotation in a magnetized spherical Couette-flow experiment. Phys. Rev. E 83, 066310.Google Scholar
Brito, D., Cardin, P., Nataf, H.-C. & Marolleau, G. 1995 Experimental study of a geostrophic vortex of gallium in a transverse magnetic field. Phys. Earth Planet. Inter. 91, 77–98.Google Scholar
Busse, F. H. 1970 Thermal instabilities in rapidly rotating systems. J. Fluid Mech. 44, 441–460.Google Scholar
Canet, E., Finlay, C. C. & Fournier, A. 2014 Hydromagnetic quasi-geostrophic modes in rapidly rotating planetary cores. Phys. Earth Planet. Inter. 229, 1–15.Google Scholar
Galtier, S. 2014 Weak turbulence theory for rotating magnetohydrodynamics and planetary flows. J. Fluid Mech. 757, 114–154.Google Scholar
Gillet, N., Jault, D., Canet, E. & Fournier, A. 2010 Fast torsional waves and strong magnetic field within the Earth’s core. Nature 465, 74–77.Google Scholar
Gillet, N., Schaeffer, N. & Jault, D. 2011 Rationale and geophysical evidence for quasi-geostrophic rapid dynamics within the Earth’s outer core. Phys. Earth Planet. Inter. 187, 380–390.Google Scholar
Gopinath, V. & Sreenivasan, B. 2015 On the control of rapidly rotating convection by an axially varying magnetic field. Geophys. Astrophys. Fluid Dyn. 109, 567–586.Google Scholar
Gradshteyn, I. S. & Ryzhik, I. M. 2007 Table of Integrals, Series and Products. Academic.Google Scholar
Hori, K., Jones, C. A. & Teed, R. J. 2015 Slow magnetic Rossby waves in the Earth’s core. Geophys. Res. Lett. 42, 6622–6629.Google Scholar
Jameson, A.1961 Magnetohydrodynamic waves. PhD dissertation, University of Cambridge.Google Scholar
Jault, D. 2008 Axial invariance of rapidly varying diffusionless motions in the Earth’s core interior. Phys. Earth Planet. Inter. 166, 67–76.Google Scholar
Kono, M. & Roberts, P. H. 2002 Recent geodynamo simulations and observations of the geomagnetic field. Rev. Geophys. 40 (4), 1013.Google Scholar
Lehnert, B. 1954 Magnetohydrodynamic waves under the action of the Coriolis force. Astrophys. J. 119, 647–654.Google Scholar
Lehnert, B. 1955 The decay of magneto-turbulence in the presence of a magnetic field and Coriolis force. Q. Appl. Maths 12, 321–341.Google Scholar
Moffatt, H. K. 1967 On the suppression of turbulence by a uniform magnetic field. J. Fluid Mech. 28, 571–592.Google Scholar
Moffatt, H. K. & Loper, D. E. 1994 The magnetostrophic rise of a buoyant parcel in the Earth’s core. Geophys. J. Intl 117, 394–402.Google Scholar
Nataf, H.-C. & Schaeffer, N. 2015 Turbulence in the core. In Core Dynamics (ed. Olson, P.), Treatise on Geophysics, vol. 8, pp. 161–181. Elsevier.Google Scholar
Olson, P. 2015 Core dynamics: an introduction and overview. In Core Dynamics (ed. Olson, P.), Treatise on Geophysics, vol. 8, pp. 1–25. Elsevier.Google Scholar
Roberts, P. H. 1967 An Introduction to Magnetohydrodynamics. Longmans.Google Scholar
Schmitt, D. 2012 Quasi-free-decay magnetic modes in planetary cores. Geophys. Astrophys. Fluid Dyn. 106, 660–680.Google Scholar
Siso-Nadal, F. & Davidson, P. A. 2004 Anisotropic evolution of small isolated vortices within the core of the Earth. Phys. Fluids 16, 1242–1254.Google Scholar
Siso-Nadal, F., Davidson, P. A. & Graham, W. R. 2003 Evolution of a vortex in a rotating conducting fluid. J. Fluid Mech. 493, 181–190.Google Scholar
Soderlund, K. M., King, E. M. & Aurnou, J. M. 2012 The influence of magnetic fields in planetary dynamo models. Earth Planet. Sci. Lett. 333–334, 9–20.Google Scholar
Sreenivasan, B. 2010 Modelling the geodynamo: progress and challenges. Curr. Sci. 99 (12), 1739–1750.Google Scholar
Sreenivasan, B. & Alboussière, T. 2002 Experimental study of a vortex in a magnetic field. J. Fluid Mech. 464, 287–309.Google Scholar
Sreenivasan, B. & Gopinath, V. 2017 Confinement of rotating convection by a laterally varying magnetic field. J. Fluid Mech. 822, 590–616.Google Scholar
Sreenivasan, B. & Jones, C. A. 2011 Helicity generation and subcritical behaviour in rapidly rotating dynamos. J. Fluid Mech. 688, 5–30.Google Scholar
St. Pierre, M. G. 1996 On the local nature of turbulence in Earth’s outer core. Geophys. Astrophys. Fluid Dyn. 83, 293–306.Google Scholar
Starchenko, S. & Jones, C. A. 2002 Typical velocities and magnetic fields in planetary interiors. Icarus 157, 426–435.Google Scholar
Steenbeck, M., Krause, F. & Rädler, K. H. 1966 A calculation of the mean electromotive force in an electrically conducting fluid in turbulent motion, under the influence of Coriolis forces. Z. Naturforsch. 21a, 369–376.Google Scholar
Stieglitz, R. & Müller, U. 2001 Experimental demonstration of a homogeneous two-scale dynamo. Phys. Fluids 13, 561–564.Google Scholar
Teed, R., Jones, C. A. & Tobias, S. M. 2015 The transition to Earth-like torsional oscillations in magnetoconvection simulations. Earth Planet. Sci. Lett. 419, 22–31.Google Scholar
Weisstein, E. W. 2003 CRC Concise Encyclopedia of Mathematics. Chapman and Hall/CRC.Google Scholar