A new damping mechanism for vertically-sheared inertial motions is described involving an inertia–gravity wave that oscillates at half the inertial frequency, 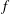$f$, and that grows at the expense of inertial shear. This parametric subharmonic instability forms in baroclinic, geostrophic currents where thermal wind shear, by reducing the potential vorticity of the fluid, allows inertia–gravity waves with frequencies less than 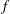$f$. A stability analysis and numerical simulations are used to study the instability criterion, energetics, and finite-amplitude behaviour of the instability. For a flow with uniform shear and stratification, parametric subharmonic instability develops when the Richardson number of the geostrophic current nears 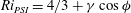$Ri_{PSI}=4/3+\gamma \cos \phi $, where 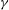$\gamma $ is the ratio of the inertial to thermal wind shear magnitude and 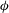$\phi $ is the angle between the inertial and thermal wind shears at the initial time. Inertial shear enters the instability criterion because it can also modify the potential vorticity and hence the minimum frequency of inertia–gravity waves. When this criterion is met, inertia–gravity waves with a frequency 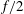$f/2$ and with flow parallel to isopycnals amplify, extracting kinetic energy from the inertial shear through shear production. The solutions of the numerical simulations are consistent with these predictions and additionally show that finite-amplitude parametric subharmonic instability both damps inertial shear and is itself damped by secondary shear instabilities. In this way, parametric subharmonic instability opens a pathway to turbulence where kinetic energy in inertial shear is transferred to small scales and dissipated.