Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
García-Soriano, Gabriel
Castillo, José Luis
Higuera, Francisco J.
and
García-Ybarra, Pedro L.
2012.
Local burning velocity in a Bunsen jet flame
.
Comptes Rendus. Mécanique,
Vol. 340,
Issue. 11-12,
p.
789.
Assier, Raphaël C.
and
Wu, Xuesong
2014.
Linear and weakly nonlinear instability of a premixed curved flame under the influence of its spontaneous acoustic field.
Journal of Fluid Mechanics,
Vol. 758,
Issue. ,
p.
180.
Sánchez, Antonio L.
and
Williams, Forman A.
2014.
Recent advances in understanding of flammability characteristics of hydrogen.
Progress in Energy and Combustion Science,
Vol. 41,
Issue. ,
p.
1.
Wu, Fujia
Saha, Abhishek
Chaudhuri, Swetaprovo
and
Law, Chung K.
2014.
Facilitated Ignition in Turbulence through Differential Diffusion.
Physical Review Letters,
Vol. 113,
Issue. 2,
Chaudhuri, Swetaprovo
Saha, Abhishek
and
Law, Chung K.
2015.
On flame–turbulence interaction in constant-pressure expanding flames.
Proceedings of the Combustion Institute,
Vol. 35,
Issue. 2,
p.
1331.
Lu, Xiaoyi
and
Pantano, Carlos
2015.
Linear stability analysis of a premixed flame with transverse shear.
Journal of Fluid Mechanics,
Vol. 765,
Issue. ,
p.
150.
Uranakara, Harshavardhana A.
Chaudhuri, Swetaprovo
Dave, Himanshu L.
Arias, Paul G.
and
Im, Hong G.
2016.
A flame particle tracking analysis of turbulence–chemistry interaction in hydrogen–air premixed flames
.
Combustion and Flame,
Vol. 163,
Issue. ,
p.
220.
Kazakov, Kirill A.
2016.
Premixed flame propagation in vertical tubes.
Physics of Fluids,
Vol. 28,
Issue. 4,
Thiesset, F.
Halter, F.
Bariki, C.
Lapeyre, C.
Chauveau, C.
Gökalp, I.
Selle, L.
and
Poinsot, T.
2017.
Isolating strain and curvature effects in premixed flame/vortex interactions.
Journal of Fluid Mechanics,
Vol. 831,
Issue. ,
p.
618.
Kazakov, Kirill A.
and
Kharlanov, Oleg G.
2018.
Numerical study of strongly-nonlinear regimes of steady premixed flame propagation. The effect of thermal gas expansion and finite-front-thickness effects.
Combustion Theory and Modelling,
Vol. 22,
Issue. 5,
p.
835.
Yoon, Sung Hwan
Hu, Longhua
and
Fujita, Osamu
2018.
Experimental observation of pulsating instability under acoustic field in downward-propagating flames at large Lewis number.
Combustion and Flame,
Vol. 188,
Issue. ,
p.
1.
Al Sarraf, Elias
Almarcha, Christophe
Quinard, Joël
Radisson, Basile
Denet, Bruno
and
Garcia-Ybarra, Pedro
2019.
Darrieus–Landau instability and Markstein numbers of premixed flames in a Hele-Shaw cell.
Proceedings of the Combustion Institute,
Vol. 37,
Issue. 2,
p.
1783.
Garcia-Soriano, Gabriel
Margenat, Sergio
Higuera, Francisco J.
Castillo, Jose L.
and
Garcia-Ybarra, Pedro L.
2019.
Non-linear response of the flame velocity to moderately large curvatures in laminar jet flames of methane–air mixtures.
Combustion and Flame,
Vol. 205,
Issue. ,
p.
123.
Rajamanickam, Prabakaran
Coenen, Wilfried
Sánchez, Antonio L.
and
Williams, Forman A.
2019.
Influences of stoichiometry on steadily propagating triple flames in counterflows.
Proceedings of the Combustion Institute,
Vol. 37,
Issue. 2,
p.
1971.
Garcia-Soriano, G.
Margenat, S.
Higuera, F.J.
Castillo, J.L.
and
Garcia-Ybarra, P.L.
2020.
Experimental limit on the validity of Markstein relation.
Experimental Thermal and Fluid Science,
Vol. 116,
Issue. ,
p.
110129.
Di Sabatino, Francesco
Guiberti, Thibault F.
Moeck, Jonas P.
Roberts, William L.
and
Lacoste, Deanna A.
2020.
Fuel and Equivalence Ratio Effects on Transfer Functions of Premixed Swirl Flames.
Journal of Propulsion and Power,
Vol. 36,
Issue. 2,
p.
271.
Berger, Lukas
Hesse, Raik
Kleinheinz, Konstantin
Hegetschweiler, Michael J.
Attili, Antonio
Beeckmann, Joachim
Linteris, Gregory T.
and
Pitsch, Heinz
2020.
A DNS study of the impact of gravity on spherically expanding laminar premixed flames.
Combustion and Flame,
Vol. 216,
Issue. ,
p.
412.
Wang, Yiqing
Jayachandran, Jagannath
and
Chen, Zheng
2020.
Effects of pressure rise rate on laminar flame speed under normal and engine-relevant conditions.
Combustion Theory and Modelling,
Vol. 24,
Issue. 5,
p.
953.
Dave, Himanshu L.
and
Chaudhuri, Swetaprovo
2020.
Evolution of local flame displacement speeds in turbulence.
Journal of Fluid Mechanics,
Vol. 884,
Issue. ,
Howarth, T.L.
and
Aspden, A.J.
2022.
An empirical characteristic scaling model for freely-propagating lean premixed hydrogen flames.
Combustion and Flame,
Vol. 237,
Issue. ,
p.
111805.
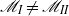 characterize usual wrinkled flames sustained by a multiple-step chemical network,
characterize usual wrinkled flames sustained by a multiple-step chemical network, 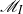 for the modification of the flame velocity due to the curvature of the front and
for the modification of the flame velocity due to the curvature of the front and 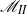 for the effect of the flow strain rate. In contrast to
for the effect of the flow strain rate. In contrast to 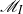 ,
, 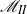 depends on the location of the flame surface within the flame thickness, in such a way that the final result for the flame dynamics is not depending on this choice. The first part of the paper is devoted to present a general method of solution, valid for any multiple-step chemical network. The two Markstein numbers for two-step chain-branching models representing rich hydrogen–air flames and lean hydrocarbon–air flames are then computed analytically in the second part.
depends on the location of the flame surface within the flame thickness, in such a way that the final result for the flame dynamics is not depending on this choice. The first part of the paper is devoted to present a general method of solution, valid for any multiple-step chemical network. The two Markstein numbers for two-step chain-branching models representing rich hydrogen–air flames and lean hydrocarbon–air flames are then computed analytically in the second part.