Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T06:43:49.318Z Has data issue: false hasContentIssue false
  • English
  • Français

Curvature instability of a curved Batchelor vortex

Published online by Cambridge University Press:  06 February 2017

Francisco J. Blanco-Rodríguez  and
Stéphane Le Dizès Open the ORCID record for Stéphane Le Dizès [Opens in a new window]
Francisco J. Blanco-Rodríguez
Affiliation:
Aix Marseille Univ., CNRS, Centrale Marseille, IRPHE, 13384 Marseille, France
Stéphane Le Dizès*
Affiliation:
Aix Marseille Univ., CNRS, Centrale Marseille, IRPHE, 13384 Marseille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we analyse the curvature instability of a curved Batchelor vortex. We consider this short-wavelength instability when the radius of curvature of the vortex centreline is large compared with the vortex core size. In this limit, the curvature instability can be interpreted as a resonant phenomenon. It results from the resonant coupling of two Kelvin modes of the underlying Batchelor vortex with the dipolar correction induced by curvature. The condition of resonance of the two modes is analysed in detail as a function of the axial jet strength of the Batchelor vortex. 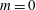In contrast to the Rankine vortex, only a few configurations involving $m=0$ and 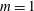$m=1$ modes are found to become the most unstable. The growth rate of the resonant configurations is systematically computed and used to determine the characteristics of the most unstable mode as a function of the curvature ratio, the Reynolds number and the axial flow parameter. The competition of the curvature instability with another short-wavelength instability, which was considered in a companion paper (Blanco-Rodríguez & Le Dizès, J. Fluid Mech., vol. 804, 2016, pp. 224–247), is analysed for a vortex ring. A numerical error found in this paper, which affects the relative strength of the elliptic instability, is also corrected. We show that the curvature instability becomes the dominant instability in large rings as soon as axial flow is present (vortex ring with swirl).

JFM classification

Vortex Flows: Vortex Flows Vortex Flows: Vortex instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 814 , 10 March 2017 , pp. 397 - 415
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bayly, B. J. 1986 Three-dimensional instability of elliptical flow. Phys. Rev. Lett. 57, 2160–2163.CrossRefGoogle ScholarPubMed
Blanco-Rodríguez, F. J. & Le Dizès, S. 2016 Elliptic instability of a curved Batchelor vortex. J. Fluid Mech. 804, 224–247.Google Scholar
Blanco-Rodríguez, F. J., Le Dizès, S., Selçuk, C., Delbende, I. & Rossi, M. 2015 Internal structure of vortex rings and helical vortices. J. Fluid Mech. 785, 219–247.Google Scholar
Callegari, A. J. & Ting, L. 1978 Motion of a curved vortex filament with decaying vortical core and axial velocity. SIAM J. Appl. Maths 35, 148–175.Google Scholar
Crow, S. C. 1970 Stability theory for a pair of trailing vortices. AIAA J. 8 (12), 2172–2179.CrossRefGoogle Scholar
Eloy, C. & Le Dizès, S. 1999 Three-dimensional instability of Burgers and Lamb–Oseen vortices in a strain field. J. Fluid Mech. 378, 145–166.CrossRefGoogle Scholar
Eloy, C. & Le Dizès, S. 2001 Stability of the Rankine vortex in a multipolar strain field. Phys. Fluids 13 (3), 660–676.Google Scholar
Fabre, D. & Jacquin, L. 2004a Short-wave cooperative instabilities in representative aircraft vortices. Phys. Fluids 16, 1366–1378.Google Scholar
Fabre, D. & Jacquin, L. 2004b Viscous instabilities in trailing vortices at large swirl numbers. J. Fluid Mech. 500, 239–262.CrossRefGoogle Scholar
Fabre, D., Sipp, D. & Jacquin, L. 2006 The Kelvin waves and the singular modes of the Lamb–Oseen vortex. J. Fluid Mech. 551, 235–274.Google Scholar
Feys, J. & Maslowe, S. A. 2016 Elliptical instability of the Moore–Saffman model for a trailing wingtip vortex. J. Fluid Mech. 803, 556–590.Google Scholar
Fukumoto, Y. 2003 The three-dimensional instability of a strained vortex tube revisited. J. Fluid Mech. 493, 287–318.Google Scholar
Fukumoto, Y. & Hattori, Y. 2005 Curvature instability of a vortex ring. J. Fluid Mech. 526, 77–115.Google Scholar
Hattori, Y. & Fukumoto, Y. 2003 Short-wavelength stability analysis of thin vortex rings. Phys. Fluids 15, 3151–3163.Google Scholar
Hattori, Y. & Fukumoto, Y. 2009 Short-wavelength stability analysis of a helical vortex tube. Phys. Fluids 21, 014104.Google Scholar
Hattori, Y. & Fukumoto, Y. 2010 Short-wave stability of a helical vortex tube: the effect of torsion on the curvature instability. Theor. Comput. Fluid Dyn. 24, 363–368.Google Scholar
Hattori, Y. & Fukumoto, Y. 2012 Effects of axial flow on the stability of a helical vortex tube. Phys. Fluids 24, 054102.CrossRefGoogle Scholar
Hattori, Y. & Fukumoto, Y. 2014 Modal stability analysis of a helical vortex tube with axial flow. J. Fluid Mech. 738, 222–249.Google Scholar
Lacaze, L., Ryan, K. & Le Dizès, S. 2007 Elliptic instability in a strained Batchelor vortex. J. Fluid Mech. 577, 341–361.CrossRefGoogle Scholar
Le Dizès, S. 2004 Viscous critical-layer analysis of vortex normal modes. Stud. Appl. Maths 112 (4), 315–332.Google Scholar
Le Dizès, S. 2008 Inviscid waves on a Lamb–Oseen vortex in a rotating stratified fluid: consequences on the elliptic instability. J. Fluid Mech. 597, 283–303.Google Scholar
Le Dizès, S. & Fabre, D. 2007 Large-Reynolds-number asymptotic analysis of viscous centre modes in vortices. J. Fluid Mech. 585, 153–180.CrossRefGoogle Scholar
Le Dizès, S. & Lacaze, L. 2005 An asymptotic description of vortex Kelvin modes. J. Fluid Mech. 542, 69–96.Google Scholar
Le Dizès, S. & Laporte, F. 2002 Theoretical predictions for the elliptic instability in a two-vortex flow. J. Fluid Mech. 471, 169–201.Google Scholar
Lifschitz, A. & Hameiri, E. 1991 Local stability conditions in fluid dynamics. Phys. Fluids A 3 (11), 2644–2651.Google Scholar
Mayer, E. W. & Powell, K. G. 1992 Viscous and inviscid instabilities of a trailing vortex. J. Fluid Mech. 245, 91–114.Google Scholar
Moore, D. W. & Saffman, P. G. 1973 Axial flow in laminar trailing vortices. Proc. R. Soc. Lond. A 333, 491–508.Google Scholar
Moore, D. W. & Saffman, P. G. 1975 The instability of a straight vortex filament in a strain field. Proc. R. Soc. Lond. A 346, 413–425.Google Scholar
Quaranta, H. U., Bolnot, H. & Leweke, T. 2015 Long-wave instability of a helical vortex. J. Fluid Mech. 780, 687–716.Google Scholar
Shariff, K. & Leonard, A. 1992 Vortex rings. Annu. Rev. Fluid Mech. 24, 235–279.Google Scholar
Sipp, D. & Jacquin, L. 2003 Widnall instabilities in vortex pairs. Phys. Fluids 15, 1861–1874.Google Scholar
Spalart, P. R. 1998 Airplane trailing vortices. Annu. Rev. Fluid Mech. 30, 107–138.Google Scholar
Tsai, C.-Y. & Widnall, S. E. 1976 The stability of short waves on a straight vortex filament in a weak externally imposed strain field. J. Fluid Mech. 73 (4), 721–733.CrossRefGoogle Scholar
Waleffe, F. 1990 On the three-dimensional instability of strained vortices. Phys. Fluids A 2 (1), 76–80.Google Scholar
Widnall, S. E. 1972 The stability of a helical vortex filament. J. Fluid Mech. 54, 641–663.Google Scholar
Widnall, S. E., Bliss, D. & Tsai, C.-Y. 1974 The instability of short waves on a vortex ring. J. Fluid Mech. 66 (1), 35–47.Google Scholar
Widnall, S. E. & Tsai, C.-Y. 1977 The instability of the thin vortex ring of constant vorticity. Phil. Trans. R. Soc. Lond. 287, 273–305.Google Scholar
Supplementary material: File

Blanco-Rodríguez and Le Dizès supplementary material

Blanco-Rodríguez and Le Dizès supplementary material 1

Download Blanco-Rodríguez and Le Dizès supplementary material(File)
File 141.3 KB