Article contents
Cross-stream migration of non-spherical particles in a second-order fluid – theories of particle dynamics in arbitrary quadratic flows
Published online by Cambridge University Press: 15 May 2020
Abstract
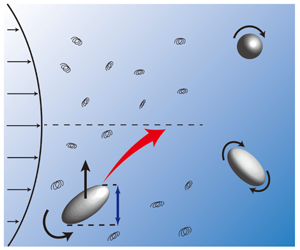
Particle migration in viscoelastic suspensions is vital in many applications in the biomedical community and the chemical/oil industries. Previous studies have provided insight into the motion of spherical particles in simple viscoelastic flows, yet the combined effect of more complex flow profiles and particle shapes is under-explored. Here, we develop approximate analytical expressions for the polymeric force and torque on an arbitrarily shaped particle in a second-order fluid, subject to a general quadratic flow field. This model is exact for the case when the first and second normal stress coefficients satisfy  $\unicode[STIX]{x1D713}_{1}=-2\unicode[STIX]{x1D713}_{2}$. Under this assumption, we examine how particle shape alters cross-stream particle migration (i.e. lift) and particle orientation in both shear- and pressure-driven flows. In shear-driven flows, we observe that spheroidal particles adjust their orientation to align their longer axis along the vorticity direction, although significant deviations from slender-body theories occur for finite aspect ratios. In a slit-like pressure-driven flow, we identify scaling theories to quantify how the particle lift depends on shape for a wide variety of shapes. We find that prolate particles slowly transition to a log-rolling state as they approach the flow centre, with the lift initially being larger than that of an equal-volume sphere, but then becoming smaller as log-rolling emerges. The net effect is a smaller average migration speed for particles with larger aspect ratio. Lastly, we discuss future directions for experimental studies on particle dynamics as well as directions to extend the current work towards more complicated systems.
$\unicode[STIX]{x1D713}_{1}=-2\unicode[STIX]{x1D713}_{2}$. Under this assumption, we examine how particle shape alters cross-stream particle migration (i.e. lift) and particle orientation in both shear- and pressure-driven flows. In shear-driven flows, we observe that spheroidal particles adjust their orientation to align their longer axis along the vorticity direction, although significant deviations from slender-body theories occur for finite aspect ratios. In a slit-like pressure-driven flow, we identify scaling theories to quantify how the particle lift depends on shape for a wide variety of shapes. We find that prolate particles slowly transition to a log-rolling state as they approach the flow centre, with the lift initially being larger than that of an equal-volume sphere, but then becoming smaller as log-rolling emerges. The net effect is a smaller average migration speed for particles with larger aspect ratio. Lastly, we discuss future directions for experimental studies on particle dynamics as well as directions to extend the current work towards more complicated systems.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 14
- Cited by


