Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-26T22:28:18.279Z Has data issue: false hasContentIssue false
  • English
  • Français

Critical selection of shear sheltering in electroconvective flow from chaotic to steady state

Published online by Cambridge University Press:  01 August 2022

Wei Liu Open the ORCID record for Wei Liu [Opens in a new window] ,
Yueting Zhou Open the ORCID record for Yueting Zhou [Opens in a new window]  and
Pengpeng Shi Open the ORCID record for Pengpeng Shi [Opens in a new window]
Wei Liu
Affiliation:
School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, PR China Shanghai Key Lab of Vehicle Aerodynamics and Vehicle Thermal Management Systems, Shanghai 201804, PR China
Yueting Zhou*
Affiliation:
School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, PR China Shanghai Key Lab of Vehicle Aerodynamics and Vehicle Thermal Management Systems, Shanghai 201804, PR China
Pengpeng Shi*
Affiliation:
School of Civil Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, Shaanxi, PR China State Key Laboratory for Strength and Vibration of Mechanical Structures, Shaanxi Engineering Research Centre of NDT and Structural Integrity Evaluation, School of Aerospace, Xi'an Jiaotong University, Xi'an 710049, Shaanxi, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

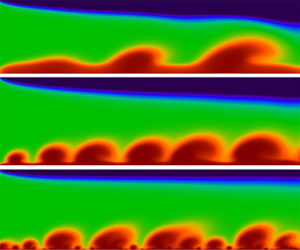
Ion and water are transported by electroconvection near permselective membranes, resulting in complex phenomena associated with the flow–fines interaction. Sheltering the flow chaos by the shear flow is a common strategy in plasma fluids and has recently been successfully applied to control ionic fluids. The paper herein reveals the critical selection of shear velocity regarding the fluid from a chaotic to a steady state through numerical and theoretical analyses. For the shear sheltering, the dimensionless Debye length ${\lambda _D}$ with varying channel height is introduced to achieve a comprehensive discussion of the factors and laws affecting the shear vortex state. Based on an analysis of the vortex driving mechanism, the scaling of the slip velocity ${u_s}\sim {(\lambda _D^{ - 1}\Delta {\phi ^4})^{1/3}}$ is recommended as the critical selection factor for the steady and chaotic state under a fixed shear flow velocity, which involves the dimensionless Debye length ${\lambda _D}$ and voltage difference $\Delta \phi $. Furthermore, for ionic fluid control by shear flow, a critical shear velocity ${U_{HPC}}$ is proposed to distinguish the electroconvective flow from a chaotic state to a steady state. When the shear flow velocity ${U_{HP}} > {U_{HPC}}$, the shear flow shelters chaos, and the scaling law is also recommended for the regulation of the critical shear flow velocity ${U_{HPC}}$ jointly by ${\lambda _D}$ and $\Delta \phi $. The analysis is confirmed by direct numerical simulation and existing experimental data (J. Fluid Mech, vol. 813, 2017, pp. 799–823). This work provides a more comprehensive physical insight for shear sheltering and affects the design of electromembrane microfluidics.

JFM classification

MHD and Electrohydrodynamics: Electrokinetic flows Micro-/Nano-fluid dynamics: Microscale transport Flow Control: Instability control
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 946 , 10 September 2022 , A3
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aboelkassem, Y. 2019 Pumping flow model in a microchannel with propagative rhythmic membrane contraction. Phys. Fluids 31 (5), 51902.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, A.D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection. Rev. Mod. Phys. 81 (2), 503.CrossRefGoogle Scholar
Chen, Q., Zhu, H., Yan, Z., Ju, J.W., Jiang, Z. & Wang, Y. 2016 A multiphase micromechanical model for hybrid fiber reinforced concrete considering the aggregate and ITZ effects. Const. Build. Mater. 114, 839–850.CrossRefGoogle Scholar
Chuang, J.N., Diao, P.Y., Huang, W.S., Huang, L.F., Senapati, S., Chang, H.C. & Sun, Y.M. 2020 Novel homogeneous anion exchange membranes for reproducible and sensitive nucleic acid detection via current–voltage characteristic measurement. ACS Appl. Mater. Interfaces 12 (49), 54459–54472.CrossRefGoogle ScholarPubMed
Davidson, S.M., Andersen, M.B. & Mani, A. 2014 Chaotic induced-charge electro-osmosis. Phys. Rev. Lett. 112 (12), 128302.CrossRefGoogle ScholarPubMed
De Valenca, J.C., Kurniawan, A., Wagterveld, M.R., Wood, J.A. & Lammertink, R.G.H. 2017 Influence of Rayleigh-Bénard convection on electrokinetic instability in overlimiting current conditions. Phys. Rev. Fluids 2 (3), 033701.CrossRefGoogle Scholar
Demekhin, E.A., Amiroudine, S.G., Ganchenko, S. & Khasmatulina, N.Y. 2015 Thermoelectro- convection near charge-selective surfaces. Phys. Rev. E 91 (6), 063006.CrossRefGoogle Scholar
Demekhin, E.A., Nikitin, N.V. & Shelistov, V.S. 2013 Direct numerical simulation of electrokinetic instability and transition to chaotic motion. Phys. Fluids 25 (12), 122001.CrossRefGoogle Scholar
Demekhin, E.A., Shelistov, V.S. & Polyanskikh, S.V. 2011 Linear and nonlinear evolution and diffusion layer selection in electrokinetic instability. Phys. Rev. E 84 (3), 036318.CrossRefGoogle ScholarPubMed
Druzgalski, C.L., Andersen, M.B. & Mani, A. 2013 Direct numerical simulation of electroconvective instability and hydrodynamic chaos near an ion-selective surface. Phys. Fluids 25 (11), 110804.CrossRefGoogle Scholar
Druzgalski, C.L. & Mani, A. 2016 Statistical analysis of electroconvection near an ion-selective membrane in the highly chaotic regime. Phys. Rev. Fluids 1 (7), 073601.CrossRefGoogle Scholar
Green, Y. 2020 Approximate time-dependent current-voltage relations for currents exceeding the diffusion limit. Phys. Rev. E 101 (4), 043113.CrossRefGoogle ScholarPubMed
Guan, Y. & Novosselov, I. 2019 Two relaxation time lattice Boltzmann method coupled to fast Fourier transform Poisson solver: application to electroconvective flow. J. Comput. Phys. 397, 108830.CrossRefGoogle ScholarPubMed
Guan, Y.F., Riley, J. & Novosselov, I. 2020 Three-dimensional electroconvective vortices in cross flow. Phys. Rev. E 101 (03), 033103.CrossRefGoogle ScholarPubMed
Guan, Y., Yang, T. & Wu, J. 2021 Mixing and transport enhancement in microchannels by electrokinetic flows with charged surface heterogeneity. Phys. Fluids 33 (4), 042006.CrossRefGoogle Scholar
Hasan, M.K. & Gross, A. 2020 Temporal secondary stability simulation of Rayleigh–Benard– Poiseuille flow. Intl J. Heat Mass Transfer 159, 120098.CrossRefGoogle Scholar
Hasan, M.K. & Gross, A. 2021 Numerical instability investigation of inward radial Rayleigh–Benard– Poiseuille flow. Phys. Fluids 33 (3), 034120.CrossRefGoogle Scholar
Huisman, S.G., Scharnowski, S., Cierpka, C., Kahler, C.J., Lohse, A.D. & Sun, C. 2013 Logarithmic boundary layers in strong Taylor-Couette turbulence. Phys. Rev. Lett. 110 (26), 264501.CrossRefGoogle ScholarPubMed
Kang, S. & Kwak, R. 2020 Pattern formation of three-dimensional electroconvection on a charge selective surface. Phys. Rev. Lett. 124 (15), 154502.CrossRefGoogle ScholarPubMed
Karatay, E., Andersen, M.B., Wessling, M. & Mani, A. 2016 Coupling between buoyancy forces and electroconvective instability near ion-selective surfaces. Phys. Rev. Lett. 116 (19), 194501.CrossRefGoogle ScholarPubMed
Kim, S.J., Ko, S.H., Kang, K.H. & Han, J. 2010 Direct seawater desalination by ion concentration polarization. Nat. Nanotechnol. 5 (4), 297–301.CrossRefGoogle ScholarPubMed
Kühnen, J., Song, B., Scarselli, D., Budanur, N.B., Riedl, M., Willis, A.P., Avila, M. & Hof, B. 2018 Destabilizing turbulence in pipe flow. Nat. Phys. 14 (14), 386–390.CrossRefGoogle Scholar
Kwak, R., Guan, G., Peng, W.K. & Han, J. 2013 a Microscale electrodialysis: concentration profiling and vortex visualization. Desalination 308, 138–146.CrossRefGoogle Scholar
Kwak, R., Pham, V.S. & Han, J. 2017 Sheltering the perturbed vortical layer of electroconvection under shear flow. J. Fluid Mech. 813, 799–823.CrossRefGoogle Scholar
Kwak, R., Pham, V.S., Lim, K.M. & Han, J. 2013 b Shear flow of an electrically charged fluid by ion concentration polarization: scaling laws for electroconvective vortices. Phys. Rev. Lett. 110 (11), 114501.CrossRefGoogle ScholarPubMed
Li, G., Archer, L.A. & Koch, D.L. 2019 Electroconvection in a viscoelastic electrolyte. Phys. Rev. Lett. 122 (12), 12450.CrossRefGoogle Scholar
Liu, W., Zhou, Y. & Shi, P. 2020 a Electrokinetic ion transport at micro–nanochannel interfaces: applications for desalination and micromixing. Appl. Nanosci. 10 (3), 751–776.CrossRefGoogle Scholar
Liu, W., Zhou, Y. & Shi, P. 2020 b Scaling laws of electroconvective flow with finite vortex height near permselective membranes. Phys. Rev. E 102 (3), 033102.CrossRefGoogle ScholarPubMed
Liu, W., Zhou, Y. & Shi, P. 2020 c shear electroconvective instability in electrodialysis channel under extreme depletion and its scaling laws. Phys. Rev. E 101 (4), 043105.CrossRefGoogle ScholarPubMed
Luo, K., Wu, J., Yi, H.L. & Tan, H.P. 2020 Numerical analysis of two-phase electrohydrodynamic flows in the presence of surface charge convection. Phys. Fluids 32 (12), 123606.CrossRefGoogle Scholar
Mani, A. & Wang, K.M. 2020 Electroconvection near electrochemical interfaces: experiments, modeling, and computation. Annu. Rev. Fluid Mech. 52, 509–529.CrossRefGoogle Scholar
Nakayama, A., Sano, Y., Bai, X. & Tado, K. 2017 A boundary layer analysis for determination of the limiting current density in an electrodialysis desalination. Desalination 404, 41–49.CrossRefGoogle Scholar
Nikonenko, V.V., Vasil'eva, V.I., Akberova, E.M., Uzdenova, A.M., Urtenovb, M.K., Kovalenko, A.V., Pismenskaya, N.P., Mareev, S.A. & Pourcelly, G. 2016 Competition between diffusion and electroconvection at an ion-selective surface in intensive current regimes. Adv. Colloid Interface Sci. 235, 233–246.CrossRefGoogle ScholarPubMed
Ouyang, W., Ye, X.H., Li, Z.R. & Han, J. 2018 Deciphering ion concentration polarization-based electrokinetic molecular concentration at the micro-nanofluidic interface: theoretical limits and scaling laws. Nanoscale 10 (32), 15187–15194.CrossRefGoogle ScholarPubMed
Peng, R. & Li, D. 2015 Effects of ionic concentration gradient on electroosmotic flow mixing in a microchannel. J. Colloid Interface Sci. 440, 126–132.CrossRefGoogle Scholar
Pham, V.S., Li, Z.R., Lim, K.M., White, J.K. & Han, J. 2012 Direct numerical simulation of electroconvective instability and hysteretic current-voltage response of a permselective membrane. Phys. Rev. E 86 (4), 046310.CrossRefGoogle ScholarPubMed
Qiu, B.L., Gong, L.Y., Li, Z.R. & Han, J. 2019 Electrokinetic flow in the U-shaped micro-nanochannels. Theor. Appl. Mech. Lett. 9 (1), 36–42.CrossRefGoogle Scholar
Rubinstein, S.M., Manukyan, G., Staicu, A., Rubinstein, I., Zaltzman, B., Lammertink, R.G.H., Mugele, F. & Wessling, M. 2008 Direct observation of a nonequilibrium electro-osmotic instability. Phys. Rev. Lett. 101, 236101.CrossRefGoogle ScholarPubMed
Rubinstein, I. & Shtilman, L. 1979 Voltage against current curves of cation exchange membranes. J. Chem. Soc. Faraday Trans. 75, 231–246.CrossRefGoogle Scholar
Rubinstein, I. & Zaltzman, B. 2000 Electro-osmotically induced convection at a permselective membrane. Phys. Rev. E 62, 2238–2251.CrossRefGoogle Scholar
Rubinstein, I. & Zaltzman, B. 2001 Electro-osmotic slip of the second kind and instability in concentration polarization at electrodialysis membranes. Math. Models Meth. Appl. Sci. 11 (2), 263–300.CrossRefGoogle Scholar
Rubinstein, I. & Zaltzman, B. 2015 Equilibrium electroconvective instability. Phys. Rev. Lett. 114, 114502.CrossRefGoogle ScholarPubMed
Shelistov, V.S., Demekhin, E.A. & Ganchenko, G.S. 2014 Electrokinetic instability near charge-selective hydrophobic surfaces. Phys. Rev. E 90 (1), 013001.CrossRefGoogle ScholarPubMed
Shi, P. 2021 Direct numerical simulation of electroconvection with thin Debye layer matching canonical experiments. Phys. Fluids 33 (3), 032015.CrossRefGoogle Scholar
Shi, P. & Liu, W. 2018 Length-dependent instability of shear electroconvective flow: from electroconvective instability to Rayleigh-Bénard instability. J. Appl. Phys. 124 (20), 204304.CrossRefGoogle Scholar
Su, Z.G., Zhang, Y.M., Luo, K. & Yi, H.L. 2020 Instability of electroconvection in viscoelastic fluids subjected to unipolar injection. Phys. Fluids 32 (10), 104102.CrossRefGoogle Scholar
Terry, P.W. 2000 Suppression of turbulence and transport by sheared flow. Rev. Mod. Phys. 72, 109–165.CrossRefGoogle Scholar
Tripathi, D., Narla, V.K. & Aboelkassem, Y. 2020 Electrokinetic membrane pumping flow model in a microchannel. Phys. Fluids 32 (8), 082004.CrossRefGoogle Scholar
Wei, P. & Ahlers, G. 2016 On the nature of fluctuations in turbulent Rayleigh-Benard convection at large Prandtl numbers. J. Fluid Mech. 802, 203–244.CrossRefGoogle Scholar
Wei, P. & Xia, K.Q. 2013 Viscous boundary layer properties in turbulent thermal convection in a cylindrical cell: the effect of cell tilting. J. Fluid Mech. 720, 140–168.CrossRefGoogle Scholar
Xu, B., Gu, Z., Liu, W., Huo, P., Zhou, Y., Rubinstein, S.M., Bazant, M.Z., Zaltzman, B., Rubinstein, I. & Deng, D. 2020 Electro-osmotic instability of concentration enrichment in curved geometries for an aqueous electrolyte. Phys. Rev. Fluids 5 (9), 091701 (R).CrossRefGoogle Scholar
Yossifon, G. & Chang, H.C. 2008 Selection of nonequilibrium overlimiting currents: universal depletion layer formation dynamics and vortex instability. Phys. Rev. Lett. 101 (25), 254501.CrossRefGoogle ScholarPubMed
Zaltzman, B. & Rubinstein, I. 2007 Electro-osmotic slip and electroconvective instability. J. Fluid Mech. 579, 173–226.CrossRefGoogle Scholar
Zheng, J., Kim, M.S., Tu, Z., Choudhury, S., Tang, T. & Archer, L.A. 2020 Regulating electrodeposition morphology of lithium: towards commercially relevant secondary li metal batteries. Chem. Soc. Rev. 49 (9), 2701–2750.CrossRefGoogle ScholarPubMed