Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T05:15:19.386Z Has data issue: false hasContentIssue false
  • English
  • Français

Critical layer and radiative instabilities in shallow-water shear flows

Published online by Cambridge University Press:  23 June 2014

Xavier Riedinger  and
Andrew D. Gilbert
Xavier Riedinger*
Affiliation:
College of Engineering, Mathematics and Physical Sciences, University of Exeter, Exeter EX4 4QF, UK
Andrew D. Gilbert
Affiliation:
College of Engineering, Mathematics and Physical Sciences, University of Exeter, Exeter EX4 4QF, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this study a linear stability analysis of shallow-water flows is undertaken for a representative Froude number 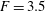$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}F=3.5$. The focus is on monotonic base flow profiles 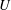$U$ without an inflection point, in order to study critical layer instability (CLI) and its interaction with radiative instability (RI). First the dispersion relation is presented for the piecewise linear profile studied numerically by Satomura (J. Meterol. Soc. Japan, vol. 59, 1981, pp. 148–167) and using WKBJ analysis an interpretation given of mode branches, resonances and radiative instability. In particular surface gravity (SG) waves can resonate with a limit mode (LM) (or Rayleigh wave), localised near the discontinuity in shear in the flow; in this piecewise profile there is no critical layer. The piecewise linear profile is then continuously modified in a family of nonlinear profiles, to show the effect of the vorticity gradient 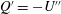$Q^{\prime } = - U^{\prime \prime }$ on the nature of the modes. Some modes remain as modes and others turn into quasi-modes (QM), linked to Landau damping of disturbances to the flow, depending on the sign of the vorticity gradient at the critical point. Thus an interpretation of critical layer instability for continuous profiles is given, as the remnant of the resonance with the LM. Numerical results and WKBJ analysis of critical layer instability and radiative instability for more general smooth profiles are provided. A link is made between growth rate formulae obtained by considering wave momentum and those found via the WKBJ approximation. Finally the competition between the stabilising effect of vorticity gradients in a critical layer and the destabilising effect of radiation (radiative instability) is studied.

JFM classification

Waves/Free-surface Flows: Critical layers Boundary Layers: Free shear layers Geophysical and Geological Flows: Shallow water flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 751 , 25 July 2014 , pp. 539 - 569
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balmforth, N. J. 1999 Shear instability in shallow water. J. Fluid Mech. 387, 97–127.Google Scholar
Balmforth, N. J., Llewellyn Smith, S. G. & Young, W. R. 2001 Disturbing vortices. J. Fluid Mech. 426, 95–133.CrossRefGoogle Scholar
Bassom, A. P. & Gilbert, A. D. 1999 The spiral wind-up and dissipation of vorticity and a passive scalar in a strained planar vortex. J. Fluid Mech. 398, 245–270.Google Scholar
Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill.Google Scholar
Berry, M. V. 1989 Uniform asymptotic smoothing of Stokes’s discontinuities. Proc. R. Soc. Lond. A 422, 7–21.Google Scholar
Billant, P. & Le Dizès, S. 2009 Waves on a columnar vortex in a strongly stratified fluid. Phys. Fluids 21, 106602.Google Scholar
Bretherton, F. P. 1966 Critical layer instability in baroclinic flows. Q. J. R. Meteorol. Soc. 92, 325–334.CrossRefGoogle Scholar
Briggs, R. J., Daugherty, J. D. & Levy, R. H. 1970 Role of Landau damping in cross-field electron beams and inviscid shear flow. Phys. Fluids 13, 421–432.Google Scholar
Broadbent, E. G. & Moore, D. W. 1979 Acoustic destabilization of vortices. Phil. Trans. R. Soc. Lond. A 290, 353–371.Google Scholar
Fjørtoft, R. 1950 Application of integral theorems in deriving criteria of stability of laminar flow and for the baroclinic circular vortex. Geophys. Publ. 17, 1–52.Google Scholar
Ford, R. 1994 The instability of an axisymmetric vortex with monotonic potential vorticity in rotating shallow water. J. Fluid Mech. 280, 303–334.Google Scholar
Glatzel, W. 1985 Sonic instabilities in supersonic shear flows. Mon. Not. R. Astron. Soc. 281, 795–821.Google Scholar
Hayashi, Y.-Y. & Young, W. R. 1987 Stable and unstable shear modes of rotating parallel flows in shallow waters. J. Fluid Mech. 184, 477–504.Google Scholar
van Heijst, G. J. F. 1991 Laboratory experiments on the tripolar vortex in a rotating fluid. J. Fluid Mech. 225, 301–331.Google Scholar
Iga, K. 1999 Critical layer instability as a resonance between a non-singular mode and continuous modes. Fluid Dyn. Res. 25, 63–86.Google Scholar
Knessl, C. & Keller, J. B. 1995 Stability of linear shear flows in shallow water. J. Fluid Mech. 303, 203–214.CrossRefGoogle Scholar
Kubokawa, A. 1985 Instability of a geostrophic front and its energetics. Geophys. Astrophys. Fluid Dyn. 33, 223–257.Google Scholar
Le Dizès, S. & Billant, P. 2009 Radiative instability in stratified vortices. Phys. Fluids 21, 096602.Google Scholar
Lin, C. C. 1945 On the stability of two-dimensional parallel flows. Q. Appl. Maths 3, 117–142.Google Scholar
Lindzen, R. S. & Barker, J. W. 1985 Instability and wave over-reflection in stably stratified shear flow. J. Fluid Mech. 151, 189–217.Google Scholar
Lindzen, R. S. & Tung, K. K. 1978 Wave over-reflection and shear instability. J. Atmos. Sci. 35, 1626–1632.2.0.CO;2>CrossRefGoogle Scholar
Mak, J., Griffiths, S. D. & Hughes, D. W. 2014 Shear instabilities in shallow water MHD. J. Fluid Mech. (in preparation).Google Scholar
Olver, F. W. J. 2010 NIST Handbook of Mathematical Functions. Cambridge University Press.Google Scholar
Papaloizou, J. C. B. & Pringle, J. E. 1987 The dynamical stability of differentially rotating disks III. Mon. Not. R. Astron. Soc. 225, 267–283.Google Scholar
Park, J. & Billant, P. 2012 Radiative instability of an anticyclonic vortex in a stratified rotating fluid. J. Fluid Mech. 707, 381–392.Google Scholar
Park, J. & Billant, P. 2013 The stably stratified Taylor–Couette flow is always unstable except for solid-body rotation. J. Fluid Mech. 725, 262–280.Google Scholar
Parras, L. & Le Dizès, S. 2010 Temporal instability modes of supersonic round jets. J. Fluid Mech. 662, 173–196.Google Scholar
Perkins, J. & Renardy, M. 1997 Stability of equatorial currents with nonzero potential vorticity. Geophys. Astrophys. Fluid Dyn. 85, 31–64.Google Scholar
Rayleigh, Lord 1880 On the stability, or instability, of certain fluid motions. Proc. Lond. Math. Soc. 11, 57–70.Google Scholar
Riedinger, X., Le Dizès, S. & Meunier, P. 2010a Viscous stability properties of a Lamb–Oseen vortex in a stratified fluid. J. Fluid Mech. 645, 255–278.CrossRefGoogle Scholar
Riedinger, X., Le Dizès, S. & Meunier, P. 2011 Radiative instability of the flow around a rotating cylinder in a stratified fluid. J. Fluid Mech. 672, 130–146.Google Scholar
Riedinger, X., Meunier, P. & Le Dizès, S. 2010b Instability of a vertical columnar vortex in a stratified fluid. Exp. Fluids 49, 673–681.Google Scholar
Rossi, L. F., Lingevitch, J. F. & Bernoff, A. J. 1997 Quasi-steady monopole and tripole attractors for relaxing vortices. Phys. Fluids 9, 2329–2338.Google Scholar
Satomura, T. 1981 An investigation of shear instability in a shallow water. J. Meterol. Soc. Japan 59, 148–167.Google Scholar
Schecter, D. A., Dubin, D. H. E., Cass, A. C., Driscoll, C. F., Lansky, I. M. & O’Neil, T. M. 2000 Inviscid damping of asymmetries on a two-dimensional vortex. Phys. Fluids 12, 2397–2412.Google Scholar
Schecter, D. A. & Montgomery, M. T. 2004 Damping and pumping of a vortex Rossby wave in a monotonic cyclone: critical layer stirring versus inertial–buoyancy wave emission. Phys. Fluids 16, 1334–1348.Google Scholar
Shepard, H. K. 1983 Decay widths for metastable states. Improved WKB approximation. Phys. Rev. D 27, 1288–1298.Google Scholar
Sutherland, B. R. 2010 Internal Gravity Waves. Cambridge University Press.Google Scholar
Takehiro, S.-I. & Hayashi, Y.-Y. 1992 Over-reflection and shear instability in a shallow-water model. J. Fluid Mech. 236, 259–279.CrossRefGoogle Scholar
Turner, M. R., Gilbert, A. D. & Bassom, A. P. 2008 Neutral modes of a two-dimensional vortex and their link to persistent cat’s eyes. Phys. Fluids 20, 027101.Google Scholar
Vanneste, J. 2013 Balance and spontaneous wave generation in geophysical flows. Annu. Rev. Fluid Mech. 45, 147–172.Google Scholar
Yim, E. & Billant, P. 2013 Spontaneous bending of a columnar vortex in stratified-rotating fluid. Bull. Am. Phys. Soc. 58 (18), 367.Google Scholar