Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T13:54:42.349Z Has data issue: false hasContentIssue false
  • English
  • Français

Creeping axisymmetric plumes with strongly temperature-dependent viscosity

Published online by Cambridge University Press:  26 March 2014

Andrew Crosby  and
John R. Lister
Andrew Crosby*
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
John R. Lister
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The structure of a steady axisymmetric thermal plume rising through a very viscous fluid with strongly temperature-dependent viscosity of the form 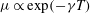$\mu \propto \exp (-\gamma T)$ is investigated. 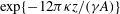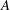An analytic asymptotic solution is derived for the fast-flowing core of the plume, which predicts that the excess centreline temperature decays exponentially as $\exp \{ - 12 \pi \kappa z/(\gamma A) \}$, where $\kappa $ is the thermal diffusivity, $z$ the height and $A$ the vertical heat flux. This rate of decay, which is found to be in good agreement with numerical simulations of the boundary-layer equations, is three times faster than that predicted by the oft-quoted model of Olson, Schubert and Anderson (J. Geophys. Res., vol. 98 (B4), 1993, pp. 6829–6844).

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Mantle convection Convection: Plumes/thermals
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 745 , 25 April 2014 , R2
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albers, M. & Christensen, U. R. 1996 The excess temperature of plumes rising from the core–mantle boundary. Geophys. Res. Lett. 23, 3567–3570.CrossRefGoogle Scholar
Christensen, U. R. 1989 Mantle rheology, constitution and convection. In Mantle Convection: Plate Tectonics and Global Dynamics (ed. Peltier, W. R.), pp. 595–655. Gordon and Breach.Google Scholar
Hauri, E. H., Whitehead, J. A. & Hart, S. R. 1994 Fluid dynamic and geochemical aspects of entrainment in mantle plumes. J. Geophys. Res. 99 (B12), 24275–24300.Google Scholar
Jellinek, A. M. & Manga, M. 2004 Links between long-lived hot spots, mantle plumes, $D^{\prime \prime }$, and plate tectonics. Rev. Geophys. 42 (3), RG3002.Google Scholar
Kerr, R. C. & Mériaux, C. 2004 Structure and dynamics of sheared mantle plumes. Geochem. Geophys. Geosyst. 5 (12), Q12009.Google Scholar
Lister, J. R., Kerr, R. C., Russell, N. J. & Crosby, A. 2011 Rayleigh–Taylor instability of an inclined buoyant viscous cylinder. J. Fluid Mech. 671, 313–338.Google Scholar
Loper, D. E. & Stacey, F. D. 1983 The dynamical and thermal structure of deep mantle plumes. Phys. Earth Planet. Inter. 33, 304–317.CrossRefGoogle Scholar
Morgan, W. J. 1971 Convection plumes in the lower mantle. Nature 230, 42–43.Google Scholar
Morris, S.1980 An asymptotic method for determining the transport of heat and matter by creeping flows with strongly variable viscosity. PhD thesis, Johns Hopkins University.Google Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234 (1196), 1–23.Google Scholar
Olson, P., Schubert, G. & Anderson, C. 1993 Structure of axisymmetric mantle plumes. J. Geophys. Res. 98 (B4), 6829–6844.Google Scholar
Schubert, G., Turcotte, D. L. & Olson, P. 2001 Mantle Convection in the Earth and Planets. Cambridge University Press.CrossRefGoogle Scholar
Steinberger, B. & Antretter, M. 2006 Conduit diameter and buoyant rising speed of mantle plumes: implications for the motion of hot spots and shape of plume conduits. Geochem. Geophys. Geosyst. 7 (11), Q11018.Google Scholar
Whittaker, R. J. & Lister, J. R. 2006 Steady axisymmetric creeping plumes above a planar boundary. Part 1. A point source. J. Fluid Mech. 567, 361–378.Google Scholar
Yuen, D. A. & Schubert, G. 1976 Mantle plumes: a boundary layer approach for Newtonian and non-Newtonian temperature-dependent rheologies. J. Geophys. Res. 81 (14), 2499–2510.Google Scholar