Article contents
Counter-hairpin vortices in the turbulent wake of a sharp trailing edge
Published online by Cambridge University Press: 28 November 2011
Abstract
The unsteady organization and evolution of coherent structures within the turbulent boundary layer and subsequent wake of the sharp symmetric trailing edge of a NACA0012 aerofoil are investigated. The experiments are conducted in an open test-section wind tunnel at  based on the aerofoil chord and
based on the aerofoil chord and 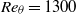 based on the boundary layer momentum thickness. An initial characterization of the flow field using two-component particle image velocimetry (PIV) is followed by the investigation of the unsteady organization and evolution of coherent structures by time-resolved three-dimensional PIV based on a tomographic approach (Tomo-PIV). The inspection of the turbulent boundary layer prior to the trailing edge in the region between 0.15 and
based on the boundary layer momentum thickness. An initial characterization of the flow field using two-component particle image velocimetry (PIV) is followed by the investigation of the unsteady organization and evolution of coherent structures by time-resolved three-dimensional PIV based on a tomographic approach (Tomo-PIV). The inspection of the turbulent boundary layer prior to the trailing edge in the region between 0.15 and 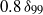 demonstrated streaks of low- and high-speed flow, while the low-speed streaks are observed to be more coherent along with strong interaction with hairpin-type vortical structures similar to a turbulent boundary layer at zero pressure gradient. The wake region demonstrated gradual deterioration of both the low- and the high-speed streaks with downstream progress. However, the low-speed streaks are observed to lose their coherence at a faster rate relative to the high-speed streaks as the turbulent flow develops towards the far wake. The weakening of the low-speed streaks is due to the disappearance of the viscous sublayer after the trailing edge and gradual mixing through the transport of the remaining low-speed flow towards the free stream. This transport of low-speed flow is performed by the ejection events induced by the hairpin vortices as they also persist into the developing wake. The higher persistence of the high-speed streaks is associated with counter-hairpin vortical activities as they oppose the deterioration of the high-speed streaks by frequently sweeping the high-speed flow towards the wake centreline. These vortical structures are regarded as counter-hairpin vortices as they exhibit opposite characteristics relative to the hairpin vortices of a turbulent boundary layer. They are topologically similar to the hairpins as they appear to be U-shaped but with inverted orientation, as the spanwise portion is in the vicinity of the wake centreline and the legs are inclined at an approximately
demonstrated streaks of low- and high-speed flow, while the low-speed streaks are observed to be more coherent along with strong interaction with hairpin-type vortical structures similar to a turbulent boundary layer at zero pressure gradient. The wake region demonstrated gradual deterioration of both the low- and the high-speed streaks with downstream progress. However, the low-speed streaks are observed to lose their coherence at a faster rate relative to the high-speed streaks as the turbulent flow develops towards the far wake. The weakening of the low-speed streaks is due to the disappearance of the viscous sublayer after the trailing edge and gradual mixing through the transport of the remaining low-speed flow towards the free stream. This transport of low-speed flow is performed by the ejection events induced by the hairpin vortices as they also persist into the developing wake. The higher persistence of the high-speed streaks is associated with counter-hairpin vortical activities as they oppose the deterioration of the high-speed streaks by frequently sweeping the high-speed flow towards the wake centreline. These vortical structures are regarded as counter-hairpin vortices as they exhibit opposite characteristics relative to the hairpin vortices of a turbulent boundary layer. They are topologically similar to the hairpins as they appear to be U-shaped but with inverted orientation, as the spanwise portion is in the vicinity of the wake centreline and the legs are inclined at an approximately 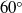 to the wake axis in the downstream direction demonstrating a strain-dominated topology. The counter-hairpin vortices are partially wrapped around the high-speed streaks and contribute to the wake development by transporting high-speed flow towards the wake centreline. Similar to the hairpin vortices of a turbulent boundary layer, the occurrence of a complete counter-hairpin vortex is occasional while its derivatives (portions of spanwise or quasi-streamwise vortices) are more frequently observed. Therefore, a pattern recognition algorithm is applied to establish characterization based on an ensemble-averaged counter-hairpin vortex. The formation of the counter-hairpin vortices is due to an additional degree of interaction between the low- and high-speed streaks after the trailing edge across the wake centreline. The shear layer produced along the wake centreline by neighbouring low- and high-speed streaks promotes the formation of spanwise vortices that form the counter-hairpin vortices by connection to quasi-streamwise vortices. Finally, a conceptual model is proposed to depict the three-dimensional unsteady organization and evolution of coherent structures in the wake region based on the hairpin and counter-hairpin vortex signatures.
to the wake axis in the downstream direction demonstrating a strain-dominated topology. The counter-hairpin vortices are partially wrapped around the high-speed streaks and contribute to the wake development by transporting high-speed flow towards the wake centreline. Similar to the hairpin vortices of a turbulent boundary layer, the occurrence of a complete counter-hairpin vortex is occasional while its derivatives (portions of spanwise or quasi-streamwise vortices) are more frequently observed. Therefore, a pattern recognition algorithm is applied to establish characterization based on an ensemble-averaged counter-hairpin vortex. The formation of the counter-hairpin vortices is due to an additional degree of interaction between the low- and high-speed streaks after the trailing edge across the wake centreline. The shear layer produced along the wake centreline by neighbouring low- and high-speed streaks promotes the formation of spanwise vortices that form the counter-hairpin vortices by connection to quasi-streamwise vortices. Finally, a conceptual model is proposed to depict the three-dimensional unsteady organization and evolution of coherent structures in the wake region based on the hairpin and counter-hairpin vortex signatures.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
Ghaemi and Scarano supplementary material
Movie 1. Time-resolved evolution of the low and high speed streaks and the vortical structures in the turbulent boundary layer upstream of the trailing-edge at Reθ= 1300 measured using the Tomo-PIV technique. The original measurement frequency of 2700 Hz has been increased in this movie to 27000 Hz using the advection equation following Scarano & Moore (2011). The visualization shows significant accumulation of the vortical structures around the low speed streaks.
Ghaemi and Scarano supplementary material
Movie 1. Time-resolved evolution of the low and high speed streaks and the vortical structures in the turbulent boundary layer upstream of the trailing-edge at Reθ= 1300 measured using the Tomo-PIV technique. The original measurement frequency of 2700 Hz has been increased in this movie to 27000 Hz using the advection equation following Scarano & Moore (2011). The visualization shows significant accumulation of the vortical structures around the low speed streaks.
Ghaemi and Scarano supplementary material
Movie 2. Time-resolved Tomo-PIV visualization of the low and high speed streaks and the vortical structures in the immediate wake of the sharp symmetric trailing-edge of NACA 0012 at Reθ= 1300. The temporal resolution has been increased in this movie to 27000 Hz using the advection equation following Scarano & Moore (2011). Vortical activities are observed around both the low and the high speed streaks.
Ghaemi and Scarano supplementary material
Movie 2. Time-resolved Tomo-PIV visualization of the low and high speed streaks and the vortical structures in the immediate wake of the sharp symmetric trailing-edge of NACA 0012 at Reθ= 1300. The temporal resolution has been increased in this movie to 27000 Hz using the advection equation following Scarano & Moore (2011). Vortical activities are observed around both the low and the high speed streaks.
- 46
- Cited by


