Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-23T08:43:18.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Counter-gradient heat transport in two-dimensional turbulent Rayleigh–Bénard convection

Published online by Cambridge University Press:  22 November 2013

Yong-Xiang Huang  and
Quan Zhou
Yong-Xiang Huang
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics, and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, PR China
Quan Zhou*
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics, and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

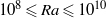We present high-resolution numerical investigations of heat transport by two-dimensional (2D) turbulent Rayleigh–Bénard (RB) convection over the Rayleigh number range $1{0}^{8} \leqslant Ra\leqslant 1{0}^{10} $ and the Prandtl number range 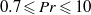$0. 7\leqslant Pr\leqslant 10$. We find that there exists strong counter-gradient local heat flux with magnitude much larger than the global Nusselt number $Nu$ of the system. Two mechanisms for generating counter-gradient heat transport are identified: one is due to the bulk dynamics and the other is due to the competition between the corner-flow rolls and the large-scale circulation (LSC). While the magnitude of the former is found to increase with increasing Prandtl number, that of the latter maximizes at medium 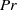$Pr$. We further reveal that the corner–LSC competition leads to the anomalous 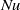$Nu$–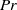$Pr$ relation in 2D RB convection, i.e. 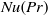$Nu(Pr)$ minimizes, rather than maximizes as in the three-dimensional cylindrical case, at 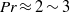$Pr\approx 2\sim 3$ for moderate 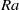$Ra$.

JFM classification

Convection: Convection Turbulent Flows: Turbulent convection Turbulent Flows: Turbulent Flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 737 , 25 December 2013 , R3
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Ahlers, G. & Xu, X.-C. 2001 Prandtl-number dependence of heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 86, 3320–3323.CrossRefGoogle ScholarPubMed
Breuer, M., Wessling, S., Schmalzl, J. & Hansen, U. 2004 Effect of inertia in Rayleigh–Bénard convection. Phys. Rev. E 69, 026302.Google Scholar
Calzavarini, E., Lohse, D., Toschi, F. & Tripiccione, R. 2005 Rayleigh and Prandtl number scaling in the bulk of Rayleigh–Bénard convection. Phys. Fluids 17, 055107.Google Scholar
Chandra, M. & Verma, M. K. 2011 Dynamics and symmetries of flow reversals in turbulent convection. Phys. Rev. E 83, 067303.CrossRefGoogle ScholarPubMed
Chandra, M. & Verma, M. K. 2013 Flow reversals in turbulent convection via vortex reconnections. Phys. Rev. Lett. 110, 114503.CrossRefGoogle ScholarPubMed
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.CrossRefGoogle ScholarPubMed
Ching, E. S. C., Guo, H., Shang, X.-D., Tong, P. & Xia, K.-Q. 2004 Extraction of plumes in turbulent thermal convection. Phys. Rev. Lett. 93, 124501.Google Scholar
E, W. & Liu, J.-G. 1996 Essentially compact schemes for unsteady viscous incompressible flows. J. Comput. Phys. 126, 122–138.Google Scholar
Gasteuil, Y., Shew, W. L., Gibert, M., Chilla, F., Castaing, B. & Pinton, J.-F. 2007 Lagrangian temperature, velocity, and local heat flux measurement in Rayleigh–Bénard convection. Phys. Rev. Lett. 99, 234302.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle ScholarPubMed
He, X.-Z., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2013 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.Google Scholar
Huang, S.-D., Kaczorowski, M., Ni, R & Xia, K.-Q. 2013 Confinement-induced heat-transport enhancement in turbulent thermal convection. Phys. Rev. Lett. 111, 104501.Google Scholar
Johnston, H. & Doering, C. R. 2009 Comparison of temperature thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102, 064501.Google Scholar
Kerr, R. M. & Herring, J. 2000 Prandtl number dependence of Nusselt number in direct numerical simulations. J. Fluid Mech. 491, 325–344.Google Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5, 1374–1389.Google Scholar
Lakkaraju, R., Stevens, R. J. A. M., Oresta, P., Verzicco, R., Lohse, D. & Prosperetti, A. 2013 Heat transport in bubbling turbulent Rayleigh–Bénard convection. Proc. Natl Acad. Sci. USA 110 (23), 9237–9242.CrossRefGoogle Scholar
Liu, J.-G., Wang, C. & Johnston, H. 2003 A fourth order scheme for incompressible Boussinesq equations. J. Sci. Comput. 18, 253–285.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Niemela, J. J. & Sreenivasan, K. R. 2003 Confined turbulent convection. J. Fluid Mech. 481, 355–384.Google Scholar
van der Poel, E. P., Stevens, R. J. A. M. & Lohse, D. 2011 Connecting flow structures and heat flux in turbulent Rayleigh–Bénard convection. Phys. Rev. E 84, 045303(R).CrossRefGoogle ScholarPubMed
ver der Poel, E. P., Stevens, R. J. A. M., Sugiyama, K. & Lohse, D. 2012 Flow states in two-dimensional Rayleigh–Bénard convection as a function of aspect-ratio and Rayleigh number. Phys. Fluids 24, 085104.Google Scholar
Roche, P.-E., Castaing, B., Chabaud, B. & Hébral, B. 2002 Prandtl and Rayleigh numbers dependences in Rayleigh–Bénard convection. Europhys. Lett. 58, 693–698.Google Scholar
Seychelles, F., Amarouchene, Y., Bessafi, M. & Kellay, H. 2008 Thermal convection and emergence of isolated vortices in soap bubbles. Phys. Rev. Lett. 100, 144501.Google Scholar
Seychelles, F., Ingremeau, F., Pradere, C. & Kellay, H. 2010 From intermittent to nonintermittent behaviour in two-dimensional thermal convection in a soap bubble. Phys. Rev. Lett. 105, 264502.Google Scholar
Shang, X.-D., Qiu, X.-L., Tong, P. & Xia, K.-Q. 2003 Measured local heat transport in turbulent Rayleigh-Bénard convection. Phys. Rev. Lett. 90, 074501.CrossRefGoogle ScholarPubMed
Shang, X.-D., Qiu, X.-L., Tong, P. & Xia, K.-Q. 2004 Measurements of the local convective heat flux in turbulent Rayleigh-Bénard convection. Phys. Rev. E 70, 026308.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.CrossRefGoogle Scholar
Silano, G., Sreenivasan, K. R. & Verzicco, R. 2010 Numerical simulations of Rayleigh–Bénard convection for Prandtl numbers between $1{0}^{- 1} $ and $1{0}^{4} $ and Rayleigh numbers between $1{0}^{5} $ and $1{0}^{9} $ . J. Fluid Mech. 662, 409–446.Google Scholar
Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011 Prandtl and Rayleigh number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid Mech. 688, 31–43.Google Scholar
Sugiyama, K., Calzavarini, E., Grossmann, S. & Lohse, D. 2009 Flow organization in two-dimensional non-Oberbeck-Boussinesq Rayleigh–Bénard convection in water. J. Fluid Mech. 637, 105–135.CrossRefGoogle Scholar
Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T.-S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105, 034503.Google Scholar
Urban, P., Schmoranzer, D., Hanzelka, P., Sreenivsan, K. R. & Skrbek, L. 2013 Anomalous heat transport and condensation in convection of cryogenic helium. Proc. Natl Acad. Sci. USA 110 (20), 8036–8039.Google Scholar
Verzicco, R. & Camussi, R. 1999 Prandtl number effects in convective turbulence. J. Fluid Mech. 383, 55–73.Google Scholar
Whitehead, J. P. & Doering, C. R. 2011 Ultimate state of two-dimensional Rayleigh–Bénard convection between free-slip fixed-temperature boundaries. Phys. Rev. Lett. 106, 244501.Google Scholar
Xia, K.-Q. 2013 Current trends and future directions in turbulent thermal convection. Theor. Appl. Mech. Lett. 3, 04200z.Google Scholar
Xia, K.-Q., Lam, S. & Zhou, S.-Q. 2002 Heat-flux measurement in high-Prandtl-number turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 88, 064501.Google Scholar
Zhang, J. & Wu, X.-L. 2005 Velocity intermittency in a buoyancy subrange in a two-dimensional soap film convection experiment. Phys. Rev. Lett. 94, 234501.Google Scholar
Zhang, J., Wu, X.-L. & Xia, K.-Q. 2005 Density fluctuations in strongly stratified two-dimensional turbulence. Phys. Rev. Lett. 94, 174503.Google Scholar
Zhou, Q. 2013 Temporal evolution and scaling of mixing in two-dimensional Rayleigh–Taylor turbulence. Phys. Fluids 25, 085107.Google Scholar
Zhou, Q., Liu, B.-F., Li, C.-M. & Zhong, B.-C. 2012 Aspect ratio dependence of heat transport by turbulent Rayleigh–Bénard convection in rectangular cells. J. Fluid Mech. 710, 260–276.Google Scholar
Zhou, Q., Lu, H., Liu, B.-F. & Zhong, B.-C. 2013 Measurements of heat transport by turbulent Rayleigh–Bénard convection in rectangular cells of widely varying aspect ratios. Sci. China-Phys. Mech. Astron. 56, 989–994.Google Scholar
Zhou, Q., Stevens, R. J. A. M., Sugiyama, K., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl–Blasius temperature and velocity boundary-layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 664, 297–312.Google Scholar
Zhou, Q., Sugiyama, K., Stevens, R. J. A. M., Grossmann, S., Lohse, D. & Xia, K.-Q. 2011 Horizontal structures of velocity and temperature boundary layers in two-dimensional numerical turbulent -Bénard convection. Phys. Fluids 23, 125104.Google Scholar

Huang and Zhou supplementary movie

Movie of the instantaneous temperature (color) and velocity (arrows) fields for $Ra=3\times10^8$ and $Pr=4.38$. Right panel: The corresponding movie of the local heat flux field (color). The black solid lines mark the streamlines of $\psi=0$, which can roughly distinguish the regions of the corner-flow rolls and the LSC."

Download Huang and Zhou supplementary movie(Video)
Video 17.1 MB