Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-25T07:36:51.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Co-rotating Taylor–Couette flow enclosed by stationary disks

Published online by Cambridge University Press:  28 January 2013

M. Heise ,
Ch. Hoffmann ,
Ch. Will ,
S. Altmeyer ,
J. Abshagen  and
G. Pfister
M. Heise*
Affiliation:
Institut für Experimentelle und Angewandte Physik, Universität Kiel, D-24098 Kiel, Germany
Ch. Hoffmann
Affiliation:
Institut für Theoretische Physik, Universität des Saarlandes, D-66123 Saarbrücken, Germany
Ch. Will
Affiliation:
Institut für Experimentelle und Angewandte Physik, Universität Kiel, D-24098 Kiel, Germany
S. Altmeyer
Affiliation:
Institut für Theoretische Physik, Universität des Saarlandes, D-66123 Saarbrücken, Germany
J. Abshagen
Affiliation:
Institut für Experimentelle und Angewandte Physik, Universität Kiel, D-24098 Kiel, Germany
G. Pfister
Affiliation:
Institut für Experimentelle und Angewandte Physik, Universität Kiel, D-24098 Kiel, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

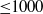We report results of a combined numerical and experimental study on axisymmetric and non-axisymmetric flow states in a finite-length, co-rotating Taylor–Couette system in the Taylor vortex regime but also in the Rayleigh stable regime for moderate Reynolds numbers (${\leq }1000$). We found the dominant boundary-driven axisymmetric circulation to play a crucial role in the mode selection and the bifurcation behaviour in this flow. A sequence of partially hysteretic transitions to other axisymmetric multi-cell flow states is observed. Furthermore, we observed spiral states bifurcating via a supercritical Hopf bifurcation out of these multi-cell states which strongly determine the shape of the spiral. Finally, an excellent agreement between experimental and numerical results of the full Navier–Stokes equations is found.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Vortex Flows: Vortex Flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , R4
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abshagen, J., Heise, M., Pfister, G. & Mullin, T. 2010 Multiple localized states in centrifugally stable rotating flow. Phys. Fluids 22, 1–4.Google Scholar
Abshagen, J., Langenberg, J., Pfister, G., Mullin, T., Tavener, S. J. & Cliffe, K. A. 2004 Taylor–Couette flow with independently rotating end plates. J. Theor. Comput. Fluid Dyn. 18, 129–136.CrossRefGoogle Scholar
Altmeyer, S. & Hoffmann, Ch. 2010 Secondary bifurcation of mixed-cross-spirals connecting travelling wave solutions. New J. Phys. 12 (11), 113035.CrossRefGoogle Scholar
Altmeyer, S., Hoffmann, Ch., Heise, M., Abshagen, J., Pinter, A., Lücke, M. & Pfister, G. 2010 End wall effects on the transitions between Taylor vortices and spiral vortices. Phys. Rev. E 81 (6), 066313.Google Scholar
Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.Google Scholar
Avila, M. 2012 Stability and angular-momentum transport of fluid flows between corotating cylinders. Phys. Rev. Lett. 108, 124501.Google Scholar
Avila, M., Grimes, M., Lopez, J. M. & Marques, F. 2008 Global endwall effects on centrifugally stable flows. Phys. Fluids 20, 104104.CrossRefGoogle Scholar
Benjamin, T. B. 1978 Bifurcation phenomena in steady flows of a viscous fluid. I. Theory.. Proc. R. Soc. Lond. A 359, 1–26.Google Scholar
Benjamin, T. B. 1978 Bifurcation phenomena in steady flows of a viscous fluid. II. Experiments. Proc. R. Soc. Lond. A 359, 27–43.Google Scholar
Benjamin, T. B. & Mullin, T. 1981 Anomalous modes in the Taylor experiment. Proc. R. Soc. Lond. A 377, 221–249.Google Scholar
Büchel, P., Lücke, M., Roth, D. & Schmitz, R. 1996 Pattern selection in the absolutely unstable regime as a nonlinear eigenvalue problem: Taylor vortices in axial flow. Phys. Rev. E 53, 4764–4777.CrossRefGoogle ScholarPubMed
Burin, M., Ji, H., Schartman, E., Cutler, R., Heitzenroeder, P., Liu, W., Morris, L. & Raftopolous, S. 2006 Reduction of Ekman circulation within Taylor–Couette flow. Exp. Fluids 40 (6), 962–966.CrossRefGoogle Scholar
Cliffe, K. A., Kobine, J. J. & Mullin, T. 1992 The role of anomalous modes in Taylor–Couette flow. Proc. R. Soc. Lond. A 439 (1906), 341–357.Google Scholar
Cross, M. C. & Hohenberg, P. C. 1993 Pattern formation outside of equilibrium. Rev. Mod. Phys. 65 (3), 851.Google Scholar
Czarny, O., Serre, E., Bontoux, P. & Lueptow, R. M. 2003 Interaction between Ekman pumping and the centrifugal instability in Taylor–Couette flow. Phys. Fluids 15, 467.Google Scholar
Duschl, W. J. & Britsch, M. 2006 A gravitational instability-driven viscosity in self-gravitating accretion disks. Astrophys. J. Lett. 653 (2), 89–92.Google Scholar
van Gils, D. P. M., Huisman, S. G., Bruggert, G.-W., Sun, Ch. & Lohse, D. 2011 Torque scaling in turbulent Taylor–Couette flow with co- and counterrotating cylinders. Phys. Rev. Lett. 106, 024502.CrossRefGoogle ScholarPubMed
Hegseth, J. J., Baxter, G. W. & Andereck, C. D. 1996 Bifurcation from Taylor vortices between corotating concentric cylinders. Phys. Rev. E 53, 507–521.CrossRefGoogle ScholarPubMed
Heise, M., Abshagen, J., Hochstrate, K., Küter, D., Pfister, G. & Hoffmann, Ch. 2008a Localized spirals in Taylor–Couette flow. Phys. Rev. E 77, 026202.Google Scholar
Heise, M., Hochstrate, K., Abshagen, J. & Pfister, G. 2009 Spirals vortices in Taylor–Couette flow with rotating endwalls. Phys. Rev. E 80 (4), 045301.Google Scholar
Heise, M., Hoffmann, Ch., Abshagen, J., Pinter, A., Pfister, G. & Lücke, M. 2008b Stabilization of domain walls between traveling waves by nonlinear mode coupling in Taylor–Couette flow. Phys. Rev. Lett. 100 (6), 064501.Google Scholar
Hirt, C. W., Nichols, B. D. & Romero, N. C. 1975 SOLA: a numerical solution algorithm for transient fluid flows. NASA STI/Recon Tech. Rep. N 75, 32418.Google Scholar
Hollerbach, R. & Fournier, A. 2004 End-effects in rapidly rotating cylindrical Taylor–Couette flow. In MHD Couette Flows: Experiments and Models, vol. 733, pp. 114–121.Google Scholar
Hollerbach, R. & Rüdiger, G. 2005 New type of magnetorotational instability in cylindrical Taylor–Couette flow. Phys. Rev. Lett. 95 (12), 124501.Google Scholar
Ji, H., Burin, M., Schartman, E. & Goodman, J. 2006 Hydrodynamic turbulence cannot transport angular momentum effectively in astrophysical disks. Nature 444 (7117), 343–346.CrossRefGoogle ScholarPubMed
Langford, W. F., Tagg, R., Kostelich, E. J., Swinney, H. L. & Golubitsky, M. 1988 Primary instabilities and bicriticality in flow between counter rotating cylinders. Phys. Fluids 31, 776–785.Google Scholar
Mullin, T. 1982 Mutations of steady cellular flows in the Taylor experiment. J. Fluid Mech. 121, 207–218.Google Scholar
Nagata, M. 1988 On wavy instabilities of the Taylor-vortex flow between corotating cylinders. J. Fluid Mech. 88, 585.Google Scholar
Paoletti, M. S. & Lathrop, D. P. 2011 Angular momentum transport in turbulent flow between independently rotating cylinders. Phys. Rev. Lett. 106, 024501.Google Scholar
Peyret, R. & Taylor, T. D. 1985 Computational Methods for Fluid Flow. Springer.Google Scholar
Pinter, A., Lücke, M. & Hoffmann, Ch. 2003 Spiral and Taylor vortex fronts and pulses in axial through flow. Phys. Rev. E 67, 026318.CrossRefGoogle ScholarPubMed
Recktenwald, A., Lücke, M. & Müller, H. W. 1993 Taylor vortex formation in axial through-flow: linear and weakly nonlinear analysis. Phys. Rev. E 48, 4444–4454.Google Scholar
Schartman, E., Ji, H. & Burin, M. 2009 Development of a Couette–Taylor flow device with active minimization of secondary circulation. Rev. Sci. Instrum. 80, 024501.CrossRefGoogle ScholarPubMed
Stefani, F., Gundrum, T., Gerbeth, G., Rüdiger, G., Schultz, M., Szklarski, J. & Hollerbach, R. 2006 Experimental evidence for magnetorotational instability in a Taylor–Couette flow under the influence of a helical magnetic field. Phys. Rev. Lett. 97 (18), 184502.Google Scholar
Tagg, R. 1994 The Couette-Taylor problem. Nonlinear Sci. Today 4 (3), 1–25.Google Scholar
Tavener, S. J. & Cliffe, K. A. 1991 Primary flow exchange mechanisms in the Taylor apparatus applying impermeable stress-free boundary conditions. IMA J Appl. Maths 46, 165–199.Google Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 223, 289–343.Google Scholar