We investigate the convergence behaviour of a cylindrical, fast magnetohydrodynamic (MHD) shock wave in a neutrally ionized gas collapsing onto an axial line current that generates a power law in time, azimuthal magnetic field. The analysis is done within the framework of a modified version of ideal MHD for an inviscid, non-dissipative, neutrally ionized compressible gas. The time variation of the magnetic field is tuned such that it approaches zero at the instant that the shock reaches the axis. This configuration is motivated by the desire to produce a finite magnetic field at finite shock radius but a singular gas pressure and temperature at the instant of shock impact. Our main focus is on the variation with shock radius $r$, as 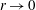$r\rightarrow 0$, of the shock Mach number 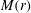$M(r)$ and pressure behind the shock 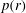$p(r)$ as a function of the magnetic field power-law exponent 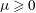${\it\mu}\geqslant 0$, where 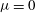${\it\mu}=0$ gives a constant-in-time line current. The flow problem is first formulated using an extension of geometrical shock dynamics (GSD) into the time domain to take account of the time-varying conditions ahead of the converging shock, coupled with appropriate shock-jump conditions for a fast, symmetric MHD shock. This provides a pair of ordinary differential equations describing both 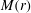$M(r)$ and the time evolution on the shock, as a function of $r$, constrained by a collapse condition required to achieve tuned shock convergence. Asymptotic, analytical results for $M(r)$ and 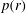$p(r)$ are obtained over a range of 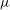${\it\mu}$ for general 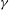${\it\gamma}$, and for both small and large $r$. In addition, numerical solutions of the GSD equations are performed over a large range of $r$, for selected parameters using 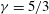${\it\gamma}=5/3$. The accuracy of the GSD model is verified for some cases using direct numerical solution of the full, radially symmetric MHD equations using a shock-capturing method. For the GSD solutions, it is found that the physical character of the shock convergence to the axis is a strong function of 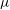${\it\mu}$. For 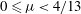$0\leqslant {\it\mu}<4/13$, 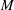$M$ and 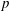$p$ both approach unity at shock impact 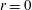$r=0$ owing to the dominance of the strong magnetic field over the amplifying effects of geometrical convergence. When 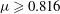${\it\mu}\geqslant 0.816$ (for 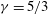${\it\gamma}=5/3$), geometrical convergence is dominant and the shock behaves similarly to a converging gas dynamic shock with singular 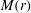$M(r)$ and 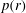$p(r)$, 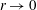$r\rightarrow 0$. For 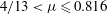$4/13<{\it\mu}\leqslant 0.816$ three distinct regions of 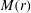$M(r)$ variation are identified. For each of these 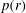$p(r)$ is singular at the axis.