Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T23:08:24.390Z Has data issue: false hasContentIssue false
  • English
  • Français

Convective shutdown in a porous medium at high Rayleigh number

Published online by Cambridge University Press:  19 February 2013

Duncan R. Hewitt ,
Jerome A. Neufeld  and
John R. Lister
Duncan R. Hewitt*
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
Jerome A. Neufeld
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK Department of Earth Sciences, University of Cambridge, Downing Street, Cambridge CB2 3EQ, UK BP Institute, University of Cambridge, Bullard Laboratories, Madingley Road, Cambridge CB3 0EZ, UK
John R. Lister
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

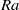Convection in a closed domain driven by a dense buoyancy source along the upper boundary soon starts to wane owing to the increase of the average interior density. In this paper, theoretical and numerical models are developed of the subsequent long period of shutdown of convection in a two-dimensional porous medium at high Rayleigh number $\mathit{Ra}$. The aims of this paper are twofold. Firstly, the relationship between this slowly evolving ‘one-sided’ shutdown system and the statistically steady ‘two-sided’ Rayleigh–Bénard (RB) cell is investigated. Numerical measurements of the Nusselt number 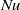$\mathit{Nu}$ from an RB cell (Hewitt et al., Phys. Rev. Lett., vol. 108, 2012, 224503) are very well described by the simple parametrization 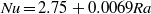$\mathit{Nu}= 2. 75+ 0. 0069\mathit{Ra}$. This parametrization is used in theoretical box models of the one-sided shutdown system and found to give excellent agreement with high-resolution numerical simulations of this system. The dynamical structure of shutdown can also be accurately predicted by measurements from an RB cell. Results are presented for a general power-law equation of state. Secondly, these ideas are extended to model more complex physical systems, which comprise two fluid layers with an equation of state such that the solution that forms at the (moving) interface is more dense than either layer. The two fluids are either immiscible or miscible. Theoretical box models compare well with numerical simulations in the case of a flat interface between the fluids. Experimental results from a Hele-Shaw cell and numerical simulations both show that interfacial deformation can dramatically enhance the convective flux. The applicability of these results to the convective dissolution of geologically sequestered 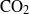${\mathrm{CO} }_{2} $ in a saline aquifer is discussed.

JFM classification

Convection: Convection Convection: Convection in porous media Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 719 , 25 March 2013 , pp. 551 - 586
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Backhaus, S., Turitsyn, K. & Ecke, R. E. 2011 Convective instability and mass transport of diffusion layers in a Hele-Shaw geometry. Phys. Rev. Lett. 106, 104501.CrossRefGoogle Scholar
Bickle, M., Chadwick, A., Huppert, H. E., Hallworth, M. A. & Lyle, S. 2007 Modelling carbon dioxide accumulation at Sleipner: implications for underground carbon storage. Earth Planet. Sci. Lett. 255, 164–176.CrossRefGoogle Scholar
Cheng, P. 1978 Heat transfer in geothermal systems. Adv. Heat Transfer 14, 1–105.Google Scholar
Duffy, C. J. & Al-Hassan, S. 1988 Groundwater circulation in a closed desert basin: topographic scaling and climatic forcing. Water Resour. Res. 24, 1675–1688.CrossRefGoogle Scholar
Ennis-King, J. P. & Paterson, L. 2005 Role of convective mixing in the long-term storage of carbon dioxide in deep saline formations. SPE J. 10 (3), 349–356.CrossRefGoogle Scholar
Fernandez, J., Kurowski, P., Petitjeans, P. & Meiburg, E. 2002 Density-driven unstable flows of miscible fluids in a Hele-Shaw cell. J. Fluid Mech. 451, 239–260.CrossRefGoogle Scholar
Gilfillan, S. M. V., Sherwood Lollar, B., Holland, G., Blagburn, D., Stevens, S., Schoell, M., Cassidy, M., Ding, Z., Zhou, Z., Lacrampe-Couloume, G. & Ballentine, C. J. 2009 Solubility trapping in formation water as dominant ${\mathrm{CO} }_{2} $ sinks in natural gas fields. Nature 458, 614–618.CrossRefGoogle Scholar
Goldstein, B., Hiriart, G., Bertani, R., Bromley, C., Gutiérrez-Negrín, L., Huenges, E., Muraoka, H., Ragnarsson, A., Tester, J. & Zui, V. 2011 Geothermal energy. In Renewable Energy Sources and Climate Change Mitigation: Special Report of the IPCC, pp. 401–436. Cambridge University Press.CrossRefGoogle Scholar
Graham, M. D. & Steen, P. H. 1994 Plume formation and resonant bifurcations in porous-media convection. J. Fluid Mech. 272, 67–89.CrossRefGoogle Scholar
Hassanzadeh, H., Pooladi-Darvish, M. & Keith, D. W. 2006 Stability of a fluid in a horizontal saturated porous layer: effect of nonlinear concentration profile, initial and boundary conditions. Transp. Porous Med. 65, 193–211.CrossRefGoogle Scholar
Hassanzadeh, H., Pooladi-Darvish, M. & Keith, D. W. 2007 Scaling behaviour of convective mixing, with application to geological storage of ${\mathrm{CO} }_{2} $ . AIChE J. 53, 1121–1131.CrossRefGoogle Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2012 Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 108, 224503.CrossRefGoogle Scholar
Hill, J. M. 1987 One-Dimensional Stefan Problems: An Introduction. Longman.Google Scholar
Howard, L. N. 1964 Convection at high Rayleigh number. In Applied Mechanics, Proceedings of 11th International Congress of Applied Mathematics (ed. Görtler, H. & Sorger, P.). pp. 1109–1115. Springer.Google Scholar
Huppert, H. E. 1989 Phase changes following the initiation of a hot turbulent flow over a cold solid surface. J. Fluid Mech. 198, 293–319.CrossRefGoogle Scholar
Huppert, H. E. & Sparks, R. S. J. 1988a The generation of granitic magmas by intrusion of basalt into continental crust. J. Petrol. 29 (3), 599–624.CrossRefGoogle Scholar
Huppert, H. E. & Sparks, R. S. J. 1988b Melting the roof of a chamber containing a hot, turbulently convecting fluid. J. Fluid Mech. 188, 107–131.CrossRefGoogle Scholar
Kimura, S., Schubert, G. & Strauss, J. M. 1986 Route to chaos in porous-medium thermal convection. J. Fluid Mech. 166, 305–324.CrossRefGoogle Scholar
van der Meer, B. 2005 Carbon dioxide storage in natural gas reservoirs. Oil Gas Sci. Technol. 60, 527–536.CrossRefGoogle Scholar
Metz, B., Davidson, O., de Coninck, H. C., Loos, M. & Meyer, L. 2005 Carbon Dioxide Capture and Storage: Special Report of the IPCC. Cambridge University Press.Google Scholar
Neufeld, J. A., Hesse, M. A., Riaz, A., Hallworth, M. A., Tchelepi, H. A. & Huppert, H. E. 2010 Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37, 22404.CrossRefGoogle Scholar
Neufeld, J. A., Vella, D., Huppert, H. E. & Lister, J. R. 2011 Leakage from gravity currents in a porous medium. Part I. A localized sink. J. Fluid Mech. 666, 391–413.CrossRefGoogle Scholar
Nield, D. A. & Bejan, A. 2006 Convection in Porous Media, 3rd edn. Springer.Google Scholar
Orr, F. M. Jr. 2009 Onshore geologic storage of ${\mathrm{CO} }_{2} $ . Science 325, 1656–1658.CrossRefGoogle Scholar
Otero, J., Dontcheva, L. A., Johnston, H., Worthing, R. A., Kurganov, A., Petrova, G. & Doering, C. R. 2004 High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 500, 263–281.CrossRefGoogle Scholar
Pau, G. S. H., Bell, J. B., Pruess, K., Almgren, A. S., Lijewski, M. J. & Zhang, K. 2010 High-resolution simulation and characterization of density-driven flow in ${\mathrm{CO} }_{2} $ storage in saline aquifers. Adv. Water Resour. 33, 443–455.CrossRefGoogle Scholar
Press, W. H., Flannery, B. P., Teukolsky, S. A. & Vetterling, W. T. 1989 Numerical Recipes (Fortran), 1st edn. Cambridge University Press.Google Scholar
Pritchard, D. 2007 Gravity currents over fractured substrates in a porous medium. J. Fluid Mech. 584, 415–431.CrossRefGoogle Scholar
Riaz, A., Hesse, M. A., Tchelepi, H. A. & Orr, F. M. Jr. 2006 Onset of convection in a gravitationally unstable diffusive layer in porous media. J. Fluid Mech. 548, 87–111.CrossRefGoogle Scholar
Slim, A. C., Bandi, M. M., Miller, J. C. & Mahadevan, L. 2013 Dissolution-driven convection in a Hele-Shaw cell. Phys. Fluids (in press).CrossRefGoogle Scholar
Slim, A. C. & Ramakrishnan, T. S. 2010 Onset and cessation of time-dependent, dissolution-driven convection in porous media. Phys. Fluids 22, 124103.CrossRefGoogle Scholar
Sun, T. & Teja, A. S. 2004 Density, viscosity and thermal conductivity of aqueous solutions of propylene glycol, dipropylene glycol, and tripropylene glycol between 290 K and 460 K. J. Chem. Engng Data 49, 1311–1317.CrossRefGoogle Scholar
Taylor, G. I. 1953 Dipersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
Vella, D., Neufeld, J. A., Huppert, H. E. & Lister, J. R. 2011 Leakage from gravity currents in a porous medium. Part II. A line sink. J. Fluid Mech. 666, 414–427.CrossRefGoogle Scholar
Wang, M.-H., Soriano, A. N., Caparanga, A. R. & Li, M.-H. 2010 Binary mutual diffusion coefficient of aqueous solutions of propylene glycol and dipropylene glycol. J. Taiwan Inst. Chem. Eng. 41, 279–285.CrossRefGoogle Scholar
Wen, B., Dianati, N., Lunasin, E., Chini, G. P. & Doering, C. R. 2012 New upper bounds and reduced dynamical modelling for Rayleigh–Bénard convection in a fluid-saturated porous layer. Commun. Nonlinear Sci. Numer. Simul. 17, 2191–2199.CrossRefGoogle Scholar
Wooding, R. A., Tyler, S. W. & White, I. 1997a Convection in groundwater below an evaporating salt lake: 1. Onset of instability. Water Resour. Res. 33, 1199–1217.CrossRefGoogle Scholar
Wooding, R. A., Tyler, S. W., White, I. & Anderson, P. A. 1997b Convection in groundwater below an evaporating salt lake: 2. Evolution of fingers or plumes. Water Resour. Res. 33, 1219–1228.CrossRefGoogle Scholar
Xu, X., Chen, S. & Zhang, Z. 2006 Convective stability analysis of the long-term storage of carbon dioxide in deep saline aquifers. Adv. Water Resour. 29, 397–497.CrossRefGoogle Scholar