Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T08:40:28.694Z Has data issue: false hasContentIssue false
  • English
  • Français

Convective and absolute instabilities in Rayleigh–Bénard–Poiseuille mixed convection for viscoelastic fluids

Published online by Cambridge University Press:  19 January 2015

S. C. Hirata ,
L. S. de B. Alves ,
N. Delenda  and
M. N. Ouarzazi
S. C. Hirata
Affiliation:
Laboratoire de Mécanique de Lille, UMR CNRS 8107, Université Lille 1, Bld. Paul Langevin, 59655 Villeneuve d’Ascq CEDEX, France
L. S. de B. Alves
Affiliation:
Laboratório de Mecânica Teórica e Aplicada, Departamento de Engenharia Mecânica, Universidade Federal Fluminense, Rua Passo da Pátria 156, Niterói, RJ 24210-240, Brazil
N. Delenda
Affiliation:
Laboratoire de Mécanique de Lille, UMR CNRS 8107, Université Lille 1, Bld. Paul Langevin, 59655 Villeneuve d’Ascq CEDEX, France
M. N. Ouarzazi*
Affiliation:
Laboratoire de Mécanique de Lille, UMR CNRS 8107, Université Lille 1, Bld. Paul Langevin, 59655 Villeneuve d’Ascq CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The convective and absolute nature of instabilities in Rayleigh–Bénard–Poiseuille (RBP) mixed convection for viscoelastic fluids is examined numerically with a shooting method as well as analytically with a one-mode Galerkin expansion. The viscoelastic fluid is modelled by means of a general constitutive equation that encompasses the Maxwell model and the Oldroyd-B model. In comparison to Newtonian fluids, two more dimensionless parameters are introduced, namely the elasticity number 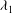${\it\lambda}_{1}$ and the ratio 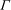${\it\Gamma}$ between retardation and relaxation times. Temporal stability analysis of the basic state showed that the three-dimensional thermoconvective problem can be Squire-transformed. Therefore, one must distinguish mainly between two principal roll orientations: transverse rolls TRs (rolls with axes perpendicular to the Poiseuille flow direction) and longitudinal rolls LRs (rolls with axes parallel to the Poiseuille flow direction). The critical Rayleigh number for the appearance of LRs is found to be independent of the Reynolds number (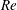$\mathit{Re}$). Depending on 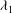${\it\lambda}_{1}$ and 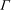${\it\Gamma}$, two different regimes can be distinguished. In the weakly elastic regime, the emerging LRs are stationary, while they are oscillatory in the strongly elastic regime. For TRs, it is found that in the weakly elastic regime, the stabilization effect of 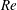$\mathit{Re}$ is more important than in Newtonian fluids. Moreover, for sufficiently elastic fluids a jump is observed in the oscillation frequencies and wavenumbers for moderate 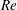$\mathit{Re}$. In the strongly elastic regime, the effect of the imposed throughflow is to promote the appearance of the upstream moving TRs for low values of 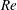$\mathit{Re}$, which are replaced by downstream moving TRs for higher values of 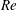$\mathit{Re}$. Moreover, the results proved that, contrary to the case where 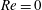$\mathit{Re}=0$, the elasticity number 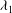${\it\lambda}_{1}$ (the ratio 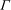${\it\Gamma}$) has a strongly stabilizing (destabilizing) effect when the throughflow is added. The influence of the rheological parameters on the transition curves from convective to absolute instability in the Reynolds–Rayleigh number plane is also determined. We show that the viscoelastic character of the fluid hastens the transition to absolute instability and even may suppress the convective/absolute transition. Throughout this paper, similarities and differences with the corresponding problem for Newtonian fluids are highlighted.

JFM classification

Instability: Absolute/convective instability Convection: Buoyancy-driven instability Non-Newtonian Flows: Viscoelasticity
Type
Papers
Information
Journal of Fluid Mechanics , Volume 765 , 25 February 2015 , pp. 167 - 210
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

de B. Alves, L. S., Kelly, R. E. & Karagozian, A. R. 2008 Transverse jet shear layer instabilities. Part 2. Linear analysis for large jet-to-crossflow velocity ratios. J. Fluid Mech. 602, 383–401.Google Scholar
Bird, R. B., Armstrong, R. C. & Hassager, O. 1987 Dynamics of Polymeric Liquids. John Wiley & Sons.Google Scholar
Brevdo, L. 1991 Three-dimensional absolute and convective instabilities and spatially amplifying waves in parallel shear flows. Z. Angew. Math. Phys. 42 (2), 911–942.Google Scholar
Brevdo, L. 2009 Three-dimensional absolute and convective instabilities at the onset of convection in a porous medium with inclined temperature gradient and vertical throughflow. J. Fluid Mech. 641, 475–487.Google Scholar
Briggs, R. J. 1964 Electron-Stream Interaction with Plasmas. MIT Press.CrossRefGoogle Scholar
Büchel, P. & Lücke, M. 2000a Influence of through-flow on binary fluid convection. Phys. Rev. E 61, 3793.Google ScholarPubMed
Büchel, P. & Lücke, M. 2000b Localized perturbations in binary fluid convection with and without throughflow. Phys. Rev. E 63, 016307.Google Scholar
Carrière, P. & Monkewitz, P. A. 1999 Convective versus absolute instability in mixed Rayleigh–Bénard–Poiseuille convection. J. Fluid Mech. 384, 243–262.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Clarendon.Google Scholar
Coelho, P. M., Pinho, F. T. & Oliveira, P. J. 2002 Fully developed forced convection of the Phan-Thien–Tanner fluid in duts. Intl J. Heat Mass Transfer 45 (7), 1413–1423.Google Scholar
Combarnous, M. & Bories, S. A. 1975 Hydrothermal convection in saturated porous media. Adv. Hydrosci. 10, 231–307.Google Scholar
Delache, A. & Ouarzazi, M. N. 2008 Weakly nonlinear interaction of mixed convection patterns in porous media heated from below. Intl J. Therm. Sci. 47, 709–722.Google Scholar
Delache, A., Ouarzazi, M. N. & Combarnous, M. 2007 Spatio-temporal stability analysis of mixed convection flows in porous media heated from below: comparison with experiments. Intl J. Heat Mass Transfer 50, 1485–1499.Google Scholar
Diaz, E. & Brevdo, L. 2011 Absolute/convective instability dichotomy at the onset of convection in a porous layer with either horizontal or vertical solutal and inclined thermal gradients, and horizontal throughflow. J. Fluid Mech. 681, 567–596.CrossRefGoogle Scholar
Eltayeb, I. A. 1977 Nonlinear thermal convection in an elastiviscous layer heated from below. Proc. R. Soc. Lond. A 356 (1685), 161–176.Google Scholar
Grandjean, E. & Monkewitz, P. A. 2009 Experimental investigation into localized instabilities of mixed Rayleigh–Bénard–Poiseuille convection. J. Fluid Mech. 640, 401–419.CrossRefGoogle Scholar
Green, T. III 1968 Oscillating convection in an elasticoviscous liquid. Phys. Fluids 11 (7), 1410–1412.Google Scholar
Hirata, S. C. & Ouarzazi, M. N. 2010 Three-dimensional absolute and convective instabilities in mixed convection of a viscoelastic fluid through a porous medium. Phys. Lett. A 374 (26), 2661–2666.CrossRefGoogle Scholar
Hu, J., Ben Hadid, H. & Henry, D. 2007 Linear stability analysis of Poiseuille–Rayleigh–Bénard flows in binary fluids with Soret effect. Phys. Fluids 19, 034101.Google Scholar
Hu, J., Yin, X. Y., Henry, D. & Ben Hadid, H. 2009 Spatiotemporal evolution of Poiseuille–Rayleigh–Bénard flows in binary fluids with Soret effect under initial pulselike disturbancies. Phys. Rev. E 80, 026312.Google Scholar
Huerre, P. & Monkewitz, P. A. 1985 Absolute and convective instabilities in free shear layers. J. Fluid Mech. 159, 151–168.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22 (1), 473–537.Google Scholar
Jung, C., Lücke, M. & Büchel, P. 1996 Influence of through-flow on linear pattern formation properties in binary mixture convection. Phys. Rev. E 54, 1510.Google ScholarPubMed
Kelly, R. E. & de B. Alves, L. S. 2008 A uniformly valid asymptotic solution for the transverse jet and its linear stability analysis. Phil. Trans. R. Soc. Lond. A 366, 2729–2744.Google Scholar
Kolka, R. W. & Ierley, G. R. 1987 On the convected linear stability of a viscoelastic Oldroyd-B fluid heated from below. J. Non-Newtonian Fluid Mech. 25, 209–237.Google Scholar
Kolodner, P. 1998 Oscillatory convection in viscoelastic DNA suspensions. J. Non-Newtonian Fluid Mech. 75 (2–3), 167–192.Google Scholar
Kolodner, P., Surko, C. M., Passner, A. & Williams, H. L. 1987 Pulses of oscillatory convection. Phys. Rev. A 36 (5), 2499–2502.CrossRefGoogle ScholarPubMed
Larson, R. G. 1992 Instabilities in viscoelastic flows. Rheol. Acta 31 (3), 213–263.Google Scholar
Li, Z. & Khayat, R. E. 2005 Finite-amplitude Rayleigh–Bénard convection and pattern selection for viscoelastic fluids. J. Fluid Mech. 529, 221–251.Google Scholar
Martinand, D., Carrière, P. & Monkewitz, P. A. 2006 Three-dimensional global instability modes associated with a localized hot spot in Rayleigh–Bénard-Poiseuille convection. J. Fluid Mech. 551, 275–301.Google Scholar
Martinez-Mardones, J. & Perez-Garcia, C. 1990 Linear instability in viscoelastic fluid convection. J. Phys.: Condens. Matter 2 (5), 1281–1290.Google Scholar
Martinez-Mardones, J. & Perez-Garcia, C. 1992 Bifurcation analysis and amplitude equations for viscoelastic convective fluids. Il Nuovo Cimento D 14 (9), 961–975.Google Scholar
Martinez-Mardones, J., Tiemann, R., Walgraef, D. & Zeller, W. 1996 Amplitude equations and pattern selection in viscoelastic convection. Phys. Rev. E 54 (2), 1478–1488.Google Scholar
Mokarizadeh, H., Asgharian, M. & Raisi, A. 2013 Heat transfer in Couette–Poiseuille flow between parallel plates of the Giesekus viscoelastic fluid. J. Non-Newtonian Fluid Mech. 196, 95–101.CrossRefGoogle Scholar
Muller, H. W., Lucke, M. & Kamps, M. 1992 Transversal convection patterns in horizontal shear flow. Phys. Rev. A 45 (6), 3714–3726.Google Scholar
Nicolas, X. 2002 Bibliographical review on the Poiseuille–Rayleigh–Bénard flows: the mixed convection flows in horizontal rectangular ducts heated from below. Intl J. Therm. Sci. 41 (10), 961–1016.CrossRefGoogle Scholar
Nicolas, X., Luijks, J. M. & Platten, J. K. 2000 Linear stability of mixed convection flows in horizontal rectangular channels of finite transversal extension heated from below. Intl J. Heat Mass Transfer 43, 589–610.CrossRefGoogle Scholar
Nicolas, X., Mojtabi, A. & Platten, J. K. 1997 Two-dimensional numerical analysis of the Poiseuille–Bénard flow in a rectangular channel heated from below. Phys. Fluids 9, 337–348.CrossRefGoogle Scholar
Nouar, C., Benaouda-Zouaoui, B. & Desaubry, C. 2000 Laminar mixed convection in a horizontal annular duct. Case of thermodependent non-Newtonian fluid. Eur. J. Mech. (B/Fluids) 19 (3), 423–452.Google Scholar
Ouarzazi, M. N., Mejni, F., Delache, A. & Labrosse, G. 2008 Nonlinear global modes in inhomogeneous mixed convection flows in porous media. J. Fluid Mech. 595, 367–377.CrossRefGoogle Scholar
Ouazzani, M. T., Platten, J. K. & Mojtabi, A. 1990 Experimental study of mixed convection between two horizontal plates at different temperatures – II. Intl J. Heat Mass Transfer 33, 1417–1427.CrossRefGoogle Scholar
Park, H. M. & Lee, H. S. 1996 Hopf bifurcations of viscoelastic fluids heated from below. J. Non-Newtonian Fluid Mech. 66 (1), 1–34.Google Scholar
Peixinho, J., Desaubry, C. & Lebouché, M. 2008 Heat transfer of a non-Newtonian fluid (carbopol aqueous solution) in transitional pipe flow. Intl J. Heat Mass Transfer 51 (1–2), 198–209.Google Scholar
Rosenblat, S. 1986 Thermal convection in a viscoelastic liquid. J. Non-Newtonian Fluid Mech. 21 (2), 201–223.Google Scholar
Sheela-Francisca, J., Tso, C. P., Hung, Y. M. & Rilling, D. 2012 Heat transfer on asymmetric thermal viscous dissipative Couette–Poiseuille flow of pseudo-plastic fluids. J. Non-Newtonian Fluid Mech. 169–170, 42–53.CrossRefGoogle Scholar
Sokolov, M. & Tanner, R. I. 1972 Convective stability of a general viscoelastic fluid heated from below. Phys. Fluids 15 (4), 534–539.Google Scholar
Suslov, S. A. 2006 Numerical aspects of searching convective/absolute instability transition. J. Comput. Phys. 212, 188–217.Google Scholar
Suslov, S. A. & Paolucci, S. 1995 Stability of mixed-convection flow in a tall vertical channel under non-Boussinesq conditions. J. Fluid Mech. 303, 91–115.Google Scholar
Suslov, S. A. & Paolucci, S. 2004 Stability of non-Boussinesq convection via the complex Ginzburg–Landau model. Fluid Dyn. Res. 35, 159–203.Google Scholar
Vest, C. M. & Arpaci, V. S. 1969 Overstability of a viscoelastic fluid layer heated from below. J. Fluid Mech. 36 (3), 613–623.CrossRefGoogle Scholar
Wolfram, S. 2003 The Mathematica Book, 5th edn. Wolfram Media, Cambridge University Press.Google Scholar
Zhang, M., Lashgari, I., Zaki, T. A. & Brandt, L. 2013 Linear stability analysis of channel flow of viscoelastic Oldroyd-B and FENE-P fluids. J. Fluid Mech. 737, 249–279.Google Scholar