Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T14:40:50.204Z Has data issue: false hasContentIssue false
  • English
  • Français

Control of stationary cross-flow modes in a Mach 6 boundary layer using patterned roughness

Published online by Cambridge University Press:  11 October 2018

Thomas Corke Open the ORCID record for Thomas Corke [Opens in a new window] ,
Alexander Arndt ,
Eric Matlis  and
Michael Semper
Thomas Corke*
Affiliation:
University of Notre Dame, Institute for Flow Physics and Control, Aerospace and Mechanical Engineering Department, Notre Dame, IN 46556, USA
Alexander Arndt
Affiliation:
University of Notre Dame, Institute for Flow Physics and Control, Aerospace and Mechanical Engineering Department, Notre Dame, IN 46556, USA
Eric Matlis
Affiliation:
University of Notre Dame, Institute for Flow Physics and Control, Aerospace and Mechanical Engineering Department, Notre Dame, IN 46556, USA
Michael Semper
Affiliation:
U.S. Air Force Academy, Colorado Springs, CO 80840, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

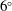Experiments were performed to investigate passive discrete roughness for transition control on a sharp right-circular cone at an angle of attack at Mach 6.0. A cone angle of attack of $6^{\circ }$ was set to produce a mean cross-flow velocity component in the boundary layer over the cone by which the cross-flow instability was the dominant mechanism of turbulent transition. The approach to transition control is based on exciting less-amplified (subcritical) stationary cross-flow modes through the addition of discrete roughness that suppresses the growth of the more-amplified (critical) cross-flow modes, and thereby delays transition. The passive roughness consisted of indentations (dimples) that were evenly spaced around the cone at an axial location that was just upstream of the first linear stability neutral growth branch for cross-flow modes. The experiments were performed in the air force academy (AFA) Mach 6.0 Ludwieg Tube Facility. The cone model was equipped with a motorized three-dimensional traversing mechanism that mounted on the support sting. The traversing mechanism held a closely spaced pair of fast-response total pressure Pitot probes. The measurements consisted of surface oil flow visualization and off-wall azimuthal profiles of mean and fluctuating total pressure at different axial locations. These documented an 25 % increase in the transition Reynolds number with the subcritical roughness. In addition, the experiments revealed evidence of a nonlinear, sum and difference interaction between stationary and travelling cross-flow modes that might indicate a mechanism of early transition in conventional (noisy) hypersonic wind tunnels.

JFM classification

Boundary Layers: Boundary layer control Compressible Flows: Compressible boundary layers Flow Control: Instability control
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 856 , 10 December 2018 , pp. 822 - 849
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bippes, H. 1999 Basic experiments on transition in three-dimensional boundary layers dominated by crossflow instability. Prog. Aerosp. Sci. 35, 363–412.Google Scholar
Bonfigli, G. & Kloker, M. 2007 Secondary instability of crossflow vortices: validation of the stability theory by direct numerical simulation. J. Fluid Mech. 583, 229–272.Google Scholar
Chernoray, V. G., Dovgal, A. V., Kozlov, V. V. & Loefdahl, L. 2005 Experiments on secondary instability of streamwise vortices in a swept-wing boundary layer. J. Fluid Mech. 534, 295–325.Google Scholar
Corke, T. & Knasiak, K. 1998a Stationary-traveling cross-flow mode interactions on a rotating disktransition to turbulence in rotating-disk. J. Fluid Mech. 355, 285–315.Google Scholar
Corke, T. & Matlis, E. 2006 Transition to turbulence in 3-d boundary layers on a rotating disk (triad resonance). In One Hundred Years of Boundary Layer Research, SMIA Book Series, vol. 129. Springer.Google Scholar
Corke, T., Matlis, E. & Othman, H. 2007 Transition to turbulence in rotating-disk boundary layers – convective and absolute instabilities. J. Engng Maths 57, 253–272.Google Scholar
Corke, T. C. & Knasiak, K. F. 1998b Stationary travelling cross-flow mode interactions on a rotating disk. J. Fluid Mech. 355, 285–315.Google Scholar
Craig, S. & Saric, W. 2016 Crossflow instability in a hypersonic boundary layer. J. Fluid Mech. 808, 224–244.Google Scholar
Cummings, R. & McLaughlin, T.2012 Hypersonic Ludwieg tube design and future usage at the U.S. Air Force Academy. In 50th AIAA Aerospace Sciences Meeting. AIAA Paper 2012-0734.Google Scholar
Dörr, P., Kloker, M. & Hanifi, A.2017 Effect of upstream flow deformation using plasma actuators on crossflow transition induced by unsteady vortical free-stream disturbances. In 47th AIAA Fluid Dynamics Conference, AIAA Paper 2017-3114.Google Scholar
Estorf, M., Wolf, T. & Radespiel, R. 2004 Experimental and numerical investigations on the operation of the Hypersonic Ludwieg Tube Braunschweig. In 5th European Symposium on Aerothermodynamics for Space Vehicles.Google Scholar
Glauser, M., Saric, W., Chapman, K. & Reibert, M. 2014 Swept-wing boundary layer transition and turbulent flow physics from multipoint measurements. AIAA J. 52 (2), 338–347.Google Scholar
Juliano, T. & Schneider, S. 2010 Instability and transition on the HIFiRE-5 in a Mach-6 quiet tunnel. In 40th Fluid Dynamics Conference and Exhibit (July), pp. 1–34.Google Scholar
King, R. A. 1992 Three-dimensional boundary-layer transition on a cone at Mach 3.5. Exp. Fluids 13, 305–314.Google Scholar
Li, F., Choudhari, M., Chang, C.-L. & White, J.2010 Analysis of instabilities in non-axisymmetric hypersonic boundary layers over cones. In 10th AIAA/ASME Joint Thermophysics and Heat Transfer Conference, AIAA Paper 2010-4643.Google Scholar
Malik, M., Li, F. & Chang, C.-L. 1994 Crossflow disturbances in three-dimensional boundary layers: nonlinear development, wave interaction and secondary instability. J. Fluid Mech. 268, 1–36.Google Scholar
Malik, M., Li, F., Choudhari, M. & Chang, C.-L. 1999 Secondary instability of crossflow vortices and swept-wing boundary-layer transition. J. Fluid Mech. 399, 85–115.Google Scholar
Morkovin, M. V. 1990a On Roughness-induced Transition: Facts, Views & Speculation, Instability and Transition, vol. I. Springer.Google Scholar
Morkovin, M. V. 1990b Panel Summary on Roughness, Instability and Transition, vol. I. Springer.Google Scholar
Neel, I. T., Leidy, A., Tichenor, N. R. & Bowersox, R. D. 2018 Influence of environmental disturbances on hypersonic crossflow instability on the hifire-5 elliptic cone. In Presented at AIAA Scitech 2018, Paper Number to be Assigned. American Institute of Aeronautics and Astronautics.Google Scholar
Radeztsky, R. H. Jr, Reibert, M. S. & Saric, W. S. 1999 Effect of isolated micron-sized roughness on transition in swept-wing flows. AIAA J. 37 (11), 1370–1377.Google Scholar
Reed, H. L. & Saric, W. S. 1989 Stability of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 21, 235–284.Google Scholar
Reibert, M. S.1996 Nonlinear stability, saturation, and transition in crossflow-dominated boundary layers. PhD thesis, Arizona State University.Google Scholar
Reshotko, E.09–12 June 2008 Paths to Taransition Wall Layers. Papers presented during the AVT-151 RTO AVT/VKI Lecture Series held at the von Karman Institute, Rhode St. Genèse, Belgium.Google Scholar
Saric, W. S. & Reed, H. L.2002 Supersonic laminar flow control on swept wings using distributed roughness. AIAA Paper 2002-0147.Google Scholar
Saric, W. S., Reed, H. L. & Banks, D. W.2004 Flight testing of laminar flow control in high-speed boundary layers. Paper presented at the RTO AVT Specialists’ Meeting on ‘Enhancement of NATO Military Flight Vehicle Performance by Managemenet of Interacting Boundary Layer Transition and Separation’, held in Prague, Czech Republic 4–7 October 2004, Published in RTO-MP-AVT-111.Google Scholar
Saric, W. S., Reed, H. L. & Kerschen, E. J. 2002 Boundary-layer receptivity to freestream disturbances. Annu. Rev. Fluid Mech. 34, 291–319.Google Scholar
Saric, W. S., Reed, H. L. & White, E. B. 2003 Stability and transition of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 35, 413–440.Google Scholar
Saric, W. S., Ruben, C. C. & Reibert, M. S.1998 Leading-edge roughness as a transition control mechanism. AIAA Paper AIAA-98-0781.Google Scholar
Schuele, C.-Y.2011 Control of stationary cross-flow modes in a Mach 3.5 boundary layer using passive and active roughness. PhD thesis, University of Notre Dame, Notre Dame, IN.Google Scholar
Schuele, C.-Y., Corke, T. & Matlis, E. 2013 Control of stationary cross-flow modes in a Mach 3.5 boundary layer using patterned passive and active roughness. J. Fluid Mech. 718, 5–38.Google Scholar
Semionov, N. V. & Kosinov, A. D. 2007 Method laminar-turbulent transition control of supersonic boundary layer on a swept wing. Thermophys. Aeromech. 14 (3), 337–341.Google Scholar
Semionov, N. V., Kosinov, A. D. & Levchenko, V. Ya. 2006 Experimental study of turbulence beginning and transition control in a supersonic boundary layer on swept wing. In Sixth IUTAM Symposium on Laminar Turbulent Transition (ed. Govindarajan, R.).Google Scholar
Swanson, E. & Schneider, S.2010 Boundary-layer transition on cones at angle of attack in a Mach-6 quiet tunnel. In 48th AIAA Aerosciences Meeting. Paper AIAA 2010-1062.Google Scholar
Wassermann, P. & Kloker, M. 2002 Mechanisms and passive control of crossflow-vortex-induced transition in three-dimensional boundary layer. J. Fluid Mech. 456, 49–84.Google Scholar
White, E. B. & Saric, W. S. 2005 Secondary instability of crossflow vortices. J. Fluid Mech. 525, 275–308.Google Scholar
Wolf, S. W. D. & Laub, J. A.1997 NASA Ames Laminar Flow Supersonic WInd Tunnel (LFSWT) Tests of a $10^{\circ }$ Cone at Mach 1.6. NASA-TM 110438.Google Scholar