Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Niegodajew, Paweł
Dróżdż, Artur
and
Elsner, Witold
2019.
A new approach for estimation of the skin friction in turbulent boundary layer under the adverse pressure gradient conditions.
International Journal of Heat and Fluid Flow,
Vol. 79,
Issue. ,
p.
108456.
Hwang, Jinyul
Lee, Jae Hwa
and
Sung, Hyung Jin
2020.
Statistical behaviour of self-similar structures in canonical wall turbulence.
Journal of Fluid Mechanics,
Vol. 905,
Issue. ,
Mäteling, Esther
Klaas, Michael
and
Schröder, Wolfgang
2020.
Simultaneous Stereo PIV and MPS3 Wall-Shear Stress Measurements in Turbulent Channel Flow.
Optics,
Vol. 1,
Issue. 1,
p.
40.
Cheng, Cheng
Li, Weipeng
Lozano-Durán, Adrián
and
Liu, Hong
2020.
On the structure of streamwise wall-shear stress fluctuations in turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
Cheng, Cheng
Li, Weipeng
Lozano-Durán, Adrián
Fan, Yitong
and
Liu, Hong
2020.
On the structure of streamwise wall-shear stress fluctuations in turbulent channel flows.
Journal of Physics: Conference Series,
Vol. 1522,
Issue. 1,
p.
012010.
Lozano-Durán, Adrián
Bae, H. Jane
and
Encinar, Miguel P.
2020.
Causality of energy-containing eddies in wall turbulence.
Journal of Fluid Mechanics,
Vol. 882,
Issue. ,
Leschziner, Michael A.
2020.
Friction-Drag Reduction by Transverse Wall Motion – A Review.
Journal of Mechanics,
Vol. 36,
Issue. 5,
p.
649.
Cheng, Cheng
Li, Weipeng
Lozano-Durán, Adrián
and
Liu, Hong
2020.
Uncovering Townsend’s wall-attached eddies in low-Reynolds-number wall turbulence.
Journal of Fluid Mechanics,
Vol. 889,
Issue. ,
Zhao, Ming-Xiang
Yu, Ming
and
Cao, Tao
2021.
Drag reduction in turbulent Taylor–Couette flow by axial oscillation of inner cylinder.
Physics of Fluids,
Vol. 33,
Issue. 5,
Duan, Yanchong
Zhong, Qiang
Wang, Guiquan
Zhang, Peng
and
Li, Danxun
2021.
Contributions of different scales of turbulent motions to the mean wall-shear stress in open channel flows at low-to-moderate Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 918,
Issue. ,
Chernyshenko, Sergei
2021.
Extension of QSQH theory of scale interaction in near-wall turbulence to all velocity components.
Journal of Fluid Mechanics,
Vol. 916,
Issue. ,
Dróżdż, Artur
Niegodajew, Paweł
Romańczyk, Mathias
and
Elsner, Witold
2021.
Effect of Reynolds number on turbulent boundary layer approaching separation.
Experimental Thermal and Fluid Science,
Vol. 125,
Issue. ,
p.
110377.
Agostini, Lionel
and
Leschziner, Michael
2021.
Statistical analysis of outer large-scale/inner-layer interactions in channel flow subjected to oscillatory drag-reducing wall motion using a multiple-variable joint-probability-density function methodology.
Journal of Fluid Mechanics,
Vol. 923,
Issue. ,
Dróżdż, Artur
Niegodajew, Paweł
Romańczyk, Mathias
Sokolenko, Vasyl
and
Elsner, Witold
2021.
Effective use of the streamwise waviness in the control of turbulent separation.
Experimental Thermal and Fluid Science,
Vol. 121,
Issue. ,
p.
110291.
Bae, H. Jane
Lozano-Durán, A.
and
McKeon, Beverley J.
2021.
Nonlinear mechanism of the self-sustaining process in the buffer and logarithmic layer of wall-bounded flows.
Journal of Fluid Mechanics,
Vol. 914,
Issue. ,
Zhang, Qing-fu
Pan, Chong
and
Wang, Jin-jun
2022.
De-asymmetry of small-scale motions in wall-bounded turbulence.
Physics of Fluids,
Vol. 34,
Issue. 6,
Zheng, Xiaobo
Bellani, Gabriele
Mascotelli, Lucia
Örlü, Ramis
Ianiro, Andrea
Vila, Carlos Sanmiguel
Discetti, Stefano
Serpieri, Jacopo
Raiola, Marco
Talamelli, Alessandro
Li, Ye
and
Jiang, Nan
2022.
Inter-scale interaction in pipe flows at high Reynolds numbers.
Experimental Thermal and Fluid Science,
Vol. 131,
Issue. ,
p.
110529.
Fan, Yitong
Atzori, Marco
Vinuesa, Ricardo
Gatti, Davide
Schlatter, Philipp
and
Li, Weipeng
2022.
Decomposition of the mean friction drag on an NACA4412 airfoil under uniform blowing/suction.
Journal of Fluid Mechanics,
Vol. 932,
Issue. ,
Agostini, L.
and
Leschziner, M.
2022.
Auto-encoder-assisted analysis of amplitude and wavelength modulation of near-wall turbulence by outer large-scale structures in channel flow at friction Reynolds number of 5200.
Physics of Fluids,
Vol. 34,
Issue. 11,
Cheng, Cheng
and
Fu, Lin
2022.
Large-scale motions and self-similar structures in compressible turbulent channel flows.
Physical Review Fluids,
Vol. 7,
Issue. 11,
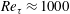 $Re_{\unicode[STIX]{x1D70F}}\approx 1000$
$Re_{\unicode[STIX]{x1D70F}}\approx 1000$