Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-04T21:39:36.949Z Has data issue: false hasContentIssue false
  • English
  • Français

Concentration banding instability of a sheared bacterial suspension

Published online by Cambridge University Press:  06 October 2020

Laxminarsimharao Vennamneni Open the ORCID record for Laxminarsimharao Vennamneni [Opens in a new window] ,
Piyush Garg Open the ORCID record for Piyush Garg [Opens in a new window]  and
Ganesh Subramanian Open the ORCID record for Ganesh Subramanian [Opens in a new window]
Laxminarsimharao Vennamneni
Affiliation:
Engineering Mechanics Unit, JNCASR, Jakkur, Bangalore 560064, India
Piyush Garg
Affiliation:
Engineering Mechanics Unit, JNCASR, Jakkur, Bangalore 560064, India
Ganesh Subramanian*
Affiliation:
Engineering Mechanics Unit, JNCASR, Jakkur, Bangalore 560064, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

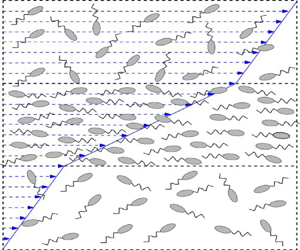
We demonstrate a novel shear-induced mechanism for growth of concentration fluctuations in a bacterial suspension. Using a linear stability analysis, a homogeneous bacterial suspension, subject to a simple shear flow, is shown to be susceptible to exponentially growing layering perturbations in the shear rate and bacterial concentration. A semi-analytical expression for the growth rate of concentration perturbations is first obtained using the method of multiple scales, in the limit where the time scales characterizing the positional and orientation degrees of freedom are well separated. Next, the eigenspectrum obtained numerically from a full linear stability analysis is used to validate and extend the multiple scales result, and draw a contrast with the known orientation-shear instability. Finally, fully nonlinear simulations, but restricted to one-dimensional variations of the relevant fields (velocity, concentration and swimmer orientation distribution) show that the initial instability leads to gradient-banded velocity profiles, with a local depletion of bacteria at the interface between the homogeneous shear bands. Our results demonstrate that long-ranged hydrodynamic interactions serve as an alternate explanation for recent observations of shear bands in bacterial suspensions.

JFM classification

Biological Fluid Dynamics: Micro-organism dynamics Non-Newtonian Flows: Rheology
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 904 , 10 December 2020 , A7
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Arfken, G. B. & Weber, H. J. 1999 Mathematical Methods for Physicists. Academic Press.Google Scholar
Barry, M. T., Rusconi, R., Guasto, J. S. & Stocker, R. 2015 Shear-induced orientational dynamics and spatial heterogeneity in suspensions of motile phytoplankton. J. R. Soc. Interface 12 (112), 20150791.CrossRefGoogle ScholarPubMed
Batchelor, G. K. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41 (3), 545–570.CrossRefGoogle Scholar
Bearon, R. N. & Hazel, A. L. 2015 The trapping in high-shear regions of slender bacteria undergoing chemotaxis in a channel. J. Fluid Mech. 771, R3.CrossRefGoogle Scholar
Bechtel, T. M. & Khair, A. S. 2017 Linear viscoelasticity of a dilute active suspension. Rheol. Acta 56 (2), 149–160.CrossRefGoogle Scholar
Berke, A. P., Turner, L., Berg, H. C. & Lauga, E. 2008 Hydrodynamic attraction of swimming microorganisms by surfaces. Phys. Rev. Lett. 101 (3), 038102.CrossRefGoogle ScholarPubMed
Boyd, J. P. 2001 Chebyshev and Fourier Spectral Methods. Courier Corporation.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Thomas, A. Jr 2012 Spectral Methods in Fluid Dynamics. Springer Science and Business Media.Google Scholar
Cates, M. E. & Fielding, S. M. 2006 Rheology of giant micelles. Adv. Phys. 55 (7–8), 799–879.CrossRefGoogle Scholar
Cates, M. E., Fielding, S. M., Marenduzzo, D., Orlandini, E. & Yeomans, J. M. 2008 Shearing active gels close to the isotropic-nematic transition. Phys. Rev. Lett. 101 (6), 068102.CrossRefGoogle ScholarPubMed
Clement, E., Lindner, A., Douarche, C. & Auradou, H. 2016 Bacterial suspensions under flow. Eur. Phys. J. 225 (11–12), 2389–2406.Google Scholar
Cromer, M., Fredrickson, G. H. & Leal, L. G. 2014 A study of shear banding in polymer solutions. Phys. Fluids 26 (6), 063101.CrossRefGoogle Scholar
Cromer, M., Villet, M. C., Fredrickson, G. H. & Leal, L. G. 2013 Shear banding in polymer solutions. Phys. Fluids 25 (5), 051703.CrossRefGoogle Scholar
De Gennes, P.-G. & Prost, J. 1993 The Physics of Liquid Crystals, vol. 83. Oxford University Press.Google Scholar
Dhont, J. K. G. & Briels, W. J. 2008 Gradient and vorticity banding. Rheol. Acta 47 (3), 257–281.CrossRefGoogle Scholar
Divoux, T., Fardin, M. A., Manneville, S. & Lerouge, S. 2016 Shear banding of complex fluids. Annu. Rev. Fluid Mech. 48, 81–103.CrossRefGoogle Scholar
Dixon, P. K., Pine, D. J. & Wu, X.-L. 1992 Mode selection in the dynamics of sheared polymer solutions. Phys. Rev. Lett. 68 (14), 2239.CrossRefGoogle ScholarPubMed
Doi, M. & Edwards, S. F. 1978 Dynamics of rod-like macromolecules in concentrated solution. Part 2. J. Chem. Soc. Faraday Trans. 74, 918–932.CrossRefGoogle Scholar
Dombrowski, C., Cisneros, L., Chatkaew, S., Goldstein, R. E. & Kessler, J. O. 2004 Self-concentration and large-scale coherence in bacterial dynamics. Phys. Rev. Lett. 93 (9), 098103.CrossRefGoogle ScholarPubMed
Doostmohammadi, A., Ignés-Mullol, J., Yeomans, J. M. & Sagués, F. 2018 Active nematics. Nat. Commun. 9 (1), 1–13.CrossRefGoogle ScholarPubMed
Drescher, K., Dunkel, J., Cisneros, L. H., Ganguly, S. & Goldstein, R. E. 2011 Fluid dynamics and noise in bacterial cell–cell and cell–surface scattering. Proc. Natl Acad. Sci. USA 108 (27), 10940–10945.CrossRefGoogle ScholarPubMed
Dunkel, J., Heidenreich, S., Drescher, K., Wensink, H. H., Bär, M. & Goldstein, R. E. 2013 Fluid dynamics of bacterial turbulence. Phys. Rev. Lett. 110 (22), 228102.CrossRefGoogle ScholarPubMed
Elgeti, J. & Gompper, G. 2016 Microswimmers near surfaces. Eur. Phys. J. 225 (11–12), 2333–2352.Google Scholar
Ezhilan, B. & Saintillan, D. 2015 Transport of a dilute active suspension in pressure-driven channel flow. J. Fluid Mech. 777, 482–522.CrossRefGoogle Scholar
Fielding, S. M. 2005 Linear instability of planar shear banded flow. Phys. Rev. Lett. 95 (13), 134501.CrossRefGoogle ScholarPubMed
Fielding, S. M., Marenduzzo, D. & Cates, M. E. 2011 Nonlinear dynamics and rheology of active fluids: simulations in two dimensions. Phys. Rev. E 83 (4), 041910.CrossRefGoogle ScholarPubMed
Fielding, S. M. & Olmsted, P. D. 2003 Flow phase diagrams for concentration-coupled shear banding. Eur. Phys. J. E 11 (1), 65–83.CrossRefGoogle ScholarPubMed
Gachelin, J., Mino, G., Berthet, H., Lindner, A., Rousselet, A. & Clément, É. 2013 Non-newtonian viscosity of escherichia coli suspensions. Phys. Rev. Lett. 110 (26), 268103.CrossRefGoogle ScholarPubMed
Gachelin, J., Rousselet, A., Lindner, A. & Clement, E. 2014 Collective motion in an active suspension of escherichia coli bacteria. New. J. Phys. 16 (2), 025003.CrossRefGoogle Scholar
Giomi, L., Liverpool, T. B. & Marchetti, M. C. 2010 Sheared active fluids: thickening, thinning, and vanishing viscosity. Phys. Rev. E 81 (5), 051908.CrossRefGoogle ScholarPubMed
Giomi, L., Marchetti, M. C. & Liverpool, T. B. 2008 Complex spontaneous flows and concentration banding in active polar films. Phys. Rev. Lett. 101 (19), 198101.CrossRefGoogle ScholarPubMed
Guo, S., Samanta, D., Peng, Y., Xu, X. & Cheng, X. 2018 Symmetric shear banding and swarming vortices in bacterial superfluids. Proc. Natl Acad. Sci. 115 (28), 7212–7217.CrossRefGoogle ScholarPubMed
Hatwalne, Y., Ramaswamy, S., Rao, M. & Simha, R. A. 2004 Rheology of active-particle suspensions. Phys. Rev. Lett. 92 (11), 118101.CrossRefGoogle ScholarPubMed
Helfand, E. & Fredrickson, G. H. 1989 Large fluctuations in polymer solutions under shear. Phys. Rev. Lett. 62 (21), 2468.CrossRefGoogle ScholarPubMed
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161.Google Scholar
Kasyap, T. V. & Koch, D. L. 2012 Chemotaxis driven instability of a confined bacterial suspension. Phys. Rev. Lett. 108 (3), 038101.CrossRefGoogle ScholarPubMed
Kasyap, T. V. & Koch, D. L. 2014 Instability of an inhomogeneous bacterial suspension subjected to a chemo-attractant gradient. J. Fluid Mech. 741, 619–657.CrossRefGoogle Scholar
Kasyap, T. V., Koch, D. L. & Wu, M. 2014 Bacterial collective motion near the contact line of an evaporating sessile drop. Phys. Fluids 26 (11), 111703.CrossRefGoogle Scholar
Koch, D. L. & Subramanian, G. 2011 Collective hydrodynamics of swimming microorganisms: living fluids. Annu. Rev. Fluid Mech. 43, 637–659.CrossRefGoogle Scholar
Krishnamurthy, D. & Subramanian, G. 2015 Collective motion in a suspension of micro-swimmers that run-and-tumble and rotary diffuse. J. Fluid Mech. 781, 422–466.CrossRefGoogle Scholar
Larson, R. G. 1992 Flow-induced mixing, demixing, and phase transitions in polymeric fluids. Rheol. Acta 31 (6), 497–520.CrossRefGoogle Scholar
Larson, R. G. 2013 Constitutive Equations for Polymer Melts and Solutions: Butterworths Series in Chemical Engineering. Butterworth-Heinemann.Google Scholar
Li, H., Shi, X.-Q., Huang, M., Chen, X., Xiao, M., Liu, C., Chaté, H. & Zhang, H. P. 2019 Data-driven quantitative modeling of bacterial active nematics. Proc. Natl Acad. Sci. 116 (3), 777–785.CrossRefGoogle ScholarPubMed
Loisy, A., Eggers, J. & Liverpool, T. B. 2018 Active suspensions have nonmonotonic flow curves and multiple mechanical equilibria. Phys. Rev. Lett. 121, 018001.CrossRefGoogle ScholarPubMed
López, H. M., Gachelin, J., Douarche, C., Auradou, H. & Clément, E. 2015 Turning bacteria suspensions into superfluids. Phys. Rev. Lett. 115, 028301.CrossRefGoogle ScholarPubMed
Mackaplow, M. B. & Shaqfeh, E. S. G. 1998 A numerical study of the sedimentation of fibre suspensions. J. Fluid Mech. 376, 149–182.CrossRefGoogle Scholar
Marchetti, M. C., Joanny, J. -F., Ramaswamy, S., Liverpool, T. B., Prost, J., Rao, M. & Simha, R. A. 2013 Hydrodynamics of soft active matter. Rev. Mod. Phys. 85 (3), 1143.CrossRefGoogle Scholar
Martinez, V. A., Clément, E., Arlt, J., Douarche, C., Dawson, A., Schwarz-Linek, J., Creppy, A. K., Škultéty, V., Morozov, A. N.Auradou, H. et al. 2020 A combined rheometry and imaging study of viscosity reduction in bacterial suspensions. Proc. Natl Acad. Sci. 117 (5), 2326–2331.CrossRefGoogle ScholarPubMed
Messiah, A. 1962 Quantum Mechanics, vol. 2. North-Holland.Google Scholar
Miles, C. J., Evans, A. A., Shelley, M. J. & Spagnolie, S. E. 2019 Active matter invasion of a viscous fluid: unstable sheets and a no-flow theorem. Phys. Rev. Lett. 122 (9), 098002.CrossRefGoogle Scholar
Milner, S. T. 1993 Dynamical theory of concentration fluctuations in polymer solutions under shear. Phys. Rev. E 48 (5), 3674.CrossRefGoogle ScholarPubMed
Nambiar, S., Garg, P. & Subramanian, G. 2019 a Enhanced velocity fluctuations in interacting swimmer suspensions. arXiv:1902.05304.Google Scholar
Nambiar, S., Nott, P. R. & Subramanian, G. 2017 Stress relaxation in a dilute bacterial suspension. J. Fluid Mech. 812, 41–64.CrossRefGoogle Scholar
Nambiar, S., Phanikanth, S., Nott, P. R. & Subramanian, G. 2019 b Stress relaxation in a dilute bacterial suspension: the active–passive transition. J. Fluid Mech. 870, 1072–1104.CrossRefGoogle Scholar
Nitsche, L. C. & Hinch, E. J. 1997 Shear-induced lateral migration of brownian rigid rods in parabolic channel flow. J. Fluid Mech. 332, 1–21.CrossRefGoogle Scholar
Olmsted, P. D. 2008 Perspectives on shear banding in complex fluids. Rheol. Acta 47 (3), 283–300.CrossRefGoogle Scholar
Onuki, A. 2002 Phase Transition Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Pahlavan, A. A. & Saintillan, D. 2011 Instability regimes in flowing suspensions of swimming micro-organisms. Phys. Fluids 23 (1), 011901.CrossRefGoogle Scholar
Rusconi, R., Guasto, J. S. & Stocker, R. 2014 Bacterial transport suppressed by fluid shear. Nat. Phys. 10 (3), 212.CrossRefGoogle Scholar
Saintillan, D. 2010 The dilute rheology of swimming suspensions: a simple kinetic model. Exp. Mech. 50 (9), 1275–1281.CrossRefGoogle Scholar
Saintillan, D. 2018 Rheology of active fluids. Annu. Rev. Fluid Mech. 50, 563–592.CrossRefGoogle Scholar
Saintillan, D. & Shelley, M. J. 2007 Orientational order and instabilities in suspensions of self-locomoting rods. Phys. Rev. Lett. 99 (5), 058102.CrossRefGoogle ScholarPubMed
Saintillan, D. & Shelley, M. J. 2008 a Instabilities and pattern formation in active particle suspensions: kinetic theory and continuum simulations. Phys. Rev. Lett. 100 (17), 178103.CrossRefGoogle ScholarPubMed
Saintillan, D. & Shelley, M. J. 2008 b Instabilities, pattern formation, and mixing in active suspensions. Phys. Fluids 20 (12), 123304.CrossRefGoogle Scholar
Sanchez, T., Chen, D. T. N., DeCamp, S. J., Heymann, M. & Dogic, Z. 2012 Spontaneous motion in hierarchically assembled active matter. Nature 491 (7424), 431–434.CrossRefGoogle ScholarPubMed
Schwarz-Linek, J., Arlt, J., Jepson, A., Dawson, A., Vissers, T., Miroli, D., Pilizota, T., Martinez, V. A. & Poon, W. C. K. 2016 Escherichia coli as a model active colloid: a practical introduction. Colloids Surf. B 137, 2–16.CrossRefGoogle ScholarPubMed
Secchi, E., Rusconi, R., Buzzaccaro, S., Salek, M. M., Smriga, S., Piazza, R. & Stocker, R. 2016 Intermittent turbulence in flowing bacterial suspensions. J. R. Soc. Interface 13 (119), 20160175.CrossRefGoogle ScholarPubMed
Simha, R. A. & Ramaswamy, S. 2002 Hydrodynamic fluctuations and instabilities in ordered suspensions of self-propelled particles. Phys. Rev. Lett. 89 (5), 058101.CrossRefGoogle Scholar
Sokolov, A. & Aranson, I. S. 2009 Reduction of viscosity in suspension of swimming bacteria. Phys. Rev. Lett. 103 (14), 148101.CrossRefGoogle ScholarPubMed
Sokolov, A. & Aranson, I. S. 2012 Physical properties of collective motion in suspensions of bacteria. Phys. Rev. Lett. 109 (24), 248109.CrossRefGoogle Scholar
Sokolov, A. & Aranson, I. S. 2016 Rapid expulsion of microswimmers by a vortical flow. Nat. Commun. 7, 11114.CrossRefGoogle ScholarPubMed
Sokolov, A., Aranson, I. S., Kessler, J. O. & Goldstein, R. E. 2007 Concentration dependence of the collective dynamics of swimming bacteria. Phys. Rev. Lett. 98 (15), 158102.CrossRefGoogle ScholarPubMed
Stenhammar, J., Nardini, C., Nash, R. W., Marenduzzo, D. & Morozov, A. 2017 Role of correlations in the collective behavior of microswimmer suspensions. Phys. Rev. Lett. 119 (2), 028005.CrossRefGoogle ScholarPubMed
Subramanian, G. & Brady, J. F. 2004 Multiple scales analysis of the Fokker–Planck equation for simple shear flow. Physica A 334 (3–4), 343–384.CrossRefGoogle Scholar
Subramanian, G. & Koch, D. L. 2009 Critical bacterial concentration for the onset of collective swimming. J. Fluid Mech. 632, 359–400.CrossRefGoogle Scholar
Underhill, P. T., Hernandez-Ortiz, J. P. & Graham, M. D. 2008 Diffusion and spatial correlations in suspensions of swimming particles. Phys. Rev. Lett. 100 (24), 248101.CrossRefGoogle ScholarPubMed
Vennamneni, L., Nambiar, S. & Subramanian, G. 2020 Shear-induced migration of microswimmers in pressure-driven channel flow. J. Fluid Mech. 890, A15.CrossRefGoogle Scholar
Wensink, H. H., Dunkel, J., Heidenreich, S., Drescher, K., Goldstein, R. E., Löwen, H. & Yeomans, J. M. 2012 Meso-scale turbulence in living fluids. Proc. Natl Acad. Sci. USA 109 (36), 14308–14313.CrossRefGoogle ScholarPubMed
Wu, X.-L. & Libchaber, A. 2000 Particle diffusion in a quasi-two-dimensional bacterial bath. Phys. Rev. Lett. 84 (13), 3017.CrossRefGoogle Scholar
Wu, X.-L., Pine, D. J. & Dixon, P. K. 1991 Enhanced concentration fluctuations in polymer solutions under shear flow. Phys. Rev. Lett. 66 (18), 2408.CrossRefGoogle ScholarPubMed