Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-18T03:19:52.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Computational study of the interaction of freely moving particles at intermediate Reynolds numbers

Published online by Cambridge University Press:  06 July 2012

Açmae El Yacoubi ,
Sheng Xu  and
Z. Jane Wang
Açmae El Yacoubi
Affiliation:
Department of Mechanical & Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA
Sheng Xu
Affiliation:
Department of Mathematics, Southern Methodist University, Dallas, TX 75275-0156, USA
Z. Jane Wang*
Affiliation:
Department of Mechanical & Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA Department of Physics, Cornell University, Ithaca, NY 14853, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by our interest in understanding collective behaviour and self-organization resulting from hydrodynamic interactions, we investigate the two-dimensional dynamics of horizontal arrays of settling cylinders at intermediate Reynolds numbers. To simulate these dynamics, we develop a direct numerical simulation based on the immersed interface method. A novel aspect of our method is its ability to efficiently and accurately couple the dynamics of the freely moving objects with the fluid. We report the falling configuration and the wake pattern of the array, and investigate their dependence on the number of particles, , as well as the initial inter-particle spacing, 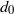. We find that, in the case of odd-numbered arrays, the middle cylinder is always leading, whereas in the case of even-numbered arrays, the steady-state shape is concave-down. In large arrays 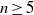, the outer pairs tend to cluster. In addition, we analyse detailed kinematics, wakes and forces of three settling cylinders. We find that the middle one experiences a higher drag force in the presence of neighbouring cylinders, compared to an isolated settling cylinder, resulting in a decrease in its settling velocity. For a small initial spacing 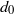, the middle cylinder experiences a strong sideway repulsive force, the magnitude of which increases with decreasing 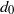. During the fall, the left and right cylinders rotate outwards and shed vortices in anti-phase.

JFM classification

Mathematical Foundations: Computational methods Multiphase and Particle-laden Flows: Particle/fluid flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 705: Special issue dedicated to Professor T. J. Pedley on his 70th birthday , 25 August 2012 , pp. 134 - 148
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Andersen, A., Pesavento, U. & Wang, Z. J. 2005a Unsteady aerodynamics of fluttering and tumbling plates. J. Fluid Mech. 541, 65–90.CrossRefGoogle Scholar
2. Andersen, A., Pesavento, U. & Wang, Z. J. 2005b Analysis of transitions between fluttering, tumbling and steady descent of falling cards. J. Fluid Mech. 541, 91–104.CrossRefGoogle Scholar
3. Ardekani, A. M., Dabiri, S. & Rangel, R. H. 2008 Collision of multi-particle and general shape objects in a viscous fluid. J. Comput. Phys. 227, 10094–10107.CrossRefGoogle Scholar
4. Ardekani, A. M. & Rangel, R. H. 2006 Unsteady motion of two solid spheres in Stokes flow. Phys. Fluids 18, 103306.Google Scholar
5. Bearman, P. W. & Wadock, A. J. 1973 The interaction between a pair of circular cylinders normal to a stream. J. Fluid Mech. 61, 499–511.Google Scholar
6. Cisneros, L. H., Cortez, R., Dombrowski, C., Goldstein, R. E. & Kessler, J. O. 2007 Fluid dynamics of self-propelled microorganisms, from individuals to concentrated populations. Exp. Fluids 43, 737–753.CrossRefGoogle Scholar
7. Couzin, I. D. & Krause, J. 2003 Self-organization and collective behaviour in vertebrates. J. Adv. Study Behav. 32, 1–75.Google Scholar
8. Crowley, J. M. 1971 Viscosity induced instability of a one-dimensional lattice of falling spheres. J. Fluid Mech. 45, 151–159.Google Scholar
9. Czirók, A. & Vicsek, T. 2006 Collective behaviour of interacting self-propelled particles. Physica A 281, 17–29.Google Scholar
10. Daniel, W. B., Ecke, R. E., Subramanian, G. & Koch, D. 2009 Clusters of sedimenting high-Reynolds-number particles. J. Fluid Mech. 625, 371–385.Google Scholar
11. Darnton, N. C., Turner, L., Rojevsky, S. & Berg, H. C. 2010 Dynamics of bacterial swarming. Biophys. J. 98 (10), 2082–2090.CrossRefGoogle ScholarPubMed
12. Ekiel-Jeżewska, M. L., Metzger, B. & Guazzelli, É. 2006 Spherical cloud of point particles falling in a viscous fluid. Phys. Fluids 18, 038104.Google Scholar
13. Fortes, A. F., Joseph, D. D. & Lundgren, T. S. 1987 Nonlinear mechanics of fluidization of beds of spherical particles. J. Fluid Mech. 177, 467–483.CrossRefGoogle Scholar
14. Gregor, T., Fujimoto, K., Masaki, N. & Sawai, S. 2010 The onset of collective behaviour in social amoebae. Science 328 (5981), 1021–1025.CrossRefGoogle Scholar
15. Guazzelli, É. & Hinch, J. 2011 Fluctuations and instability in sedimentation. Annu. Rev. Fluid Mech. 43, 97–116.Google Scholar
16. Happel, J. & Brenner, H. 1973 Low Reynolds number hydrodynamics: with special applications to particulate media. In Mechanics of Fluids and Transport Processes. Springer.Google Scholar
17. Happel, J. & Pfeffer, R. 1960 The motion of two spheres following each other in a viscous fluid. AIChE J. 6, 129.Google Scholar
18. Hernandez-Ortiz, J. P., Stoltz, C. G. & Graham, M. D. 2005 Transport and collective dynamics in suspensions of confined swimming particles. Phys. Rev. Lett. 95, 204501.Google Scholar
19. Hill, R. J., Koch, D. L. & Ladd, A. J. C. 2001 The first effects of fluid inertia on flows in ordered and random arrays of spheres. J. Fluid Mech. 448, 213–241.CrossRefGoogle Scholar
20. Hocking, L. M. 1963 The behaviour of clusters of spheres falling in a viscous fluid. Part 2. Slow motion theory. J. Fluid Mech. 20, 129–139.Google Scholar
21. Jayaweera, K. O. L. F. & Mason, B. J. 1963 The behaviour of clusters of spheres falling in a viscous fluid. Part 1. Experiment. J. Fluid Mech. 20, 121–128.CrossRefGoogle Scholar
22. Jayaweera, K. O. L. F. & Mason, B. J. 1965 The behaviour of freely falling cylinders and cones in a viscous fluid. J. Fluid Mech. 22, 709–720.Google Scholar
23. Jenny, M., Dušek, J. & Bouchet, G. 2004 Instabilities and transition of a sphere falling or ascending freely in a Newtonian fluid. J. Fluid Mech. 508, 201–239.Google Scholar
24. Kaiser, D. 2007 Bacterial swarming: a re-examination of cell-movement patterns. Curr. Biol. 17, 561–570.Google Scholar
25. Kang, S. 2003 Characteristics of flow over two circular cylinders in a side-by-side arrangement at low Reynolds numbers. Phys. Fluids 15, 9.Google Scholar
26. Katija, K. & Dabiri, J. O. 2009 A viscosity-enhanced mechanism for biogenic ocean mixing. Nature 460, 624–626.Google Scholar
27. Kim, I., Elghobashi, S. & Sirignano, W. 2005 Three-dimensional flow over two spheres placed side by side. J. Fluid Mech. 246, 465.Google Scholar
28. Kim, M. & Breuer, K. S. 2004 Enhanced diffusion due to motile bacteria. Phys. Fluids 16, L78.Google Scholar
29. Koch, D. L. & Subramanian, G. 2011 Collective hydrodynamics of swimming microorganisms: living fluids. Annu. Rev. Fluid Mech. 43, 637–659.Google Scholar
30. Legendre, D., Magnaudet, J. & Mougin, G. 2003 Hydrodynamic interactions between two spherical bubbles rising side by side in a viscous fluid. J. Fluid Mech. 497, 133–166.Google Scholar
31. Leichtberg, S., Weinbaum, S., Pfeffer, R. & Gluckman, J. 1976 A study of unsteady forces at low Reynolds number: a strong interaction theory for the coaxial settling of three or more spheres. Phil. Trans. R. Soc. Lond. A 282 (1311), 585–610.Google Scholar
32. LeVeque, R. J. & Li, Z. 1994 The immersed interface method for elliptic equations with discontinuous coefficients and singular sources. SIAM J. Numer. Anal. 31 (4), 1019–1044.Google Scholar
33. Li, Z., Wan, X., Ito, K. & Lubkin, S. R. 2006 An augmented approach for the pressure boundary condition in a Stokes flow. Commun. Comput. Phys. 1, 874–885.Google Scholar
34. Meneghini, J. R., Saltara, F., Siquiera, C. L. R. & Ferrari, J. A. Jr 2000 Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements. J. Fluids Struct. 15, 327–350.Google Scholar
35. Metzger, B., Nicolas, M. & Guazzelli, É. 2007 Falling clouds of particles in viscous fluids. J. Fluid Mech. 580, 283–301.Google Scholar
36. Niwa, H. S. 1994 Self-organizing dynamic model of fish schooling. J. Theor. Biol. 171 (2), 123–136.Google Scholar
37. Pedley, T. J. & Kessler, J. O. 1992 Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu. Rev. Fluid Mech. 24, 313–358.Google Scholar
38. Pesavento, U. & Wang, Z. J. 2004 Falling paper: Navier–Stokes solutions, model of fluid forces, and centre of mass elevation. Phys. Rev. Lett. 93 (14), 144501.Google Scholar
39. Saintillan, D. & Shelley, M. 2008 Instabilities and pattern formation in active particle suspensions: kinetic theory and continuum simulations. Phys. Rev. Lett 100, 178103.Google Scholar
40. Singh, P., Caussignac, P. H., Fortes, A. F., Joseph, D. D. & Lundgren, T. S. 1989 Stability of periodic arrays of cylinders across the stream by direct numerical simulation. J. Fluid Mech. 205, 553–571.Google Scholar
41. Thiffeault, J.-L. & Childress, S. 2010 Stirring by swimming bodies. Phys. Lett. A 374 (34), 3487–3490.Google Scholar
42. Wang, Z. J. & Russell, D. 2007 Effect of forewing and hindwing interactions on aerodynamic forces and power in hovering dragonfly flight. Phys. Rev. Lett. 99, 148101.CrossRefGoogle ScholarPubMed
43. Warhaft, Z. 2009 Laboratory studies of droplets in turbulence: towards understanding the formation of clouds. Fluid Dyn. Res. 41, 011201.Google Scholar
44. Xu, S. 2008 The immersed interface method for simulating prescribed motion of rigid objects in an incompressible viscous flow. J. Comput. Phys. 227, 5045–5071.Google Scholar
45. Xu, S. & Wang, Z. J. 2006a An immersed interface method for simulating the interaction of a fluid with moving boundaries. J. Comput. Phys. 216, 454–493.Google Scholar
46. Xu, S. & Wang, Z. J. 2006b Systematic derivation of jump conditions for the immersed interface method in three-dimensional flow simulation. SIAM 27 (6), 1948–1980.Google Scholar
47. Xu, S. & Wang, Z. J. 2007 A 3D immersed interface method for fluid–solid interaction. Comput. Meth. Appl. Mech. Engng 197, 2068–2086.CrossRefGoogle Scholar