Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Huang, Wei-Xi
and
Tian, Fang-Bao
2019.
Recent trends and progress in the immersed boundary method.
Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science,
Vol. 233,
Issue. 23-24,
p.
7617.
Alloush, M. M.
Liermann, M.
Zedan, A.
and
Oweis, G. F.
2019.
A Novel Pulse Damper for Endothelial Cell Flow Bioreactors.
Cardiovascular Engineering and Technology,
Vol. 10,
Issue. 1,
p.
95.
Zhu, Chi
Seo, Jung-Hee
and
Mittal, Rajat
2019.
Computational Modeling and Analysis of Murmurs Generated by Modeled Aortic Stenoses.
Journal of Biomechanical Engineering,
Vol. 141,
Issue. 4,
Salameh, Elie
Saade, Charbel
and
Oweis, Ghanem F.
2019.
Experimental Insight into the Hemodynamics and Perfusion of Radiological Contrast in Patent and Non-patent Aortic Dissection Models.
Cardiovascular Engineering and Technology,
Vol. 10,
Issue. 2,
p.
314.
Ozden, Kamil
Sert, Cuneyt
and
Yazicioglu, Yigit
2020.
Effect of stenosis shape on the sound emitted from a constricted blood vessel.
Medical & Biological Engineering & Computing,
Vol. 58,
Issue. 3,
p.
643.
Freidoonimehr, Navid
Arjomandi, Maziar
Sedaghatizadeh, Nima
Chin, Rey
and
Zander, Anthony
2020.
Transitional turbulent flow in a stenosed coronary artery with a physiological pulsatile flow.
International Journal for Numerical Methods in Biomedical Engineering,
Vol. 36,
Issue. 7,
Freidoonimehr, Navid
Chin, Rey
Zander, Anthony
and
Arjomandi, Maziar
2020.
An experimental model for pressure drop evaluation in a stenosed coronary artery.
Physics of Fluids,
Vol. 32,
Issue. 2,
Ozden, Kamil
Yazicioglu, Yigit
and
Sert, Cuneyt
2021.
Simulation of turbulence induced sound generation inside stenosed femoral artery models with different severities and eccentricities.
Computer Methods and Programs in Biomedicine,
Vol. 208,
Issue. ,
p.
106253.
Bailoor, Shantanu
Seo, Jung-Hee
Schena, Stefano
and
Mittal, Rajat
2021.
Detecting Aortic Valve Anomaly From Induced Murmurs: Insights From Computational Hemodynamic Models.
Frontiers in Physiology,
Vol. 12,
Issue. ,
Freidoonimehr, Navid
Arjomandi, Maziar
Zander, Anthony
and
Chin, Rey
2021.
Effect of artery curvature on the coronary fractional flow reserve.
Physics of Fluids,
Vol. 33,
Issue. 3,
Bailoor, Shantanu
Seo, Jung-Hee
Dasi, Lakshmi Prasad
Schena, Stefano
and
Mittal, Rajat
2021.
A computational study of the hemodynamics of bioprosthetic aortic valves with reduced leaflet motion.
Journal of Biomechanics,
Vol. 120,
Issue. ,
p.
110350.
Nitti, A.
De Cillis, G.
and
de Tullio, M.D.
2022.
Numerical investigation of turbulent features past different mechanical aortic valves.
Journal of Fluid Mechanics,
Vol. 940,
Issue. ,
Mourato, André
Valente, Rodrigo
Xavier, José
Brito, Moisés
Avril, Stéphane
de Sá, José César
Tomás, António
and
Fragata, José
2022.
Computational Modelling and Simulation of Fluid Structure Interaction in Aortic Aneurysms: A Systematic Review and Discussion of the Clinical Potential.
Applied Sciences,
Vol. 12,
Issue. 16,
p.
8049.
Zhu, Chi
Seo, Jung-Hee
and
Mittal, Rajat
2022.
Computational Modeling of Aortic Stenosis With a Reduced Degree-of-Freedom Fluid-Structure Interaction Valve Model.
Journal of Biomechanical Engineering,
Vol. 144,
Issue. 3,
Ghasemi Pour, Mohammad Javad
Hassani, Kamran
Khayat, Morteza
and
Etemadi Haghighi, Shahram
2022.
Modeling of aortic valve stenosis using fluid-structure interaction method.
Perfusion,
Vol. 37,
Issue. 4,
p.
367.
Hoeijmakers, M. J. M. M.
Morgenthaler, V.
Rutten, M. C. M.
and
van de Vosse, F. N.
2022.
Scale-Resolving Simulations of Steady and Pulsatile Flow Through Healthy and Stenotic Heart Valves.
Journal of Biomechanical Engineering,
Vol. 144,
Issue. 3,
Seo, Jung Hee
and
Mittal, Rajat
2022.
Computational Modeling of Drug Dissolution in the Human Stomach.
Frontiers in Physiology,
Vol. 12,
Issue. ,
Wu, Fan
Wang, Hongping
Wang, Chunyu
Xu, Duo
and
Wang, Shizhao
2022.
A hydraulic model for flow rate ratio of triple cannulation extracorporeal membrane oxygenation.
Physics of Fluids,
Vol. 34,
Issue. 4,
Deplano, Valérie
and
Guivier‐Curien, Carine
2022.
Biological Flow in Large Vessels.
p.
69.
Mazo, A. B.
Kalinin, E. I.
Molochnikov, V. M.
and
Dushina, O. A.
2022.
Simulation of a pulsating flow in a pipe with local constrictions as applied to hemodynamics of blood vessels.
Thermophysics and Aeromechanics,
Vol. 29,
Issue. 2,
p.
249.
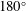 $180^{\circ }$ turn, and three different stenoses with area reductions of 50 %, 62.5 % and 75 % are examined. A uniform steady inlet velocity with a Reynolds number of 2000 is used for all of the cases and direct numerical simulation is employed to resolve the dynamics of the flow. The poststenotic flow is dominated by the jet that originates from the stenosis as well as the secondary flow induced by the curvature, and both contribute significantly to the flow turbulence. On the anterior surface of the modelled aorta, the location with maximum pressure fluctuation, which may be considered as the source location for the murmurs, is found to be located around
$180^{\circ }$ turn, and three different stenoses with area reductions of 50 %, 62.5 % and 75 % are examined. A uniform steady inlet velocity with a Reynolds number of 2000 is used for all of the cases and direct numerical simulation is employed to resolve the dynamics of the flow. The poststenotic flow is dominated by the jet that originates from the stenosis as well as the secondary flow induced by the curvature, and both contribute significantly to the flow turbulence. On the anterior surface of the modelled aorta, the location with maximum pressure fluctuation, which may be considered as the source location for the murmurs, is found to be located around 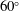 $60^{\circ }$ along the aortic arch, and this location is relatively insensitive to the severity of the stenosis. For all three cases, this high-intensity wall pressure fluctuation includes contributions from both the jet and the secondary flow. Spectral analysis shows that for all three stenoses, the Strouhal number of the vortex shedding of the jet shear layer is close to 0.93, which is higher than the shedding frequency of a corresponding free jet or a jet confined in a straight pipe. This frequency also appears in the pressure spectra at the location postulated as the source of the murmurs, in the form of a ‘break frequency.’ The implications of these findings for cardiac auscultation-based diagnosis of aortic stenosis are also discussed.
$60^{\circ }$ along the aortic arch, and this location is relatively insensitive to the severity of the stenosis. For all three cases, this high-intensity wall pressure fluctuation includes contributions from both the jet and the secondary flow. Spectral analysis shows that for all three stenoses, the Strouhal number of the vortex shedding of the jet shear layer is close to 0.93, which is higher than the shedding frequency of a corresponding free jet or a jet confined in a straight pipe. This frequency also appears in the pressure spectra at the location postulated as the source of the murmurs, in the form of a ‘break frequency.’ The implications of these findings for cardiac auscultation-based diagnosis of aortic stenosis are also discussed.