Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-06T08:26:44.555Z Has data issue: false hasContentIssue false
  • English
  • Français

Computational analysis of physical mechanisms at the onset of three-dimensionality in the wake of a square cylinder

Published online by Cambridge University Press:  07 November 2017

G. Agbaglah Open the ORCID record for G. Agbaglah [Opens in a new window]  and
C. Mavriplis
G. Agbaglah
Affiliation:
Department of Mechanical Engineering, University of Ottawa, 161 Louis Pasteur, Ottawa, ON, K1N 6N5, Canada
C. Mavriplis
Affiliation:
Department of Mechanical Engineering, University of Ottawa, 161 Louis Pasteur, Ottawa, ON, K1N 6N5, Canada
Get access Rights & Permissions [Opens in a new window]

Abstract

A high-order spectral element method is used to perform direct numerical simulations of flow past a square cylinder at the transition from the two-dimensional von Kármán vortex street in the wake of the cylinder to three-dimensionality. A Reynolds number range between 100 and 300 has been considered and good agreement with previous numerical and experimental results is obtained. At transition, the spanwise perturbation observed in the cylinder wake occurs before the onset of the streamwise vortex separation, while the former mechanism is commonly shown, in the literature, to originate from the latter by an instability of the cores or interactions of shed vortices in the vicinity of the cylinder. 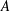It is shown that the first three-dimensional unstable mode, the mode $A$, originates from an axial stretching of the upstream perturbed vorticity, existing on the braids, due to the strain field created by the spanwise vortices which evolve under a shear instability of the wake when viscous effects are small. On the other hand, the mode 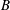$B$ is observed to arise only after spanwise vortices are shed downstream of the cylinder.

JFM classification

Instability: Nonlinear instability Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 833 , 25 December 2017 , pp. 631 - 647
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkley, D. & Henderson, R. D. 1996 Three dimensional Floquet stability analysis of the wake of circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Blackburn, H. M. & Lopez, J. M. 2003 On three-dimensional quasiperiodic Floquet instabilities of two-dimensional bluff body wakes. Phys. Fluids 15, L57–L60.Google Scholar
Blackburn, H. M., Marques, F. & Lopez, J. M. 2005 Symmetry breaking of two-dimensional time-periodic wakes. J. Fluid Mech. 522, 395–411.CrossRefGoogle Scholar
Bloor, M. S. 1964 The transition to turbulence in the wake of a circular cylinder. J. Fluid Mech. 19, 290–304.CrossRefGoogle Scholar
Brede, M., Eckelmann, H. & Rockwell, D. 1996 On secondary vortices in the cylinder wake. Phys. Fluids A 8 (8), 2117–2124.CrossRefGoogle Scholar
Breuer, M., Bernsdorf, J., Zeiser, T. & Durst, F. 2000 Accurate computations of the laminar flow past a square cylinder based on two different methods: lattice Boltzmann and finite-volume. Intl J. Heat Fluid Flow 21, 186–196.Google Scholar
Davis, R. W., Moore, E. F. & Purtell, L. P. 1984 A numerical–experimental study of confined flow around rectangular cylinders. Phys. Fluids 27, 46–59.Google Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 Nek5000: open source spectral element CFD solver http://nek5000.mcs.anl.gov.Google Scholar
Henderson, R. D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.Google Scholar
Lasheras, J. C. & Choi, H. 1988 Three-dimensional instability of a plane free shear layer: an experimental study of the formation and evolution of streamwise vortices. J. Fluid Mech. 189, 53–86.CrossRefGoogle Scholar
Luo, S. C., Chew, Y. T. & Ng, Y. T. 2003 Characteristics of square cylinder wake transition flows. Phys. Fluids 15, 2549–2559.Google Scholar
Luo, S. C., Tong, X. H. & Khoo, B. C. 2007 Transition phenomena in the wake of a square cylinder. J. Fluids Struct. 23, 227–248.CrossRefGoogle Scholar
Pierrehumbert, R. T. & Widnall, S. E. 1982 The two- and three-dimensional instabilities of a spatially periodic shear layer. J. Fluid Mech. 114, 59–82.Google Scholar
Robichaux, J., Balachandar, S. & Vanka, S. P. 1999 Three-dimensional Floquet instability of the wake of square cylinder. Phys. Fluids 11 (3), 560–578.Google Scholar
Roshko, A.1954 On the development of turbulent wakes from vortex streets. NACA Report 1191, National Advisory Committee for Aeronautics, Washington DC.Google Scholar
Roshko, A. 1993 Perspectives on bluff body aerodynamics. J. Wind Engng Ind. Aerodyn. 49, 79–100.CrossRefGoogle Scholar
Saha, A. K., Biswas, G. & Muralidhar, K. 2003 Three-dimensional study of flow past a square cylinder at low Reynolds numbers. Intl J. Heat Fluid Flow 24, 54–56.CrossRefGoogle Scholar
Sheard, G. J., Fitzgerald, M. J. & Ryan, K. 2009 Cylinders with square cross-section: wake instabilities with incidence angle variation. J. Fluid Mech. 630, 34–69.Google Scholar
Sohankar, A., Norberg, C. & Davidson, L. 1999 Simulation of three-dimensional flow around a square cylinder at moderate Reynolds numbers. Phys. Fluids 11, 288–306.Google Scholar
Thompson, M., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12, 190–196.Google Scholar
Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001 The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15, 607–616.CrossRefGoogle Scholar
Vinuesa, R., Schlatter, P., Malm, J., Mavriplis, C. & Henningson, D. S. 2015 Direct numerical simulation of the flow around a wall-mounted square cylinder under various inflow conditions. J. Turbul. 16, 555–587.CrossRefGoogle Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three dimensionality of a cylinder wake. Phys. Fluids 31, 3165–3168.Google Scholar
Williamson, C. H. K. 1996a Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.CrossRefGoogle Scholar
Williamson, C. H. K. 1996b Vortex dynamics in the cylinder wake. Annu. Rev. Fluid. Mech. 28, 477–539.Google Scholar