Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T07:32:38.637Z Has data issue: false hasContentIssue false
  • English
  • Français

Compressible plane turbulent wakes under pressure gradients evolving in a constant area section

Published online by Cambridge University Press:  08 April 2020

Chitrarth Lav Open the ORCID record for Chitrarth Lav [Opens in a new window] ,
Jimmy Philip  and
Richard D. Sandberg
Chitrarth Lav*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
Jimmy Philip
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
Richard D. Sandberg
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

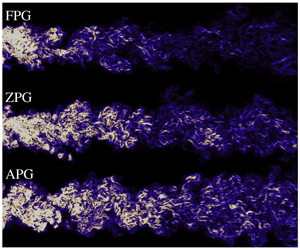
Development of statistically two-dimensional (2-D) turbulent wakes under pressure gradients is a common feature of many industrial and aerodynamic flows. The usual set-up is to generate a wake, and study its development through a passage with a variable area; if the downstream area decreases (increases) a favourable pressure gradient or FPG (adverse pressure gradient or APG) is imposed. In applications such as in turbomachinery, however, the wakes develop in a periodic constant area passage in the stator–rotor gap and with an imposed pressure gradient. To study these flows, here, we develop a canonical set-up for this new kind of wake evolution in FPG and APG of different strengths by placing a 2-D flat plate normal to the flow in a periodic constant area passage and a fixed inflow mass flux. Employing compressible direct numerical simulations, we impose pressure gradients through a ramped body force term to the momentum and total energy equations while the wake is allowed to develop spatially in a region of fixed width. The resultant mean velocity statistics, wake width, energy budgets and entropy generation rates are scrutinised to assess the effect of the pressure gradients, and where possible, the similarities and differences to the conventional case of variable area pressure gradients are discussed. The results show that the effect of a constant area pressure gradient on flow statistics is non-trivial, resulting from significant density changes. The pressure gradients also have an effect on the different energy budgets, which produces a gain for FPG and loss for APG in the mean kinetic energy. Consequently, the entropy generation rate diminishes and augments for the FPG and APG, respectively, compared to the zero pressure gradient. Finally, the effect of different passage heights ($H$) relative to the wake half-width ($\unicode[STIX]{x1D6FF}$) is studied using large eddy simulations. We find that wake width and hence the spreading, depends primarily on the wake–wake interaction for small $H$ and pressure gradients for larger $H$, and this has implications for the design of turbomachinery.

JFM classification

Turbulent Flows: Compressible turbulence Wakes/Jets: Wakes Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 892 , 10 June 2020 , A35
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adamczyk, J. J. 1996 Wake mixing in axial flow compressors. In International Gas Turbine and Aeroengine Congress and Exhibition, pp. 1–12. American Society of Mechanical Engineers.Google Scholar
Adumitroaie, V., Ristorcelli, J. R. & Taulbee, D. B. 1999 Progress in Favré–Reynolds stress closures for compressible flows. Phys. Fluids 11 (9), 2696–2719.CrossRefGoogle Scholar
Bejan, A. 1982 Entropy Generation through Heat and Fluid Flow. Wiley.Google Scholar
Cantwell, B. J.2018 Fundamentals of compressible flow. Available at: https://web.stanford.edu/∼cantwell/AA103_Course_Material/AA210_Fundamentals_of_Compressible_Flow_BOOK_BJ_Cantwell%20copy.pdf.Google Scholar
Chassaing, P., Antonia, R. A., Anselmet, F., Joly, L. & Sarkar, S. 2002 Statistical averaging. In Variable Density Fluid Turbulence, 1st edn (ed. Moreau, R.), chap. 5, pp. 1–387. Springer.CrossRefGoogle Scholar
Cumpsty, N. A. & Horlock, J. H. 2006 Averaging non-uniform flow for a purpose. Trans. ASME J. Turbomach. 128 (January), 120–129.CrossRefGoogle Scholar
Denton, J. D. 1993 Loss mechanisms in turbomachines. Trans. ASME J. Turbomach. 115 (4), 621–656.CrossRefGoogle Scholar
Gartshore, I. 1967 Two-dimensional turbulent wakes. J. Fluid Mech. 30, 547–560.CrossRefGoogle Scholar
George, W. K. 1989 The self-preservation of turbulent flows and its relation to initial conditions and coherent structures. In Advances in Turbulence (ed. George, W. K. & Arndt, R.), chap. 3, pp. 39–73. Hemisphere.Google Scholar
Herwig, H. & Schmandt, B. 2014 How to determine losses in a flow field: a paradigm shift towards the second law analysis. Entropy 16 (6), 2959–2989.CrossRefGoogle Scholar
Hill, P. G., Schaub, U. W. & Sendo, Y. 1963 Turbulent wakes in pressure gradients. Trans. ASME J. Appl. Mech. 30 (4), 518–524.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Kim, J. W. & Sandberg, R. D. 2012 Efficient parallel computing with a compact finite difference scheme. Comput. Fluids 58, 70–87.CrossRefGoogle Scholar
Lav, C., Sandberg, R. D. & Philip, J. 2018 Influence of pressure gradient on plane wake evolution in a constant area section. In Australasian Fluid Mechanics Conference, pp. 1–4. Australasian Fluid Mechanics Society.Google Scholar
Leggett, J., Priebe, S., Shabbir, A., Michelassi, V., Sandberg, R. & Richardson, E. 2018 Loss prediction in an axial compressor cascade at off-design incidences with free stream disturbances using large eddy simulation. Trans. ASME J. Turbomach. 140 (7), 071005.Google Scholar
Lin, D., Yuan, X. & Su, X. 2017 Local entropy generation in compressible flow through a high pressure turbine with delayed detached eddy simulation. Entropy 19 (1), 1–21.CrossRefGoogle Scholar
Liu, X.2001 A study of wake development and structure in constant pressure gradients. PhD thesis, University of Notre Dame, IN.Google Scholar
Liu, X. & Thomas, F. O. 2004 Measurement of the turbulent kinetic energy budget of a planar wake flow in pressure gradients. Exp. Fluids 37 (4), 469–482.CrossRefGoogle Scholar
Liu, X., Thomas, F. O. & Nelson, R. C. 2002 An experimental investigation of the planar turbulent wake in constant pressure gradient. Phys. Fluids 14 (8), 2817–2838.CrossRefGoogle Scholar
Michelassi, V., Chen, L.-w, Pichler, R. & Sandberg, R. D. 2015 Compressible direct numerical simulation of low-pressure turbines. Part II. Effect of inflow disturbances. Trans. ASME J. Turbomach. 137 (July), 1–12.Google Scholar
Nicoud, F. & Ducros, F. 1999 Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 62, 183–200.CrossRefGoogle Scholar
Praisner, T. J., Clark, J. P., Nash, T. C., Rice, M. J. & Grover, E. A. 2006 Performance impacts due to wake mixing in axial-flow turbomachinery. In ASME Turbo Expo 2006, pp. 1–10. ASME.Google Scholar
Rogers, M. M. 2002 The evolution of strained turbulent plane wakes. J. Fluid Mech. 463, 53–120.CrossRefGoogle Scholar
Sandberg, R. D., Michelassi, V., Pichler, R., Chen, L. & Johnstone, R. 2015 Compressible direct numerical simulation of low-pressure turbines—part I: methodology. Trans. ASME J. Turbomach. 137 (5), 051011.Google Scholar
Sandberg, R. D. & Sandham, N. D. 2006 Nonreflecting zonal characteristic boundary condition for direct numerical simulation of aerodynamic sound. AIAA J. 44 (2), 402–405.CrossRefGoogle Scholar
Savitzky, A. & Golay, M. J. E. 1964 Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 36 (8), 1627–1639.CrossRefGoogle Scholar
Schlanderer, S. C., Weymouth, G. D. & Sandberg, R. D. 2016 The boundary data immersion method for compressible flows with application to aeroacoustics. J. Comput. Phys. 333, 440–461.CrossRefGoogle Scholar
Smith, L. H. 1966 Wake dispersion in turbomachines. Trans. ASME J. Basic Engng 88 (3), 688–690.CrossRefGoogle Scholar
Townsend, A. A. 1946 Measurements in the turbulent wake of a cylinder. Proc. R. Soc. Lond. 190 (December), 551–561.Google Scholar
Tummers, M. J., Hanjali, K., Passchier, D. M. & Henkes, R. A. W. M. 2007 Computations of a turbulent wake in a strong adverse pressure gradient. Intl J. Heat Fluid Flow 28 (3), 418–428.CrossRefGoogle Scholar
Wygnanski, I., Champagne, F. & Marasli, B. 1986 On the large-scale structures in two-dimensional, small-deficit, turbulent wakes. J. Fluid Mech. 168, 31–71.CrossRefGoogle Scholar