Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-27T00:23:57.765Z Has data issue: false hasContentIssue false
  • English
  • Français

Complex singularity analysis for vortex layer flows

Published online by Cambridge University Press:  03 December 2021

R.E. Caflisch ,
F. Gargano ,
M. Sammartino Open the ORCID record for M. Sammartino [Opens in a new window]  and
V. Sciacca
R.E. Caflisch
Affiliation:
Courant Institute, 251 Mercer Street, New York, NY 10012-1185, USA
F. Gargano
Affiliation:
Department of Engineering, University of Palermo, Palermo, Italy
M. Sammartino*
Affiliation:
Department of Engineering, University of Palermo, Palermo, Italy
V. Sciacca
Affiliation:
Department of Mathematics, University of Palermo, Palermo, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

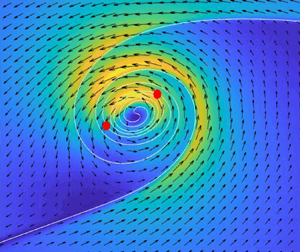
We study the evolution of a 2D vortex layer at high Reynolds number. Vortex layer flows are characterized by intense vorticity concentrated around a curve. In addition to their intrinsic interest, vortex layers are relevant configurations because they are regularizations of vortex sheets. In this paper, we consider vortex layers whose thickness is proportional to the square-root of the viscosity. We investigate the typical roll-up process, showing that crucial phases in the initial flow evolution are the formation of stagnation points and recirculation regions. Stretching and folding characterizes the following stage of the dynamics, and we relate these events to the growth of the palinstrophy. The formation of an inner vorticity core, with vorticity intensity growing to infinity for larger Reynolds number, is the final phase of the dynamics. We display the inner core's self-similar structure, with the scale factor depending on the Reynolds number. We reveal the presence of complex singularities in the solutions of Navier–Stokes equations; these singularities approach the real axis with increasing Reynolds number. The comparison between these singularities and the Birkhoff–Rott singularity seems to suggest that vortex layers, in the limit $Re\rightarrow \infty$, behave differently from vortex sheets.

JFM classification

Boundary Layers: Free shear layers Wakes/Jets: Shear layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 932 , 10 February 2022 , A21
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abarca, S.F. & Corbosiero, K.L. 2005 Secondary eyewall formation in WRF simulations of Hurricanes Rita and Katrina. Geophys. Res. Lett. 38 (7), L07802.Google Scholar
Ayala, D. & Protas, B. 2014 Maximum palinstrophy growth in 2D incompressible flows. J. Fluid Mech. 742, 340–367.CrossRefGoogle Scholar
Bailey, D.H., Borwein, J.M., Crandall, R.E. & Zucker, I.J. 2013 Lattice sums arising from the Poisson equation. J. Phys. A: Math. Theor. 46 (11), 115201.CrossRefGoogle Scholar
Baker, G.R. & Beale, J.T. 2004 Vortex blob methods applied to interfacial motion. J. Comput. Phys. 196 (1), 233–258.CrossRefGoogle Scholar
Baker, G.R., Caflisch, R.E. & Siegel, M. 1993 Singularity formation during Rayleigh–Taylor instability. J. Fluid Mech. 252, 51–75.CrossRefGoogle Scholar
Baker, G.R., Meiron, D.I. & Orszag, S.A. 1982 Generalized vortex methods for free-surface flow problems. J. Fluid Mech. 123, 477–501.CrossRefGoogle Scholar
Baker, G.R. & Nachbin, A. 1998 Stable methods for vortex sheet motion in the presence of surface tension. SIAM J. Sci. Comput. 19, 1737–1736.CrossRefGoogle Scholar
Baker, G.R. & Pham, L.D. 2006 A comparison of blob methods for vortex sheet roll-up. J. Fluid Mech. 547, 297–316.CrossRefGoogle Scholar
Baker, G.R. & Shelley, M.J. 1990 On the connection between thin vortex layers and vortex sheets. J. Fluid Mech. 215, 161–194.CrossRefGoogle Scholar
Baker, G.R. & Xie, C. 2011 Singularities in the complex physical plane for deep water waves. J. Fluid Mech. 658, 83–116.CrossRefGoogle Scholar
Bardos, C., Linshiz, J.S. & Titi, È.S. 2008 Global regularity for a Birkhoff–Rott-$\alpha$ approximation of the dynamics of vortex sheets of the 2D Euler equations. Physica D 237 (14–17), 1905–1911.CrossRefGoogle Scholar
Bardos, C., Linshiz, J.S. & Titi, È.S. 2010 Global regularity and convergence of a Birkhoff–Rott-$\alpha$ approximation of the dynamics of vortex sheets of the two-dimensional Euler equations. Commun. Pure Appl. Maths 63 (6), 697–746.CrossRefGoogle Scholar
Benedetto, D. & Pulvirenti, M. 1992 From vortex layers to vortex sheets. SIAM J. Appl. Maths 52 (4), 1041–1056.CrossRefGoogle Scholar
Brady, M. & Pullin, D.I. 1999 On singularity formation in three-dimensional vortex sheet evolution. Phys. Fluids 11 (11), 3198–3200.CrossRefGoogle Scholar
Caflisch, R.E. 1993 Singularity formation for complex solutions of the 3D incompressible Euler equations. Physica D 67 (1–3), 1–18.CrossRefGoogle Scholar
Caflisch, R.E., Gargano, F., Sammartino, M. & Sciacca, V. 2015 Complex singularities and PDEs. Rivista di Matematica della Università di Parma 6 (1), 69–133.Google Scholar
Caflisch, R.E., Gargano, F., Sammartino, M. & Sciacca, V. 2017 Regularized Euler-$\alpha$ motion of an infinite array of vortex sheets. Boll. Unione Mat. Ital. 10 (1), 113–141.CrossRefGoogle Scholar
Caflisch, R.E., Lombardo, M.C. & Sammartino, M.M.L. 2020 Vortex layers of small thickness. Commun. Pure Appl. Maths 73 (10), 2104–2179.CrossRefGoogle Scholar
Caflisch, R.E. & Orellana, O.F. 1989 Singular solutions and ill-posedness for the evolution of vortex sheets. SIAM J. Math. Anal. 20 (2), 293–307.CrossRefGoogle Scholar
Carrier, G.F., Krook, M. & Pearson, C.E. 1966 Functions of a Complex Variable: Theory and Technique. McGraw–Hill.Google Scholar
Catrakis, H.J. & Dimotakis, P.E. 1996 Mixing in turbulent jets: scalar measures and isosurface geometry. J. Fluid Mech. 317, 396–406.CrossRefGoogle Scholar
Chen, M.J. & Forbes, L.K. 2011 Accurate methods for computing inviscid and viscous Kelvin–Helmholtz instability. J. Comput. Phys. 230 (4), 1499–1515.CrossRefGoogle Scholar
Cook, A.W. & Dimotakis, P.E. 2001 Transition stages of Rayleigh–Taylor instability between miscible fluids. J. Fluid Mech. 443, 69–99.CrossRefGoogle Scholar
Cowley, S.J., Baker, G.R. & Tanveer, S. 1999 On the formation of Moore curvature singularities in vortex sheets. J. Fluid Mech. 378, 233–267.CrossRefGoogle Scholar
Delort, J.-M. 1991 Existence de nappes de tourbillon en dimension deux. J. Am. Math. Soc. 4 (3), 553–586.CrossRefGoogle Scholar
DeVoria, A.C. & Mohseni, K. 2018 Vortex sheet roll-up revisited. J. Fluid Mech. 855, 299–321.CrossRefGoogle Scholar
Dhanak, M.R. 1994 Equation of motion of a diffusing vortex sheet. J. Fluid Mech. 269, 265–281.CrossRefGoogle Scholar
Dimotakis, P.E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.CrossRefGoogle Scholar
Dimotakis, P.E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.CrossRefGoogle Scholar
DiPerna, R.J. & Majda, A.J. 1987 a Concentrations in regularizations for $2$-D incompressible flow. Commun. Pure Appl. Maths 40 (3), 301–345.CrossRefGoogle Scholar
DiPerna, R.J. & Majda, A.J. 1987 b Oscillations and concentrations in weak solutions of the incompressible fluid equations. Commun. Math. Phys. 108 (4), 667–689.CrossRefGoogle Scholar
Duchon, J. & Robert, R. 1988 Global vortex sheet solutions of Euler equations in the plane. J. Differ. Equ. 73 (2), 215–224.CrossRefGoogle Scholar
Ely, J.S. & Baker, G.R. 1993 High-precision calculations of vortex sheet motion. J. Comput. Phys. 111, 275–281.CrossRefGoogle Scholar
Fjordholm, U.S., Mishra, S. & Tadmor, E. 2016 On the computation of measure-valued solutions. Acta Numerica 25, 567–679.CrossRefGoogle Scholar
Frisch, U., Matsumoto, T. & Bec, J. 2003 Singularities of Euler flow? Not out of the blue! J. Stat. Phys. 113 (5), 761–781.CrossRefGoogle Scholar
Gargano, F., Sammartino, M. & Sciacca, V. 2009 Singularity formation for Prandtl's equations. Physica D 238 (19), 1975–1991.CrossRefGoogle Scholar
Gargano, F., Sammartino, M. & Sciacca, V. 2011 High Reynolds number Navier–Stokes solutions and boundary layer separation induced by a rectilinear vortex. Comput. Fluids 52, 73–91.CrossRefGoogle Scholar
Gargano, F., Sammartino, M., Sciacca, V. & Cassel, K.W. 2014 Analysis of complex singularities in high-Reynolds-number Navier–Stokes solutions. J. Fluid Mech. 747, 381–421.CrossRefGoogle Scholar
Hoepffner, J., Blumenthal, R. & Zaleski, S. 2011 Self-similar wave produced by local perturbation of the Kelvin–Helmholtz shear-layer instability. Phys. Rev. Lett. 106, 104502.CrossRefGoogle ScholarPubMed
van der Hoeven, J. 2009 Algorithms for asymptotic extrapolation. J. Symb. Comput. 44 (8), 1000–1016.CrossRefGoogle Scholar
Holm, D.D., Nitsche, M. & Putkaradze, V. 2006 Euler-alpha and vortex blob regularization of vortex filament and vortex sheet motion. J. Fluid Mech. 555, 149–176.CrossRefGoogle Scholar
Hou, T.Y., Lowengrub, J.S. & Shelley, M.J. 1997 The long-time motion of vortex sheets with surface tension. Phys. Fluids 9 (7), 1933–1954.CrossRefGoogle Scholar
Ishihara, T. & Kaneda, Y. 1995 Singularity formation in three-dimensional motion of a vortex sheet. J. Fluid Mech. 300, 339–366.CrossRefGoogle Scholar
Kimura, Y. & Herring, J.R. 2001 Gradient enhancement and filament ejection for a non-uniform elliptic vortex in two-dimensional turbulence. J. Fluid Mech. 439, 43–56.CrossRefGoogle Scholar
Krasny, R. 1986 a Desingularization of periodic vortex sheet roll-up. J. Comput. Phys. 65 (2), 292–313.CrossRefGoogle Scholar
Krasny, R. 1986 b A study of singularity formation in a vortex sheet by the point-vortex approximation. J. Fluid Mech. 167, 65–93.CrossRefGoogle Scholar
Krasny, R. & Nitsche, M. 2002 The onset of chaos in vortex sheet flow. J. Fluid Mech. 454, 47–69.CrossRefGoogle Scholar
Liu, J.G. & Xin, Z. 1995 Convergence of vortex methods for weak solutions to the 2D Euler equations with vortex sheet data. Commun. Pure Appl. Maths 48, 611–628.CrossRefGoogle Scholar
Lopes Filho, M.C., Nussenzveig Lopes, H.J. & Xin, Z. 2001 Existence of vortex sheets with reflection symmetry in two space dimensions. Arch. Rat. Mech. Anal. 158 (3), 235–257.CrossRefGoogle Scholar
Lopes Filho, M.C., Lowengrub, J., Nussenzveig Lopes, H.J. & Zheng, Y. 2006 Numerical evidence of nonuniqueness in the evolution of vortex sheets. ESAIM: Math. Model. Num. Anal. 40 (2), 225–237.CrossRefGoogle Scholar
Lopes Filho, M.C., Nussenzveig Lopes, H.J. & Shochet, S. 2007 A criterion for the equivalence of the Birkhoff–Rott and Euler descriptions of vortex sheet evolution. Trans. Am. Math. Soc. 359, 4125–4142.CrossRefGoogle Scholar
Majda, A.J. 1993 Remarks on weak solutions for vortex sheets with a distinguished sign. Indiana Univ. Math. J. 42, 921–939.CrossRefGoogle Scholar
Malakuti, K., Caflisch, R.E., Siegel, M. & Virodov, A. 2013 Detection of complex singularities for a function of several variables. IMA J. Appl. Maths 78 (4), 714–728.CrossRefGoogle Scholar
Mengual, F. & Székelyhidi, L. 2020 Dissipative Euler flows for vortex sheet initial data without distinguished sign. arXiv:2005.08333.Google Scholar
Moore, D.W. 1978 The equation of motion of a vortex layer of small thickness. Stud. Appl. Maths 58 (2), 119–140.CrossRefGoogle Scholar
Moore, D.W. 1979 The spontaneous appearance of a singularity in the shape of an evolving vortex sheet. Proc. R. Soc. Lond. A 365 (1720), 105–119.Google Scholar
Moore, D.W. 1985 Numerical and analytical aspects of Helmholtz instability. In Proceedings of the Sixteenth International Congress of Theoretical and Applied Mechanics, Lyngby, Denmark (ed. F.I. Niordson & N. Olhoff), pp. 263–274. Elsevier, North-Holland.CrossRefGoogle Scholar
Nguyen Van Yen, N., Waidmann, M., Klein, R., Farge, M. & Schneider, K. 2018 Energy dissipation caused by boundary layer instability at vanishing viscosity. J. Fluid Mech. 849, 676–717.CrossRefGoogle Scholar
Nitsche, M. 2001 Singularity formation in a cylindrical and a spherical vortex sheet. J. Comput. Phys. 173 (1), 208–230.CrossRefGoogle Scholar
Nitsche, M., Taylor, M.A. & Krasny, R. 2003 Comparison of regularizations of vortex sheet motion. In Computational Fluid and Solid Mechanics Vol. 1, Proceedings of the 2nd MIT Conference held in Cambridge, MA, June 17–20, 2003 (ed. K.J. Bathe), pp. 1062–1065. Elsevier Science Ltd.CrossRefGoogle Scholar
Pauls, W. & Frisch, U. 2007 A Borel transform method for locating singularities of Taylor and Fourier series. J. Stat. Phys. 127 (6), 1095–1119.CrossRefGoogle Scholar
Pauls, W., Matsumoto, T., Frisch, U. & Bec, J. 2006 Nature of complex singularities for the 2D Euler equation. Physica D 219 (1), 40–59.CrossRefGoogle Scholar
Pugh, M.C. & Shelley, M.J. 1998 Singularity formation in thin jets with surface tension. Commun. Pure Appl. Maths 51 (7), 733–795.3.0.CO;2-7>CrossRefGoogle Scholar
Pullin, D.I. 1989 On similarity flows containing two-branched vortex sheets. In Mathematical Aspects of Vortex Dynamics (ed. R.E. Caflisch), pp. 97–106. Philadelphia, PA, SIAM.Google Scholar
Schlichting, H. 1960 Boundary Layer Theory. McGraw-Hill Book Co. Inc.Google Scholar
Schochet, S. 1995 The weak vorticity formulation of the 2-D Euler equations and concentration-cancellation. Commun. Part. Differ. Equ. 20 (5), 1077–1104.CrossRefGoogle Scholar
Schubert, W.H., Montgomery, M.T., Taft, R.K., Guinn, T.A., Fulton, S.R., Kossin, J.P. & Edwards, J.P. 1999 Polygonal eyewalls, asymmetric eye contraction, and potential vorticity mixing in hurricanes. J. Atmos. Sci. 56, 1197–1223.2.0.CO;2>CrossRefGoogle Scholar
Shelley, M.J. 1992 A study of singularity formation in vortex–sheet motion by a spectrally accurate vortex method. J. Fluid. Mech. 244, 493–526.CrossRefGoogle Scholar
Siegel, M. & Caflisch, R.E. 2009 Calculation of complex singular solutions to the 3D incompressible Euler equations. Physica D 238 (23–24), 2368–2379.CrossRefGoogle Scholar
Sohn, S.-I. 2011 Inviscid and viscous vortex models for Richtmyer–Meshkov instability. Fluid Dyn. Res. 43 (6), 065506.CrossRefGoogle Scholar
Sohn, S.-I. 2013 Singularity formation and nonlinear evolution of a viscous vortex sheet model. Phys. Fluids 25 (1), 014106.CrossRefGoogle Scholar
Sohn, S.-I. 2014 Two vortex-blob regularization models for vortex sheet motion. Phys. Fluids 26 (4), 044105.CrossRefGoogle Scholar
Sohn, S.-I. 2016 Self-similar roll-up of a vortex sheet driven by a shear flow: hyperbolic double spiral. Phys. Fluids 28 (6), 064104.CrossRefGoogle Scholar
Sulem, C., Sulem, P.-L. & Frisch, H. 1983 Tracing complex singularities with spectral methods. J. Comput. Phys. 50 (1), 138–161.CrossRefGoogle Scholar
Székelyhidi, L. 2011 Weak solutions to the incompressible Euler equations with vortex sheet initial data. C. R. Math. 349 (19), 1063–1066.CrossRefGoogle Scholar
Tryggvason, G., Dahm, W.J.A. & Sbeih, K. 1991 Fine structure of vortex sheet rollup by viscous and inviscid simulation. Trans. ASME J. Fluids Engng 113 (1), 31–36.CrossRefGoogle Scholar
Widmann, A. & Tropea, C. 2015 Parameters influencing vortex growth and detachment on unsteady aerodynamic profiles. J. Fluid Mech. 773, 432–459.CrossRefGoogle Scholar
Zhong, X. 1996 Additive semi-implicit Runge–Kutta methods for computing high-speed nonequilibrium reactive flows. J. Comput. Phys. 128 (1), 19–31.CrossRefGoogle Scholar

Caflisch et al. supplementary movie 1

See pdf file for movie caption
Download Caflisch et al. supplementary movie 1(Video)
Video 11.6 MB

Caflisch et al. supplementary movie 2

See pdf file for movie caption

Download Caflisch et al. supplementary movie 2(Video)
Video 14 MB
Supplementary material: PDF

Caflisch et al. suppementary material

Captions for movies 1-2

Download Caflisch et al. suppementary material(PDF)
PDF 11.1 KB