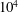Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-03T20:54:15.889Z Has data issue: false hasContentIssue false
  • English
  • Français

A comparative study of the velocity and vorticity structure in pipes and boundary layers at friction Reynolds numbers up to $10^{4}$

Published online by Cambridge University Press:  23 April 2019

S. Zimmerman Open the ORCID record for S. Zimmerman [Opens in a new window] ,
J. Philip Open the ORCID record for J. Philip [Opens in a new window] ,
J. Monty Open the ORCID record for J. Monty [Opens in a new window] ,
A. Talamelli Open the ORCID record for A. Talamelli [Opens in a new window] ,
I. Marusic Open the ORCID record for I. Marusic [Opens in a new window] ,
B. Ganapathisubramani Open the ORCID record for B. Ganapathisubramani [Opens in a new window] ,
R. J. Hearst Open the ORCID record for R. J. Hearst [Opens in a new window] ,
G. Bellani Open the ORCID record for G. Bellani [Opens in a new window] ,
R. Baidya Open the ORCID record for R. Baidya [Opens in a new window]  and
M. Samie Open the ORCID record for M. Samie [Opens in a new window]
...Show all authors
S. Zimmerman*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
J. Philip
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
J. Monty
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
A. Talamelli
Affiliation:
DIN, Alma Mater Studiorum – Università di Bologna, I-47100 Forli, Italy
I. Marusic
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
B. Ganapathisubramani
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Southapton SO17 1BJ, UK
R. J. Hearst
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Southapton SO17 1BJ, UK Department of Energy and Process Engineering, Norwegian University of Science and Technology, Trondheim NO-7491, Norway
G. Bellani
Affiliation:
DIN, Alma Mater Studiorum – Università di Bologna, I-47100 Forli, Italy
R. Baidya
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
M. Samie
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
X. Zheng
Affiliation:
DIN, Alma Mater Studiorum – Università di Bologna, I-47100 Forli, Italy
E. Dogan
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Southapton SO17 1BJ, UK
L. Mascotelli
Affiliation:
DIN, Alma Mater Studiorum – Università di Bologna, I-47100 Forli, Italy
J. Klewicki
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This study presents findings from a first-of-its-kind measurement campaign that includes simultaneous measurements of the full velocity and vorticity vectors in both pipe and boundary layer flows under matched spatial resolution and Reynolds number conditions. Comparison of canonical turbulent flows offers insight into the role(s) played by features that are unique to one or the other. Pipe and zero pressure gradient boundary layer flows are often compared with the goal of elucidating the roles of geometry and a free boundary condition on turbulent wall flows. Prior experimental efforts towards this end have focused primarily on the streamwise component of velocity, while direct numerical simulations are at relatively low Reynolds numbers. In contrast, this study presents experimental measurements of all three components of both velocity and vorticity for friction Reynolds numbers 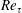$Re_{\unicode[STIX]{x1D70F}}$ ranging from 5000 to 10 000. Differences in the two transverse Reynolds normal stresses are shown to exist throughout the log layer and wake layer at Reynolds numbers that exceed those of existing numerical data sets. The turbulence enstrophy profiles are also shown to exhibit differences spanning from the outer edge of the log layer to the outer flow boundary. Skewness and kurtosis profiles of the velocity and vorticity components imply the existence of a ‘quiescent core’ in pipe flow, as described by Kwon et al. (J. Fluid Mech., vol. 751, 2014, pp. 228–254) for channel flow at lower 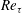$Re_{\unicode[STIX]{x1D70F}}$, and characterize the extent of its influence in the pipe. Observed differences between statistical profiles of velocity and vorticity are then discussed in the context of a structural difference between free-stream intermittency in the boundary layer and ‘quiescent core’ intermittency in the pipe that is detectable to wall distances as small as 5 % of the layer thickness.

JFM classification

Boundary Layers: Boundary layer structure Boundary Layers: Pipe flow boundary layer Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 869 , 25 June 2019 , pp. 182 - 213
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A., Zhou, T. & Zhu, Y. 1998 Three-component vorticity measurements in a turbulent grid flow. J. Fluid Mech. 374, 29–57.Google Scholar
Baidya, R.2015 Multi-component velocity measurements in turbulent boundary layers. PhD thesis, University of Melbourne.Google Scholar
Bradshaw, P. 1971 An Introduction to Turbulence and its Measurement. Pergamon Press.Google Scholar
Chauhan, K., Philip, J. & Marusic, I. 2014a Scaling of the turbulent/non-turbulent interface in boundary layers. J. Fluid Mech. 751, 298–328.Google Scholar
Chauhan, K., Philip, J., de Silva, C. M., Hutchins, N. & Marusic, I. 2014b The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.Google Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.Google Scholar
Chin, C., Monty, J. P. & Ooi, A. 2014 Reynolds number effects in DNS of pipe flow and comparison with channels and boundary layers. Intl J. Heat Fluid Flow 45, 33–40.Google Scholar
El Khoury, G. K., Schlatter, P., Noorani, A., Fischer, P. F., Brethouwer, G. & Johansson, A. V. 2013 Direct numerical simulation of turbulent pipe flow at moderately high Reynolds numbers. Flow Turbul. Combust. 91 (3), 475–495.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18 (1), 011702.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.Google Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.Google Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335.Google Scholar
Jorgensen, F. E. 1971 Directional sensitivity of wire and fiber-film probes. DISA Information 11 (3), 1–7.Google Scholar
Klebanoff, P. S.1955 Characteristics of turbulence in boundary layer with zero pressure gradient. NACA Tech. Rep. 1247.Google Scholar
Kulandaivelu, V.2012 Evolution of zero pressure gradient turbulent boundary layers from different initial conditions. PhD thesis, University of Melbourne.Google Scholar
Kwon, Y. S., Philip, J., de Silva, C. M., Hutchins, N. & Monty, J. P. 2014 The quiescent core of turbulent channel flow. J. Fluid Mech. 751, 228–254.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Marusic, I., Chauhan, K. A., Kulandaivelu, V. & Hutchins, N. 2015 Evolution of zero-pressure-gradient boundary layers from different tripping conditions. J. Fluid Mech. 783, 379–411.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
McKeon, B. J., Swanson, C. J., Zagarola, M. V., Donnelly, R. J. & Smits, A. J. 2004 Friction factors for smooth pipe flow. J. Fluid Mech. 511, 41–44.Google Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7 (4), 694–696.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
Morrill-Winter, C.2016 Structure of mean dynamics and spanwise vorticity in turbulent boundary layers. PhD thesis, University of Melbourne.Google Scholar
Morrill-Winter, C. & Klewicki, J. 2013 Influences of boundary layer scale separation on the vorticity transport contribution to turbulent inertia. Phys. Fluids 25 (1), 015108.Google Scholar
Morrill-Winter, C., Klewicki, J., Baidya, R. & Marusic, I. 2015 Temporally optimized spanwise vorticity sensor measurements in turbulent boundary layers. Exp. Fluids 56 (12), 1–14.Google Scholar
Morrill-Winter, C., Philip, J. & Klewicki, J. 2017 Statistical evidence of anasymptotic geometric structure to the momentum transporting motions in turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 375 (2089), 20160084.Google Scholar
Örlü, R., Fiorini, T., Segalini, A., Bellani, G., Talamelli, A. & Alfredsson, P. H. 2017 Reynolds stress scaling in pipe flow turbulence—first results from CICLoPE. Phil. Trans. R. Soc. Lond. A 375 (2089), 20160187.Google Scholar
Samie, M., Marusic, I., Hutchins, N., Fu, M. K., Fan, Y., Hultmark, M. & Smits, A. J. 2018 Fully resolved measurements of turbulent boundary layer flows up to Re 𝜏 = 20 000. J. Fluid Mech. 851, 391–415.Google Scholar
Schubauer, G. B. 1954 Turbulent processes as observed in boundary layer and pipe. J. Appl. Phys. 25 (2), 188–196.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 25 (10), 105102.Google Scholar
Talamelli, A., Persiani, F., Fransson, J. H. M., Alfredsson, P. H., Johansson, A. V., Nagib, H. M., Rüedi, J.-D., Sreenivasan, K. R. & Monkewitz, P. A. 2009 CICLoPE—a response to the need for high Reynolds number experiments. Fluid Dyn. Res. 41 (2), 021407.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. The MIT Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Vincenti, P., Klewicki, J., Morrill-Winter, C., White, C. M. & Wosnik, M. 2013 Streamwise velocity statistics in turbulent boundary layers that spatially develop to high Reynolds number. Exp. Fluids 54 (12), 1629.Google Scholar
Wallace, J. M. & Vukoslavčević, P. V. 2010 Measurement of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 42, 157–181.Google Scholar
Zhu, Y. & Antonia, R. A. 1995 The spatial resolution of two x-probes for velocity derivative measurements. Meas. Sci. Technol. 6 (5), 538.Google Scholar
Zimmerman, S., Morrill-Winter, C. & Klewicki, J. 2017 Design and implementation of a hot-wire probe for simultaneous velocity and vorticity vector measurements in boundary layers. Exp. Fluids 58 (10), 148.Google Scholar