Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T16:43:00.790Z Has data issue: false hasContentIssue false
  • English
  • Français

Columnar vortices induced by dielectrophoretic force in a stationary cylindrical annulus filled with a dielectric liquid

Published online by Cambridge University Press:  15 December 2020

Changwoo Kang Open the ORCID record for Changwoo Kang [Opens in a new window]  and
Innocent Mutabazi Open the ORCID record for Innocent Mutabazi [Opens in a new window]
Changwoo Kang
Affiliation:
Laboratoire Ondes et Milieux Complexes (LOMC), UMR 6294, Normandie Université, UNIHAVRE, CNRS-Université du Havre, 53 Rue de Prony, CS 80540, 76058Le Havre CEDEX, France Department of Mechanical Engineering, Jeonbuk National University, 567 Baekje-daero, Deokjin-gu, Jeonju-si, Jeollabuk-do, 54896, Republic of Korea
Innocent Mutabazi*
Affiliation:
Laboratoire Ondes et Milieux Complexes (LOMC), UMR 6294, Normandie Université, UNIHAVRE, CNRS-Université du Havre, 53 Rue de Prony, CS 80540, 76058Le Havre CEDEX, France
*
† Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

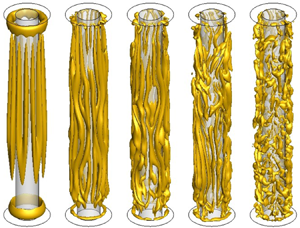
The dynamics of flow of a dielectric fluid in a vertical cylindrical annulus with a fixed temperature difference and an increasing alternating electric tension has been investigated using a direct numerical simulation (DNS). The temperature difference imposed on the cylindrical surfaces induces a radial temperature gradient perpendicular to the ground gravity which generates a baroclinic flow ascending near the hot surface and descending near the cold one. The electric field coupled with the permittivity gradient generates a dielectrophoretic buoyancy force which is a source of vorticity. Above a critical value of the electric tension, the flow bifurcates to a pattern of stationary columnar vortices. These columnar vortices which characterize the thermoelectric convection are not axially invariant, in contrast with classical Taylor columns. They bifurcate to regular wave patterns and then to spatio-temporal chaotic patterns when the electric field intensity is increased. The flow and temperature fields, the kinetic energy and the enstrophy of thermoelectric convective regimes are computed for different values of the electric tension.

JFM classification

Complex Fluids: Dielectrics Convection: Buoyancy-driven instability Nonlinear Dynamical Systems: Pattern formation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 908 , 10 February 2021 , A26
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ali, M. & McFadden, G. B. 2005 Linear stability of cylindrical Couette flow in the convection regime. Phys. Fluids 17, 054112.CrossRefGoogle Scholar
Alonso, A., Net, M. & Knobloch, E. 1995 On the transition to columnar convection. Phys. Fluids 7, 935–940.CrossRefGoogle Scholar
Alonso, A., Net, M., Mercader, I. & Knobloch, E. 1999 Onset of convection in a rotating annulus with radial gravity and heating. Fluid Dyn. Res. 24 (3), 133–145.CrossRefGoogle Scholar
Atten, P. & Elouadie, L. 1995 EHD convection in a dielectric liquid subjected to unipolar injection: coaxial wire/cylinder geometry. J. Electrostat. 34, 279–297.CrossRefGoogle Scholar
Auer, M., Busse, F. H. & Clever, R. M. 1995 Three-dimensional convection driven by centrifugal buoyancy. J. Fluid Mech. 301, 371–382.CrossRefGoogle Scholar
Bahloul, A., Mutabazi, I. & Ambari, A. 2000 Codimension 2 points in the flow inside a cylindrical annulus with a radial temperature gradient. Eur. Phys. J. Appl. Phys. 9 (3), 253–264.CrossRefGoogle Scholar
Barbic, M., Mock, J. J., Gray, A. P. & Schultz, S. 2001 Electromagnetic micromotor for microfluidics applications. Appl. Phys. Lett. 79 (9), 1399–1401.CrossRefGoogle Scholar
Bird, R. B., Stewart, W. E. & Lightfoot, E. N. 1960 Transport Phenomena, 2nd edn. John Wiley & Sons.Google Scholar
Bot, P., Cadot, O. & Mutabazi, I. 1998 Secondary instability mode of a roll pattern and transition to spatiotemporal chaos in the Taylor-Dean system. Phys. Rev. E 58 (3), 3089–3097.CrossRefGoogle Scholar
Bot, P. & Mutabazi, I. 2000 Dynamics of spatio-temporal defects in the Taylor-Dean system. Eur. Phys. J. B 13, 141–155.CrossRefGoogle Scholar
Busse, F. H. & Carrigan, C. R. 1974 Convection induced by centrifugal buoyancy. J. Fluid Mech. 62, 579–592.CrossRefGoogle Scholar
Chandra, B. & Smylie, D. E. 1972 A laboratory model of thermal convection under a central force field. Geophys. Fluid Dyn. 3 (3), 211–224.CrossRefGoogle Scholar
Cross, M. C. & Hohenberg, P. C. 1993 Pattern formation outside of equilibrium. Rev. Mod. Phys. 65 (3), 851–1112.CrossRefGoogle Scholar
Dahley, N., Futterer, B., Egbers, C., Crumeyrolle, O. & Mutabazi, I. 2011 Parabolic flight experiment “Convection in a Cylinder” - convection patterns in varying buoyancy forces. J. Phys: Conf. Ser. 318, 082003.Google Scholar
Davidson, P. A. 2013 Turbulence in Rotating, Stratified and Electrically Conducting Fluids. Cambridge University Press.CrossRefGoogle Scholar
Futterer, B., Gellert, M., Von Larcher, T. & Egbers, C. 2008 Thermal convection in rotating spherical shells: an experimental and numerical approach within GeoFlow. Acta Astronaut. 62, 300–307.CrossRefGoogle Scholar
Futterer, B., Kerbs, A., Plesa, A.-C., Zaussinger, F., Hollerbach, R., Breuer, D. & Egbers, C. 2013 Sheet-like and plume-like thermal flow in a spherical convection experiment performed under microgravity. J. Fluid Mech. 735, 647–683.CrossRefGoogle Scholar
Ghil, M., Read, P. & Smith, L. 2010 Geophyiscal flows as dynamical systems: the influence of Hide's experiments. Astron. Geophys. 51, 4.28–4.35.CrossRefGoogle Scholar
Hart, J. E., Glatzmaier, G. A. & Toomre, J. 1986 Space-laboratory and numerical simulations of thermal convection in a rotating hemispherical shell with radial gravity. J. Fluid Mech. 173, 519–544.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Kang, C., Meyer, A., Yoshikawa, H. N. & Mutabazi, I. 2017 Numerical simulation of circular Couette flow under a radial thermo-electric body force. Phys. Fluids 29, 114105.CrossRefGoogle Scholar
Kang, C., Meyer, A., Yoshikawa, H. N. & Mutabazi, I. 2019 a Numerical study of thermal convection induced by centrifugal buoyancy in a rotating cylindrical annulus. Phys. Rev. Fluids 4, 043501.CrossRefGoogle Scholar
Kang, C., Meyer, A., Yoshikawa, H. N. & Mutabazi, I. 2019 b Thermoelectric convection in a dielectric liquid inside a cylindrical annulus with a solid-body rotation. Phys. Rev. Fluids 4, 093502.CrossRefGoogle Scholar
Kang, C. & Mutabazi, I. 2019 Dielectrophoretic buoyancy and heat transfer in a dielectric liquid contained in a cylindrical annular cavity. J. Appl. Phys. 125, 184902.CrossRefGoogle Scholar
Kang, C., Yang, K.-S. & Mutabazi, I. 2015 Thermal effect on large-aspect-ratio Couette-Taylor system: numerical simulation. J. Fluid Mech. 771, 57–78.CrossRefGoogle Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier-Stokes equations. J. Comput. Phys. 59, 308–323.CrossRefGoogle Scholar
Landau, L. & Lifshitz, E. 1984 Electrodynamics of Continous Media. Volume 8 in Course of Theoretical Physics, 2nd edn. Elsevier Buttherwoth-Heinemann.Google Scholar
Landau, L. & Lifshitz, E. 2000 Mechanics. Volume 1 in Course of Theoretical Physics, 2nd edn. Elsevier Buttherwoth-Heinemann.Google Scholar
Lappa, M. 2012 Rotating Thermal Flows in Natural and Industrial Processes. John Wiley & Sons.CrossRefGoogle Scholar
Le Quéré, P. & Abcha, F. 1990 Sur une classe de solutions exactes des équations de Navier-Stokes du fluide de Boussinesq. C.R. Acad. Sci. Paris 310 (Série II), 353–359.Google Scholar
Lin, H. 2009 Electrokinetic instability in microchannel flows: a review. Mech. Res. Commun. 36, 33–38.CrossRefGoogle Scholar
Lopez, J. M., Marques, F. & Avila, M. 2015 Conductive and convective heat transfer in fluid flows between differentially heated and rotating cylinders. Intl J. Heat Mass Transfer 90, 959–967.CrossRefGoogle Scholar
Malik, S. V., Yoshikawa, H. N., Crumeyrolle, O. & Mutabazi, I. 2012 Thermo-electro-hydro-dynamic instabilities in a dielectric liquid under microgravity. Acta Astronaut. 81, 563–569.CrossRefGoogle Scholar
Manneville, P. 1990 Dissipative Structures and Weak Turbulence. Academic.Google Scholar
McCluskey, F. M. J., Atten, P. & Perez, A. T. 1991 Heat transfer enhancement by electroconvection resulting from an injected space charge between parallel plates. Intl J. Heat Mass Transfer 34, 2237–2250.CrossRefGoogle Scholar
Meier, M., Jongmanns, M., Meyer, A., Seelig, T., Egbers, C. & Mutabazi, I. 2018 Flow pattern and heat transfer in a cylindrical annulus under 1 g and low-g conditions: experiments. Microgravity Sci. Technol. 30 (5), 699–712.CrossRefGoogle Scholar
Melcher, J. R. 1981 Continuum Electromechanics. MIT Press.Google Scholar
Meyer, A., Crumeyrolle, O., Mutabazi, I., Meier, M., Yongmanns, M., Renoult, M.-C., Seelig, T. & Egbers, C. 2018 Flow patterns and heat transfer in a cylindrical annulus under 1 g and low-g conditions: theory and simulation. Microgravity Sci. Technol. 30 (5), 653–662.CrossRefGoogle Scholar
Meyer, A., Jongmanns, M., Meier, M., Egbers, C. & Mutabazi, I. 2017 Thermal convection in a cylindrical annulus under a combined effect of the radial and vertical gravity. CR Mécanique 345, 11–20.CrossRefGoogle Scholar
Meyer, A., Meier, M., Jongmanns, M., Seelig, T., Egbers, C. & Mutabazi, I. 2019 Effect of initial conditions on the growth of thermoelectric instabilities during parabolic flights. Microgravity Sci. Technol. 31 (5), 715–721.CrossRefGoogle Scholar
Mutabazi, I., Yoshikawa, H. N., Tadie Fogaing, M., Travnikov, V., Crumeyrolle, O., Futterer, B. & Egbers, C. 2016 Thermo-electro-hydrodynamic convection under microgravity: a review. Fluid Dyn. Res. 48, 061413.CrossRefGoogle Scholar
Plaut, E. & Busse, F. H. 2002 Low-Prandtl-number convection in a rotating cylindrical annulus. J. Fluid Mech. 464, 345–363.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 1992 Numerical Recipes in Fortran 77: The Art of Scientific Computing. Cambridge University Press.Google Scholar
Roberts, P. H. 1969 Electrohydrodynamic convection. Q. J. Mech. Appl. Maths 22, 211–220.CrossRefGoogle Scholar
Thomas, R. W. & de Vahl Davis, G. 1970 Natural convection in annular and rectangular cavities: a numerical study. In Proceedings of the 4th International Heat Transfer Conference, Paris, paper NC 2.4. Elsevier.CrossRefGoogle Scholar
Travnikov, V., Crumeyrolle, O. & Mutabazi, I. 2015 Numerical investigation of the heat transfer in cylindrical annulus with a dielectric fluid under microgravity. Phys. Fluids 27, 054103.CrossRefGoogle Scholar
Travnikov, V., Crumeyrolle, O. & Mutabazi, I. 2016 Influence of the thermo-electric coupling on the heat transfer in cylindrical annulus with a dielectric fluid under microgravity. Acta Astronaut. 129, 88–94.CrossRefGoogle Scholar
Turnbull, R. J. 1969 Effect of dielectrophoretic forces on the Bénard instability. Phys. Fluids 12, 1809–1815.CrossRefGoogle Scholar
Wadsworth, D. C. & Mudawar, I. 1990 Cooling of a multichip electronic module by means of confined two-dimensional jets of dielectric liquid. Trans. ASME J. Heat Transfer 112 (4), 891–898.CrossRefGoogle Scholar
Yavorskaya, I. M., Fomina, N. I. & Belyaev, Y. N. 1984 A simulation of central-symmetry convection in microgravity conditions. Acta Astronaut. 11, 179–183.CrossRefGoogle Scholar
Yoshikawa, H. N., Crumeyrolle, O. & Mutabazi, I. 2013 Dielectrophoretic force-driven thermal convection in annular geometry. Phys. Fluids 25, 024106.CrossRefGoogle Scholar
Yoshikawa, H. N., Meyer, A., Crumeyrolle, O. & Mutabazi, I. 2015 Linear stability of a circular Couette flow under a radial thermoelectric body force. Phys. Rev. E 91, 033003.CrossRefGoogle Scholar
Zaussinger, F., Haun, P., Neben, M., Seelig, T., Travnikov, V., Egbers, C., Yoshikawa, H. & Mutabazi, I. 2018 Dielectrically driven convection in spherical gap geometry. Phys. Rev. Fluids 3, 093501.CrossRefGoogle Scholar
Zhakin, A. I. 2012 Electrohydrodynamics. Phys. Uspekhi 55, 465–488.CrossRefGoogle Scholar

Kang and Mutabazi supplementary movie 1

See pdf file for movie caption

Download Kang and Mutabazi supplementary movie 1(Video)
Video 914.7 KB

Kang and Mutabazi supplementary movie 2

See pdf file for movie caption

Download Kang and Mutabazi supplementary movie 2(Video)
Video 1.9 MB

Kang and Mutabazi supplementary movie 3

See pdf file for movie caption

Download Kang and Mutabazi supplementary movie 3(Video)
Video 2.6 MB

Kang and Mutabazi supplementary movie 4

See pdf file for movie caption

Download Kang and Mutabazi supplementary movie 4(Video)
Video 4.4 MB

Kang and Mutabazi supplementary movie 5

See pdf file for movie caption

Download Kang and Mutabazi supplementary movie 5(Video)
Video 4.5 MB
Supplementary material: PDF

Kang and Mutabazi supplementary material

Captions for movies 1-5

Download Kang and Mutabazi supplementary material(PDF)
PDF 71.3 KB