Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-09T21:58:39.564Z Has data issue: false hasContentIssue false
  • English
  • Français

Collapse and pinch-off of a non-axisymmetric impact-created air cavity in water

Published online by Cambridge University Press:  24 April 2012

Oscar R. Enriquez ,
Ivo R. Peters ,
Stephan Gekle ,
Laura E. Schmidt ,
Detlef Lohse  and
Devaraj van der Meer
Oscar R. Enriquez*
Affiliation:
University of Twente, Enschede, 7500 AE, The Netherlands
Ivo R. Peters
Affiliation:
University of Twente, Enschede, 7500 AE, The Netherlands
Stephan Gekle
Affiliation:
University of Twente, Enschede, 7500 AE, The Netherlands
Laura E. Schmidt
Affiliation:
University of Twente, Enschede, 7500 AE, The Netherlands
Detlef Lohse
Affiliation:
University of Twente, Enschede, 7500 AE, The Netherlands
Devaraj van der Meer
Affiliation:
University of Twente, Enschede, 7500 AE, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The axisymmetric collapse of a cylindrical air cavity in water follows a universal power law with logarithmic corrections. Nonetheless, it has been suggested that the introduction of a small azimuthal disturbance induces a long-term memory effect, reflecting in oscillations which are no longer universal but remember the initial condition. In this work, we create non-axisymmetric air cavities by driving a metal disc through an initially quiescent water surface and observe their subsequent gravity-induced collapse. The cavities are characterized by azimuthal harmonic disturbances with a single mode number 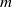and amplitude 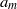. For small initial distortion amplitude (1 or 2 % of the mean disc radius), the cavity walls oscillate linearly during collapse, with nearly constant amplitude and increasing frequency. As the amplitude is increased, higher harmonics are triggered in the oscillations and we observe more complex pinch-off modes. For small-amplitude disturbances we compare our experimental results with the model for the amplitude of the oscillations by Schmidt et al. (Nature Phys., vol. 5, 2009, pp. 343–346) and the model for the collapse of an axisymmetric impact-created cavity previously proposed by Bergmann et al. (J. Fluid Mech., vol. 633, 2009b, pp. 381–409). By combining these two models we can reconstruct the three-dimensional shape of the cavity at any time before pinch-off.

JFM classification

Drops and Bubbles: Bubble dynamics Nonlinear Dynamical Systems: Pattern formation Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 701 , 25 June 2012 , pp. 40 - 58
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bergmann, R., Andersen, A., van der Meer, D. & Bohr, T. 2009a Bubble pinch-off in a rotating flow. Phys. Rev. Lett. 102 (20), 204501.CrossRefGoogle Scholar
2. Bergmann, R., van der Meer, D., Gekle, S., van der Bos, A. & Lohse, D. 2009b Controlled impact of a disk on a water surface: cavity dynamics. J. Fluid Mech. 633, 381–409.CrossRefGoogle Scholar
3. Bergmann, R., van der Meer, D., Stijnman, M., Sandtke, M., Prosperetti, A. & Lohse, D. 2006 Giant bubble pinch-off. Phys. Rev. Lett. 96 (15), 154505.CrossRefGoogle ScholarPubMed
4. Burton, J. C., Waldrep, R. & Taborek, P. 2005 Scaling and instabilities in bubble pinch-off. Phys. Rev. Lett. 94 (18), 184502.CrossRefGoogle ScholarPubMed
5. Eggers, J., Fontelos, M. A., Leppinen, D. & Snoeijer, J. H. 2007 Theory of the collapsing axisymmetric cavity. Phys. Rev. Lett. 98 (9), 094502.CrossRefGoogle ScholarPubMed
6. Enriquez, O. R., Peters, I. R., Gekle, S., Schmidt, L. E., van der Meer, D. & Lohse, D. 2011 Non-axisymmetric impact creates pineapple-shaped cavity. Phys. Fluids 23 (9), 091104.CrossRefGoogle Scholar
7. Enriquez, O. R., Peters, I. R., Gekle, S., Schmidt, L. E., van der Meer, D., Versluis, M. & Lohse, D. 2010 Collapse of non-axisymmetric cavities. Phys. Fluids 22 (9), 091104.CrossRefGoogle Scholar
8. Gekle, S., van der Bos, A., Bergmann, R., van der Meer, D. & Lohse, D. 2008 Noncontinuous froude number scaling for the closure depth of a cylindrical cavity. Phys. Rev. Lett. 100 (8), 084502.CrossRefGoogle ScholarPubMed
9. Gekle, S., Gordillo, J. M., van der Meer, D. & Lohse, D. 2009a High-speed jet formation after solid object impact. Phys. Rev. Lett. 102 (3), 034502.CrossRefGoogle ScholarPubMed
10. Gekle, S., Snoeijer, J. H., Lohse, D. & van der Meer, D. 2009b Approach to universality in axisymmetric bubble pinch-off. Phys. Rev. E 80 (3), 036305.CrossRefGoogle ScholarPubMed
11. Gordillo, J. & Perez-Saborid, M. 2006 Axisymmetric breakup of bubbles at high reynolds numbers. J. Fluid Mech 562, 303–312.CrossRefGoogle Scholar
12. Gordillo, J. M., Sevilla, A., Rodríguez-Rodríguez, J. & Martínez-Bazán, C. 2005 Axisymmetric bubble pinch-off at high Reynolds numbers. Phys. Rev. Lett. 95 (19), 194501.CrossRefGoogle ScholarPubMed
13. Grumstrup, T., Keller, J. B. & Belmonte, A. 2007 Cavity ripples observed during the impact of solid objects into liquids. Phys. Rev. Lett. 99 (11), 114502.CrossRefGoogle ScholarPubMed
14. Keim, N. C. 2011 Perturbed breakup of gas bubbles in water: Memory, gas flow, and coalescence. Phys. Rev. E 83 (5), 056325.CrossRefGoogle ScholarPubMed
15. Keim, N. C., Møller, P., Zhang, W. W. & Nagel, S. R. 2006 Breakup of air bubbles in water: Memory and breakdown of cylindrical symmetry. Phys. Rev. Lett. 97 (14), 144503.CrossRefGoogle ScholarPubMed
16. Lohse, D., Bergmann, R., Mikkelsen, R., Zeilstra, C., van der Meer, D., Versluis, M., van der Weele, K., van der Hoef, M. & Kuipers, H. 2004 Impact on soft sand: Void collapse and jet formation. Phys. Rev. Lett. 93 (19), 198003.CrossRefGoogle ScholarPubMed
17. Longuet-Higgins, M. S., Kerman, B. R. & Lunde, K. 1991 The release of air bubbles from an underwater nozzle. J. Fluid Mech. 230, 365–390.CrossRefGoogle Scholar
18. Oguz, H. N. & Prosperetti, A. 1993 Dynamics of bubble growth and detachment from a needle. J. Fluid Mech. 257, 111–145.CrossRefGoogle Scholar
19. Schmidt, L. E. 2008 Azimuthal asymmetries and vibrational modes in bubble pinch-off. PhD Thesis, University of Chicago, arXiv:1112.4440v1.Google Scholar
20. Schmidt, L. E., Keim, N. C., Zhang, W. W. & Nagel, S. R. 2009 Memory-encoding vibrations in a disconnecting air bubble. Nature Phys. 5 (5), 343–346.CrossRefGoogle Scholar
21. Thoroddsen, S. T., Etoh, T. G. & Takehara, K. 2007 Experiments on bubble pinch-off. Phys. Fluids 19 (4), 042101.CrossRefGoogle Scholar
22. Turitsyn, K. S., Lai, L. & Zhang, W. W. 2009 Asymmetric disconnection of an underwater air bubble: persistent neck vibrations evolve into a smooth contact. Phys. Rev. Lett. 103 (12), 124501.CrossRefGoogle ScholarPubMed

Enriquez et al. supplementary movie

Movie 1: Top view of collapse with m = 2 and a = 25% (Figure 3)

Download Enriquez et al. supplementary movie(Video)
Video 1.3 MB

Enriquez et al. supplementary movie

Movie 2: Top view of collapse with m = 3 and a = 10% (Figure 4)

Download Enriquez et al. supplementary movie(Video)
Video 1.1 MB

Enriquez et al. supplementary movie

Movie 3: Top view of collapse with m = 16 and a = 2% (Figure 5)

Download Enriquez et al. supplementary movie(Video)
Video 1.4 MB

Enriquez et al. supplementary movie

Movie 4: Side view of collapse with m = 20 and a = 4% (Figure 9)

Download Enriquez et al. supplementary movie(Video)
Video 1.6 MB

Enriquez et al. supplementary movie

Movie 5: Side view of collapse with m = 20 and a = 2% (Figure 10)

Download Enriquez et al. supplementary movie(Video)
Video 1.3 MB

Enriquez et al. supplementary movie

Movie 6: Top view of collapse with m = 6 and a = 4% (Figure 11a)

Download Enriquez et al. supplementary movie(Video)
Video 1.2 MB

Enriquez et al. supplementary movie

Movie 7: Top view of collapse with m = 6 and a = 10% (Figure 11b)

Download Enriquez et al. supplementary movie(Video)
Video 1.2 MB

Enriquez et al. supplementary movie

Movie 8: Top view of collapse with m = 6 and a = 25% (Figure 11c)

Download Enriquez et al. supplementary movie(Video)
Video 1.4 MB

Enriquez et al. supplementary movie

Movie 9: Top view of collapse with m = 3 and a = 25% (Figure 12)

Download Enriquez et al. supplementary movie(Video)
Video 1.3 MB

Enriquez et al. supplementary movie

Movie 10: Pinch-off comparison of a round disc and three discs with m = 6 disturbance. (Figure 13)

Download Enriquez et al. supplementary movie(Video)
Video 2.4 MB