Published online by Cambridge University Press: 21 February 2014
When a coin falls in water, its trajectory is one of four types, determined by its dimensionless moment of inertia 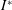 $I^\ast $ and Reynolds number
$I^\ast $ and Reynolds number 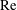 $\text {Re}$: (A) steady; (B) fluttering; (C) chaotic; or (D) tumbling. The dynamics induced by the interaction of the water with the surface of the coin, however, makes the exact landing site difficult to predict a priori. Here, we describe a carefully designed experiment in which a coin is dropped repeatedly in water to determine the probability density functions (p.d.f.s) associated with the landing positions for each of the four trajectory types, all of which are radially symmetric about the centre drop-line. In the case of the steady mode, the p.d.f. is approximately Gaussian distributed with small variances, indicating that the coin is most likely to land at the centre, right below the point from which it is dropped. For the other falling modes, the centre is one of the least likely landing sites. Indeed, the p.d.f.s of the fluttering, chaotic and tumbling modes are characterized by a ‘dip’ around the centre. In the tumbling mode, the p.d.f. is a ring configuration about the centreline whereas in the chaotic mode, the p.d.f. is generally a broadband distribution spread out radially symmetrically about the centreline. For the steady and fluttering modes, the coin never flips, so the coin lands with the same side up as when it was dropped. The probability of heads or tails is close to 0.5 for the chaotic mode and, in the case of the tumbling mode, the probability of heads or tails is based on the height of the drop which determines whether the coin flips an even or odd number of times during descent.
$\text {Re}$: (A) steady; (B) fluttering; (C) chaotic; or (D) tumbling. The dynamics induced by the interaction of the water with the surface of the coin, however, makes the exact landing site difficult to predict a priori. Here, we describe a carefully designed experiment in which a coin is dropped repeatedly in water to determine the probability density functions (p.d.f.s) associated with the landing positions for each of the four trajectory types, all of which are radially symmetric about the centre drop-line. In the case of the steady mode, the p.d.f. is approximately Gaussian distributed with small variances, indicating that the coin is most likely to land at the centre, right below the point from which it is dropped. For the other falling modes, the centre is one of the least likely landing sites. Indeed, the p.d.f.s of the fluttering, chaotic and tumbling modes are characterized by a ‘dip’ around the centre. In the tumbling mode, the p.d.f. is a ring configuration about the centreline whereas in the chaotic mode, the p.d.f. is generally a broadband distribution spread out radially symmetrically about the centreline. For the steady and fluttering modes, the coin never flips, so the coin lands with the same side up as when it was dropped. The probability of heads or tails is close to 0.5 for the chaotic mode and, in the case of the tumbling mode, the probability of heads or tails is based on the height of the drop which determines whether the coin flips an even or odd number of times during descent.
The original version of this article was published with the incorrect order of authors. A notice detailing this has been published and the error rectified in the online and print PDF and HTML copies.
Please note a has been issued for this article.