Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T08:34:00.323Z Has data issue: false hasContentIssue false
  • English
  • Français

Coherent noise sources of a subsonic round jet investigated using hydrodynamic and acoustic phased-microphone arrays

Published online by Cambridge University Press:  02 August 2013

Takao Suzuki
Takao Suzuki*
Affiliation:
Acoustics & Fluid Mechanics, The Boeing Company, Seattle, WA 98124-2207, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Based on phased-microphone array data acquired in the past, properties of coherent noise sources in a subsonic round jet are investigated at low frequencies (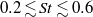$0. 2\lesssim \mathit{St}\lesssim 0. 6$) via two approaches: (i) by extracting hydrodynamic fluctuations from the near-field array, instability-wave components are projected to the acoustic field using a boundary-value problem technique; (ii) by post-processing mid-field array data in an acoustic field, noise sources are decomposed into multipole distributions using a generalized-inverse beam-forming technique. Comparison between the projected acoustic fields from the hydrodynamic array and the sound pressure levels at the acoustic array implies that the near-field pressure fluctuations beyond the end of the potential core primarily contribute to the downstream sound, as mentioned by many previous studies. However, the jet-spreading effect, which creates the streamwise growth and decay of the eigenfunctions in linear stability analysis, is insufficient to generate the sound pressure levels measured in the acoustic array. In the actual hydrodynamic data, the streamwise decay is much slower and the phase velocity is faster than those of the corresponding eigenfunction beyond the peak of the wave-packet, and these factors govern the downstream sound. Results from the acoustic array demonstrate that free-space multipole distributions detected by generalized-inverse beam-forming can reproduce primary coherent modes, the first one predominantly propagating downstream and the second one typically being more omni-directional. In particular, the detected phase relation of the first coherent mode shows nearly a constant slope, indicating a wavy-type source structure and the relation of downstream sound with instability waves.

JFM classification

Acoustics: Acoustics Acoustics: Aeroacoustics Acoustics: Jet noise
Type
Papers
Information
Journal of Fluid Mechanics , Volume 730 , 10 September 2013 , pp. 659 - 698
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahuja, K. K. 1973 Correlation and prediction of jet noise. J. Sound Vib. 29 (2), 155–168.Google Scholar
Armstrong, R. R. 1981 Influence on Mach number on coherent structure relevant to jet noise. AIAA J. 19 (6), 677–683.Google Scholar
Arndt, R. E. A., Long, D. F. & Glauser, M. N. 1997 The proper orthogonal decomposition of pressure fluctuations surrounding a turbulent jet. J. Fluid Mech. 340, 1–33.Google Scholar
Blokhintzev, D. I. 1946 The propagation of sound in an inhomogeneous and moving medium. Part 1. J. Acoust. Soc. Am. 18 (2), 322–328.Google Scholar
Boyd, J. P. 1985 Complex coordinate methods for hydrodynamic instabilities and Sturm–Liouville eigenproblems with an interior singularity. J. Comput. Phys. 57, 454–471.CrossRefGoogle Scholar
Bridges, J. & Brown, C. 2005 Validation of the small hot jet acoustic rig for aeroacoustic research. AIAA Paper 2005-2846.CrossRefGoogle Scholar
Bridges, J., Khavaran, A. & Hunter, C. A. 2008 Assessment of current jet noise prediction capabilities. AIAA Paper 2008-2933.Google Scholar
Bridges, J. & Wernet, M. 2003 Measurements of the aeroacoustic sound source in hot jets. AIAA Paper 2003–3130.Google Scholar
Cavalieri, A. V. G., Jordan, P., Agarwal, A. & Gervais, Y. 2011 Jittering wave-packet models for subsonic jet noise. J. Sound Vib. 330, 4474–4492.Google Scholar
Citriniti, J. H. & George, W. K. 2000 Reconstruction of the global velocity field in the axisymmetric mixing layer utilizing the proper orthogonal decomposition. J. Fluid Mech. 418, 137–166.Google Scholar
Colonius, T., Lele, S. K. & Moin, P. 1997 Sound generated in a mixing layer. J. Fluid Mech. 330, 375–409.Google Scholar
Crighton, D. G. 1975 Basic principles of aerodynamic noise generation. Prog. Aerosp. Sci. 16, 31–96.Google Scholar
Crighton, D. G. & Huerre, P. 1990 Shear-layer pressure fluctuations and superdirective acoustic sources. J. Fluid Mech. 220, 355–368.CrossRefGoogle Scholar
Crow, S. C. & Champagne, F. H. 1971 Orderly structure in jet turbulence. J. Fluid Mech. 48, 547–591.Google Scholar
Dougherty, R. P. 2012 Improved generalized inverse beamforming for jet noise. Intl J. Aeroacoust. 11 (3–4), 259–290.CrossRefGoogle Scholar
Dowling, A. P., Ffowcs Williams, J. E. & Goldstein, M. E. 1978 Sound production in a moving stream. Phil. Trans. R. Soc. Lond. A 288, 321–349.Google Scholar
Durbin, P. A. 1983 High frequency Green function for aerodynamic noise in moving media. Part 1. General theory. J. Sound Vib. 91 (4), 519–525.CrossRefGoogle Scholar
Faranosov, G. A. & Kopiev, V. F. 2009 Localization of sound sources by means of ADT data interpretation improved by refraction effect consideration. AIAA Paper 2009-3215.Google Scholar
Ffowcs Williams, J. E. 1963 The noise from turbulence convected at high speed. Phil. Trans. R. Soc. Lond. A 254, 469–503.Google Scholar
Ffowcs Williams, J. E. & Kempton, A. J. 1978 The noise from the large-scale structure of a jet. J. Fluid Mech. 84, 673–694.Google Scholar
Goldstein, M. E. 1976 Aeroacoustics. McGraw-Hill.Google Scholar
Goldstein, M. E. 1982 High frequency sound emission from moving point multipole sources embedded in arbitrary transversely sheared mean flows. J. Sound Vib. 80 (4), 499–522.Google Scholar
Goldstein, M. E. 2003 A generalized acoustic analogy. J. Fluid Mech. 488, 315–333.CrossRefGoogle Scholar
Goldstein, M. E. 2011 Recent developments in the application of the generalized acoustic analogy to jet noise prediction. Intl J. Aeroacoust. 10 (2–3), 89–116.Google Scholar
Goldstein, M. E. & Leib, S. J. 2005 The role of instability waves in predicting jet noise. J. Fluid Mech. 525, 37–72.CrossRefGoogle Scholar
Gudmundsson, K. & Colonius, T. 2011 Instability wave models for the near-field fluctuations of turbulent jets. J. Fluid Mech. 689, 97–128.Google Scholar
Hileman, J. I., Thurow, B. S., Caraballo, E. J. & Samimy, M. 2005 Large-scale structure evolution and sound emission in high-speed jets: real-time visualization with simultaneous acoustic measurements. J. Fluid Mech. 544, 277–307.Google Scholar
Howe, M. S. 1970 Transmission of an acoustic pulse through a plane vortex sheet. J. Fluid Mech. 43, 353–367.Google Scholar
Howe, M. S. 1975 Contributions to the theory of aerodynamic sound, with application to excess jet noise and the theory of the flute. J. Fluid Mech. 71, 625–673.Google Scholar
Huber, P. J. 1981 Robust Statistics. Wiley.Google Scholar
Jordan, P. & Colonius, T. 2013 Wave packets and turbulent jet noise. Annu. Rev. Fluid Mech. 45, 173–195.Google Scholar
Jordan, P. & Gervais, Y. 2008 Subsonic jet aeroacoustics: associating experiment, modelling and simulation. Exp. Fluids 44 (1), 1–21.Google Scholar
Laufer, J., Schlinker, R. H. & Kaplan, R. E. 1976 Experiments on supersonic jet noise. AIAA J. 14 (4), 489–497.CrossRefGoogle Scholar
Lee, M. & Bolton, J. S. 2007 Source characterization of a subsonic jet by using near-field acoustical holography. J. Acoust. Soc. Am. 121 (2), 967–977.Google Scholar
Lee, S.-S. & Bridges, J. 2005 Phased-array measurements of single flow hot jets. AIAA Paper 2005-2842.CrossRefGoogle Scholar
Leib, S. J. & Goldstein, M. E. 2011 Hybrid source model for predicting high-speed jet noise. AIAA J. 49 (7), 1324–1335.Google Scholar
Lighthill, M. J. 1952 On sound generated aerodynamically. Part 1. General theory. Proc. R. Soc. Lond. A 211, 564–587.Google Scholar
Lighthill, M. J. 1954 On sound generated aerodynamically. Part 2. Turbulence as a source of sound. Proc. R. Soc. Lond. A 222, 1–32.Google Scholar
Lilley, G. M. 1974 On the noise from jets. AGARD-CP-131.Google Scholar
Maestrello, L. & Fung, Y.-T. 1979 Quasi-periodic structure of a turbulent jet. J. Sound Vib. 64 (1), 107–122.CrossRefGoogle Scholar
Mani, R. 1976 The influence of jet flow on jet noise. Part 1. The noise of unheated jets. J. Fluid Mech. 73, 753–778.Google Scholar
Mankbadi, R. R. & Liu, J. T. C. 1984 Sound generated aerodynamically revisited: large-scale coherent structures in a turbulent jet as a source of sound. Proc. R. Soc. Lond. A 311, 183–217.Google Scholar
Michalke, A. & Fuchs, H. V. 1975 On turbulence and noise of an axisymmetric shear flow. J. Fluid Mech. 70, 179–205.Google Scholar
Morris, P. J. & Farassat, F. 2002 Acoustic analogy and alternative theories for jet noise prediction. AIAA J. 40 (4), 671–680.Google Scholar
Oestreicher, H. L. 1957 Representation of the field of an acoustic source as a series of multipole fields. J. Acoust. Soc. Am. 29 (11), 1219–1222.Google Scholar
Phillips, O. M. 1960 On the generation of sound by supersonic turbulent shear layers. J. Fluid Mech. 9, 1–28.Google Scholar
Pridmore-Brown, D. C. 1958 Sound propagation in a fluid flowing through an attenuating duct. J. Fluid Mech. 4, 399–406.Google Scholar
Reba, R. A., Narayanan, S., Colonius, T. & Suzuki, T. 2005 Modeling jet noise from organized structures using near-field hydrodynamic pressure. AIAA Paper 2005-3093.Google Scholar
Reba, R. A., Simonich, J. C. & Schlinker, R. H. 2008 Measurement of source wave-packets in high-speed jets and connection to far-field sound. AIAA Paper 2008-2891.Google Scholar
Schlichting, H. 1960 Boundary-Layer Theory. McGraw-Hill.Google Scholar
Suponitsky, V., Sandham, N. D. & Morfey, C. L. 2010 Linear and nonlinear mechanisms of sound radiation by instability waves in subsonic jets. J. Fluid Mech. 658, 509–538.Google Scholar
Suzuki, T. 2006 Identification of multipole noise sources in low Mach number jets near the peak frequency. J. Acoust. Soc. Am. 119 (6), 3649–3659.Google Scholar
Suzuki, T. 2010 Review of diagnostic studies on jet-noise sources and generation mechanisms of subsonically-convecting jets. Fluid Dyn. Res. 42, 014001.Google Scholar
Suzuki, T. 2011 ${L}_{1} $ generalized inverse beam-forming algorithm resolving coherent/incoherent, distributed and multipole sources. J. Sound Vib. 330 (24), 5835–5851.Google Scholar
Suzuki, T. & Colonius, T. 2006 Instability waves in a subsonic round jet detected using a near-field phased microphone array. J. Fluid Mech. 565, 197–226.CrossRefGoogle Scholar
Suzuki, T. & Lele, S. K. 2002 Refracted arrival waves in a zone of silence from a finite thickness mixing layer. J. Acoust. Soc. Am. 111 (2), 716–728.Google Scholar
Suzuki, T. & Lele, S. K. 2003 Green’s functions for a source in a mixing layer: direct waves, refracted arrival waves and instability waves. J. Fluid Mech. 477, 89–128.Google Scholar
Tam, C. K. W. & Auriault, L. 1999 Jet mixing noise from fine-scale turbulence. AIAA J. 37 (2), 145–153.CrossRefGoogle Scholar
Tam, C. K. W., Golebiowski, M. & Seiner, J. M. 1996 Two components of turbulent mixing noise from supersonic jets. AIAA Paper 1996-1716.CrossRefGoogle Scholar
Tam, C. K. W. & Morris, P. J. 1980 The radiation of sound by the instability waves of a compressible plane turbulent shear layer. J. Fluid Mech. 98, 349–381.Google Scholar
Tam, C. K. W., Viswanathan, K., Ahuja, K. K. & Panda, J. 2008 The sources of jet noise: experimental evidence. J. Fluid Mech. 615, 253–292.Google Scholar
Tanna, H. K. 1977 An experimental study of jet noise. Part 1. Turbulent mixing noise. J. Sound Vib. 50 (3), 405–428.Google Scholar
Tester, B. J. & Glegg, S. A. L. 2008 A review of engine noise source diagnostic methods for static engine tests, with phased arrays and polar correlation techniques. AIAA Paper 2008-2854.Google Scholar
Tester, B. J. & Morfey, C. L. 1976 Developments in jet noise modelling: theoretical predictions and comparisons with measured data. J. Sound Vib. 46 (1), 79–103.Google Scholar
Tinney, C. E., Ukeiley, L. S. & Glauser, M. N. 2008 Low-dimensional characteristics of a transonic jet. Part 2. Estimate and far-field prediction. J. Fluid Mech. 615, 53–92.CrossRefGoogle Scholar
Ukeiley, L. S. & Ponton, M. K. 2004 On the near field pressure of a transonic axisymmetric jet. Intl J. Aeroacoust. 3 (1), 43–65.Google Scholar
Venkatesh, S. R., Polak, D. R. & Narayanan, S. 2003 Beamforming algorithm for distributed source localization and its application to jet noise. AIAA J. 41 (7), 1238–1246.Google Scholar
Viswanathan, K. 2004 Aeroacoustics of hot jets. J. Fluid Mech. 516, 39–82.Google Scholar
Wundrow, D. W. & Khavaran, A. 2004 On the applicability of high-frequency approximations to Lilley’s equation. J. Sound Vib. 272 (3–5), 793–830.Google Scholar