Article contents
Coalescence of drops with mobile interfaces in a quiescent fluid
Published online by Cambridge University Press: 11 July 2013
Abstract
A study on the axisymmetric near-contact motion of drops with tangentially mobile interfaces under the action of a body force in a quiescent fluid is described. A long-time asymptotic analysis is presented for small-deformation conditions. Under these conditions the drops are nearly spherical, except in the near-contact region, where a flattened thin film forms. According to our analysis, a hydrostatic dome does not form in the near-contact region at long times, in contrast to the assumption underlying all previous analyses of this problem. Instead, the shape of the film in the near-contact region results from the absence of tangential stresses acting on it. As a result, the long-time behaviour of the system is qualitatively different than previously predicted. According to the theory presented herein, the minimum film thickness (rim region) decays with time as 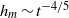 ${h}_{m} \sim {t}^{- 4/ 5} $, and the thickness at the centre of the film decays as
${h}_{m} \sim {t}^{- 4/ 5} $, and the thickness at the centre of the film decays as 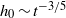 ${h}_{0} \sim {t}^{- 3/ 5} $, which is a faster decay than predicted by prior analyses based on a hydrostatic dome. Numerical thin-film simulations quantitatively confirm the predictions of our small-deformation theory. Boundary-integral simulations of the full two-drop problem suggest that the theory also describes qualitatively the long-time evolution under finite-deformation conditions.
${h}_{0} \sim {t}^{- 3/ 5} $, which is a faster decay than predicted by prior analyses based on a hydrostatic dome. Numerical thin-film simulations quantitatively confirm the predictions of our small-deformation theory. Boundary-integral simulations of the full two-drop problem suggest that the theory also describes qualitatively the long-time evolution under finite-deformation conditions.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 10
- Cited by


