Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-03T00:42:14.209Z Has data issue: false hasContentIssue false
  • English
  • Français

Coalescence and break-up of nearly inviscid conical droplets

Published online by Cambridge University Press:  17 December 2014

Casey T. Bartlett ,
Guillaume A. Généro  and
James C. Bird
Casey T. Bartlett
Affiliation:
Department of Mechanical Engineering, Boston University, Boston, MA 02215, USA
Guillaume A. Généro
Affiliation:
Department of Mechanical Engineering, Boston University, Boston, MA 02215, USA École Polytechnique, Route de Saclay, 91128 Palaiseau, France
James C. Bird*
Affiliation:
Department of Mechanical Engineering, Boston University, Boston, MA 02215, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the presence of electric fields, pairs of liquid drops can be rapidly drawn together such that, at contact, the deformed interface resembles a double-cone. Following contact, these drop pairs are observed to either coalesce or recoil. Experimental and theoretical results suggest that the transition between coalescence and recoil is due to the conical drop topology rather than charge effects. However, even with this assumption, existing models disagree on how the transition develops, leading to different predictions of the critical cone angle and bridge morphology. Here we use high-resolution numerical simulations to highlight the impact of the initial double-cone angle on drop coalescence and reconcile the differences in the previous models. The results demonstrate a self-similar behaviour at intermediate scales for both coalescence and recoil that is independent of the other length scales in the problem. 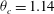We calculate a critical polar angle of ${\it\theta}_{c}=1.14$ rad (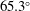$65.3^{\circ }$), or a complementary angle of 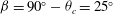${\it\beta}=90^{\circ }-{\it\theta}_{c}=25^{\circ }$. This calculated critical angle for morphological transition is in agreement with previous experimental observations of 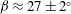${\it\beta}\approx 27\pm 2^{\circ }$.

JFM classification

Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Drops and Bubbles Interfacial Flows (free surface): Liquid bridges
Type
Papers
Information
Journal of Fluid Mechanics , Volume 763 , 25 January 2015 , pp. 369 - 385
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barenblatt, G. I. & Zel’Dovich, Y. B. 1972 Self-similar solutions as intermediate asymptotics. Annu. Rev. Fluid Mech. 4 (1), 285–312.Google Scholar
Billingham, J. 1999 Surface-tension-driven flow in fat fluid wedges and cones. J. Fluid Mech. 397, 45–71.Google Scholar
Billingham, J. & King, A. C. 2005 Surface-tension-driven flow outside a slender wedge with an application to the inviscid coalescence of drops. J. Fluid Mech. 533, 193–221.Google Scholar
Bird, J. C., Ristenpart, W. D., Belmonte, A. & Stone, H. A. 2009 Critical angle for electrically driven coalescence of two conical droplets. Phys. Rev. Lett. 103 (16), 164502.Google Scholar
Bremond, N., Thiam, A. R. & Bibette, J. 2008 Decompressing emulsion droplets favors coalescence. Phys. Rev. Lett. 100 (2), 024501.Google Scholar
Brenner, M. P., Eggers, J., Joseph, K., Nagel, S. R. & Shi, X. D. 1997 Breakdown of scaling in droplet fission at high Reynolds number. Phys. Fluids 9, 1573–1590.CrossRefGoogle Scholar
Burton, J. C. & Taborek, P. 2007 Two-dimensional inviscid pinch-off: an example of self-similarity of the second kind. Phys. Fluids 19 (10), 102109.Google Scholar
Chen, G., Tan, P., Chen, S., Huang, J., Wen, W. & Xu, L. 2013 Coalescence of pickering emulsion droplets induced by an electric field. Phys. Rev. Lett. 110 (6), 064502.Google Scholar
Day, R. F., Hinch, E. J. & Lister, J. R. 1998 Self-similar capillary pinchoff of an inviscid fluid. Phys. Rev. Lett. 80 (4), 704–707.Google Scholar
Duchemin, L., Eggers, J. & Josserand, C. 2003 Inviscid coalescence of drops. J. Fluid Mech. 487, 167–178.Google Scholar
Eggers, J. 1997 Nonlinear dynamics and breakup of free-surface flows. Rev. Mod. Phys. 69 (3), 865–929.Google Scholar
Eggers, J., Lister, J. R. & Stone, H. A. 1999 Coalescence of liquid drops. J. Fluid Mech. 401, 293–310.Google Scholar
Eow, J. S., Ghadiri, M., Sharif, A. O. & Williams, T. J. 2001 Electrostatic enhancement of coalescence of water droplets in oil: a review of the current understanding. Chem. Engng J. 84 (3), 173–192.Google Scholar
de Gennes, P. G., Brochard-Wyart, F. & Quere, D. 2004 Capillarity and Wetting Phenomena. Springer.Google Scholar
Helmensdorfer, S. 2012 A model for the behavior of fluid droplets based on mean curvature flow. SIAM J. Math. Anal. 44 (3), 1359–1371.Google Scholar
Helmensdorfer, S. & Topping, P. 2013 Bouncing of charged droplets: an explanation using mean curvature flow. Eur. Phys. Lett. 104 (3), 34001.Google Scholar
Keller, J. B. & Miksis, M. J. 1983 Surface tension driven flows. SIAM J. Appl. Maths 43 (2), 268–277.CrossRefGoogle Scholar
Keller, J. B., Milewski, P. A. & Vanden-Broeck, J. M. 2000 Merging and wetting driven by surface tension. Eur. J. Mech. (B/Fluids) 19 (4), 491–502.Google Scholar
Latham, J. 1969 Cloud physics. Rep. Prog. Phys. 32 (1), 69–134.Google Scholar
Lawrie, J. B. 1990 Surface-tension-driven flow in a wedge. Q. J. Mech. Appl. Maths 43 (2), 251–273.CrossRefGoogle Scholar
Leppinen, D. & Lister, J. R. 2003 Capillary pinch-off in inviscid fluids. Phys. Fluids 15, 568–578.Google Scholar
Liu, T., Seiffert, S., Thiele, J., Abate, A. R., Weitz, D. A. & Richtering, W. 2012 Non-coalescence of oppositely charged droplets in ph-sensitive emulsions. Proc. Natl Acad. Sci. USA 109 (2), 384–389.Google Scholar
de la Mora, J. F. 2007 The fluid dynamics of Taylor cones. Annu. Rev. Fluid Mech. 39, 217–243.Google Scholar
Peregrine, D. H., Shoker, G. & Symon, A. 1990 The bifurcation of liquid bridges. J. Fluid Mech. 212, 25–39.Google Scholar
Popinet, S. 2003 Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries. J. Comput. Phys. 190 (2), 572–600.CrossRefGoogle Scholar
Ristenpart, W. D., Bird, J. C., Belmonte, A., Dollar, F. & Stone, H. A. 2009 Non-coalescence of oppositely charged drops. Nature 461 (7262), 377–380.Google Scholar
Shi, X. D., Brenner, M. P. & Nagel, S. R. 1994 A cascade of structure in a drop falling from a faucet. Science 265 (5169), 219–222.CrossRefGoogle Scholar
Sierou, A. & Lister, J. R. 2004 Self-similar recoil of inviscid drops. Phys. Fluids 16, 1379–1394.Google Scholar
Taylor, G. 1964 Disintegration of water drops in electric field. Proc. R. Soc. Lond. A 280 (138), 383–397.Google Scholar
Thiam, A. R., Bremond, N. & Bibette, J. 2009 Breaking of an emulsion under an ac electric field. Phys. Rev. Lett. 102 (18), 188304.Google Scholar
Thoraval, M., Takehara, K., Etoh, T. G., Popinet, S., Ray, P., Josserand, C., Zaleski, S. & Thoroddsen, S. T. 2012 von Kármán vortex street within an impacting drop. Phys. Rev. Lett. 108, 264506.Google Scholar
Thoroddsen, S. T., Takehara, K. & Etoh, T. G. 2005 The coalescence speed of a pendent and a sessile drop. J. Fluid Mech. 527, 85–114.Google Scholar
Wu, M. M., Cubaud, T. & Ho, C. M. 2004 Scaling law in liquid drop coalescence driven by surface tension. Phys. Fluids 16 (7), L51–L54.CrossRefGoogle Scholar
Yoon, Y., Baldessari, F., Ceniceros, H. D. & Leal, L. G. 2007 Coalescence of two equal-sized deformable drops in an axisymmetric flow. Phys. Fluids 19, 102102.CrossRefGoogle Scholar