Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-17T05:17:15.313Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterization of velocity-gradient dynamics in incompressible turbulence using local streamline geometry

Published online by Cambridge University Press:  15 May 2020

Rishita Das Open the ORCID record for Rishita Das [Opens in a new window]  and
Sharath S. Girimaji
Rishita Das*
Affiliation:
Department of Aerospace Engineering, Texas A&M University, College Station, TX77843, USA
Sharath S. Girimaji
Affiliation:
Department of Ocean Engineering, Texas A&M University, College Station, TX77843, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This study develops a comprehensive description of local streamline geometry and uses the resulting shape features to characterize velocity gradient ($\unicode[STIX]{x1D608}_{ij}=\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}$) dynamics. The local streamline geometric shape parameters and scale factor (size) are extracted from $\unicode[STIX]{x1D608}_{ij}$ by extending the linearized critical point analysis. In the present analysis, $\unicode[STIX]{x1D608}_{ij}$ is factorized into its magnitude ($A\equiv \sqrt{\unicode[STIX]{x1D608}_{ij}\unicode[STIX]{x1D608}_{ij}}$) and normalized tensor $\unicode[STIX]{x1D623}_{ij}\equiv \unicode[STIX]{x1D608}_{ij}/A$. The geometric shape is shown to be determined exclusively by four $\unicode[STIX]{x1D623}_{ij}$ parameters: second invariant, $q$ ($=Q/A^{2}$); third invariant, $r$ ($=R/A^{3}$); intermediate strain rate eigenvalue, $a_{2}$; and vorticity component along intermediate strain rate eigenvector, $\unicode[STIX]{x1D714}_{2}$. 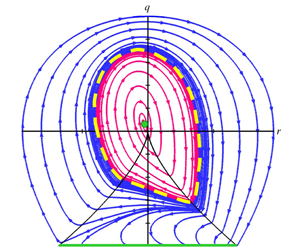Velocity gradient magnitude, $A$, plays a role only in determining the scale of the local streamline structure. Direct numerical simulation data of forced isotropic turbulence ($Re_{\unicode[STIX]{x1D706}}\sim 200{-}600$) is used to establish streamline shape and scale distribution, and then to characterize velocity-gradient dynamics. Conditional mean trajectories (CMTs) in $q$–$r$ space reveal important non-local features of pressure and viscous dynamics which are not evident from the $\unicode[STIX]{x1D608}_{ij}$-invariants. Two distinct types of $q$–$r$ CMTs demarcated by a separatrix are identified. The inner trajectories are dominated by inertia–pressure interactions and the viscous effects play a significant role only in the outer trajectories. Dynamical system characterization of inertial, pressure and viscous effects in the $q$–$r$ phase space is developed. Additionally, it is shown that the residence time of $q$–$r$ CMTs through different topologies correlate well with the corresponding population fractions. These findings not only lead to improved understanding of non-local dynamics, but also provide an important foundation for developing Lagrangian velocity-gradient models.

JFM classification

Turbulent Flows: Turbulence theory Turbulent Flows: Isotropic turbulence Turbulent Flows: Intermittency
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 895 , 25 July 2020 , A5
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashurst, W. T., Kerstein, A. R., Kerr, R. M. & Gibson, C. H. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30 (8), 2343–2353.CrossRefGoogle Scholar
Atkinson, C., Chumakov, S., Bermejo-Moreno, I. & Soria, J. 2012 Lagrangian evolution of the invariants of the velocity gradient tensor in a turbulent boundary layer. Phys. Fluids 24 (10), 871–884.CrossRefGoogle Scholar
Bechlars, P. & Sandberg, R. D. 2017 Evolution of the velocity gradient tensor invariant dynamics in a turbulent boundary layer. J. Fluid Mech. 815, 223–242.CrossRefGoogle Scholar
Bikkani, R. K. & Girimaji, S. S. 2007 Role of pressure in nonlinear velocity gradient dynamics in turbulence. Phys. Rev. E 75 (3), 036307.Google ScholarPubMed
Blackburn, H. M., Mansour, N. N. & Cantwell, B. J. 1996 Topology of fine-scale motions in turbulent channel flow. J. Fluid Mech. 310, 269–292.CrossRefGoogle Scholar
Blackett, D. W. 2014 Elementary Topology: A Combinatorial and Algebraic Approach. Elsevier.Google Scholar
Blaisdell, G. A. & Shariff, K. 1996 Simulation and modeling of the elliptic streamline flow. In Studying Turbulence Using Numerical Simulation Databases, Part 6; NASA-TM-111953, pp. 433–446.Google Scholar
Buaria, D., Pumir, A., Bodenschatz, E. & Yeung, P.-K. 2019 Extreme velocity gradients in turbulent flows. New J. Phys 21 (4), 043004.CrossRefGoogle Scholar
Cantwell, B. J. 1992 Exact solution of a restricted Euler equation for the velocity gradient tensor. Phys. Fluids A 4 (4), 782–793.CrossRefGoogle Scholar
Chacin, J. M. & Cantwell, B. J. 2000 Dynamics of a low Reynolds number turbulent boundary layer. J. Fluid Mech. 404, 87–115.CrossRefGoogle Scholar
Chacín, J. M., Cantwell, B. J. & Kline, S. J. 1996 Study of turbulent boundary layer structure using the invariants of the velocity gradient tensor. Exp. Therm. Fluid Sci. 13 (4), 308–317.CrossRefGoogle Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.CrossRefGoogle Scholar
Chertkov, M., Pumir, A. & Shraiman, B. I. 1999 Lagrangian tetrad dynamics and the phenomenology of turbulence. Phys. Fluids 11 (8), 2394–2410.CrossRefGoogle Scholar
Chevillard, L. & Meneveau, C. 2006 Lagrangian dynamics and statistical geometric structure of turbulence. Phys. Rev. Lett. 97 (17), 174501.CrossRefGoogle ScholarPubMed
Chevillard, L., Meneveau, C., Biferale, L. & Toschi, F. 2008 Modeling the pressure Hessian and viscous Laplacian in turbulence: comparisons with direct numerical simulation and implications on velocity gradient dynamics. Phys. Fluids 20 (10), 101504.CrossRefGoogle Scholar
Chong, M. S., Soria, J., Perry, A. E., Chacin, J., Cantwell, B. J. & Na, Y. 1998 Turbulence structures of wall-bounded shear flows found using DNS data. J. Fluid Mech. 357, 225–247.CrossRefGoogle Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2 (5), 765–777.CrossRefGoogle Scholar
Danish, M. & Meneveau, C. 2018 Multiscale analysis of the invariants of the velocity gradient tensor in isotropic turbulence. Phys. Rev. Fluids 3 (4), 044604.CrossRefGoogle Scholar
Das, R. & Girimaji, S. S. 2019 On the Reynolds number dependence of velocity-gradient structure and dynamics. J. Fluid Mech. 861, 163–179.CrossRefGoogle Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2012 Some results on the Reynolds number scaling of pressure statistics in isotropic turbulence. Phys. D 241 (3), 164–168.Google Scholar
Donzis, D. A., Yeung, P. K. & Sreenivasan, K. R. 2008 Dissipation and enstrophy in isotropic turbulence: resolution effects and scaling in direct numerical simulations. Phys. Fluids 20 (4), 045108.CrossRefGoogle Scholar
Donzis, D. A. & Sreenivasan, K. R. 2010 Short-term forecasts and scaling of intense events in turbulence. J. Fluid Mech. 647, 13–26.CrossRefGoogle Scholar
Dresselhaus, E. & Tabor, M. 1992 The kinematics of stretching and alignment of material elements in general flow fields. J. Fluid Mech. 236, 415–444.CrossRefGoogle Scholar
Elsinga, G. E. & Marusic, I. 2010a Evolution and lifetimes of flow topology in a turbulent boundary layer. Phys. Fluids 22 (1), 015102.CrossRefGoogle Scholar
Elsinga, G. E. & Marusic, I. 2010b Universal aspects of small-scale motions in turbulence. J. Fluid Mech. 662, 514–539.CrossRefGoogle Scholar
Gibbon, J. D., Donzis, D. A., Gupta, A., Kerr, R. M., Pandit, R. & Vincenzi, D. 2014 Regimes of nonlinear depletion and regularity in the 3D Navier–Stokes equations. Nonlinearity 27 (10), 2605–2625.CrossRefGoogle Scholar
Girimaji, S. S. & Pope, S. B. 1990a A diffusion model for velocity gradients in turbulence. Phys. Fluids A 2 (2), 242–256.CrossRefGoogle Scholar
Girimaji, S. S. & Pope, S. B. 1990b Material-element deformation in isotropic turbulence. J. Fluid Mech. 220, 427–458.CrossRefGoogle Scholar
Girimaji, S. S. & Speziale, C. G. 1995 A modified restricted Euler equation for turbulent flows with mean velocity gradients. Phys. Fluids 7 (6), 1438–1446.CrossRefGoogle Scholar
Hamlington, P. E., Schumacher, J. & Dahm, W. J. 2008 Direct assessment of vorticity alignment with local and nonlocal strain rates in turbulent flows. Phys. Fluids 20 (11), 111703.CrossRefGoogle Scholar
Jeong, E. & Girimaji, S. S. 2003 Velocity-gradient dynamics in turbulence: effect of viscosity and forcing. Theoret. Comput. Fluid Dyn. 16 (6), 421–432.CrossRefGoogle Scholar
Johnson, P. L. & Meneveau, C. 2016 A closure for Lagrangian velocity gradient evolution in turbulence using recent-deformation mapping of initially Gaussian fields. J. Fluid Mech. 804, 387–419.CrossRefGoogle Scholar
Kaplan, W. 1958 Ordinary Differential Equations. Addison-Wesley.Google Scholar
Kerr, R. M. 1987 Histograms of helicity and strain in numerical turbulence. Phys. Rev. Lett. 59 (7), 783–786.CrossRefGoogle ScholarPubMed
Keylock, C. J. 2018 The Schur decomposition of the velocity gradient tensor for turbulent flows. J. Fluid Mech. 848, 876–905.CrossRefGoogle Scholar
Kinsey, L. C. 1993 Topology of Surfaces. Springer.CrossRefGoogle Scholar
Martín, J., Dopazo, C. & Valiño, L. 1998a Dynamics of velocity gradient invariants in turbulence: restricted Euler and linear diffusion models. Phys. Fluids 10 (8), 2012–2025.CrossRefGoogle Scholar
Martín, J., Ooi, A., Chong, M. S. & Soria, J. 1998b Dynamics of the velocity gradient tensor invariants in isotropic turbulence. Phys. Fluids 10 (9), 2336–2346.CrossRefGoogle Scholar
Monin, A. S. & Yaglom, A. M. 2013 Statistical Fluid Mechanics, Volume II: Mechanics of Turbulence. Dover.Google Scholar
Nomura, K. K. & Post, G. K. 1998 The structure and dynamics of vorticity and rate of strain in incompressible homogeneous turbulence. J. Fluid Mech. 377, 65–97.CrossRefGoogle Scholar
Ooi, A., Martín, J., Soria, J. & Chong, M. S. 1999 A study of the evolution and characteristics of the invariants of the velocity-gradient tensor in isotropic turbulence. J. Fluid Mech. 381, 141–174.CrossRefGoogle Scholar
Orszag, S. A. 1970 Comments on ‘Turbulent hydrodynamic line stretching: consequences of isotropy’. Phys. Fluids 13 (8), 2203–2204.CrossRefGoogle Scholar
Parashar, N., Sinha, S. S. & Srinivasan, B. 2019 Lagrangian investigations of velocity gradients in compressible turbulence: lifetime of flow-field topologies. J. Fluid Mech. 872, 492–514.CrossRefGoogle Scholar
Perry, A. E. & Chong, M. S. 1994 Topology of flow patterns in vortex motions and turbulence. Appl. Sci. Res. 53 (3–4), 357–374.CrossRefGoogle Scholar
Perry, A. E. & Fairlie, B. D. 1975 Critical points in flow patterns. In Advances in Geophysics, vol. 18, pp. 299–315. Elsevier.Google Scholar
Perry, A. E. & Chong, M. S. 1987 A description of eddying motions and flow patterns using critical-point concepts. Annu. Rev. Fluid Mech. 19 (1), 125–155.CrossRefGoogle Scholar
Smart, J. R. 1998 Modern Geometries, A Gary W. Ostedt book 9780534351885. Brooks/Cole.Google Scholar
Soria, J., Sondergaard, R., Cantwell, B. J., Chong, M. S. & Perry, A. E. 1994 A study of the fine-scale motions of incompressible time-developing mixing layers. Phys. Fluids 6 (2), 871–884.CrossRefGoogle Scholar
Vieillefosse, P. 1984 Internal motion of a small element of fluid in an inviscid flow. Phys. A 125 (1), 150–162.Google Scholar
Wang, X., Szalay, A., Aragón-Calvo, M. A., Neyrinck, M. C. & Eyink, G. L. 2014 Kinematic morphology of large-scale structure: evolution from potential to rotational flow. Astrophys. J. 793 (1), 58.CrossRefGoogle Scholar
Yale, P. B. 1968 Geometry and Symmetry, Dover Books on Mathematics Series 9780486657790. Dover.Google Scholar
Yeung, P. K., Sreenivasan, K. R. & Pope, S. B. 2018 Effects of finite spatial and temporal resolution in direct numerical simulations of incompressible isotropic turbulence. Phys. Rev. Fluids 3 (6), 064603.CrossRefGoogle Scholar