Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kuwata, Y.
Tsuda, K.
and
Suga, K.
2020.
Direct numerical simulation of turbulent conjugate heat transfer in a porous-walled duct flow.
Journal of Fluid Mechanics,
Vol. 904,
Issue. ,
Chavarin, Andrew
Efstathiou, Christoph
Vijay, Shilpa
and
Luhar, Mitul
2020.
Resolvent-based design and experimental testing of porous materials for passive turbulence control.
International Journal of Heat and Fluid Flow,
Vol. 86,
Issue. ,
p.
108722.
Wang, Wenkang
Chu, Xu
Lozano-Durán, Adrián
Helmig, Rainer
and
Weigand, Bernhard
2021.
Information transfer between turbulent boundary layers and porous media.
Journal of Fluid Mechanics,
Vol. 920,
Issue. ,
Wang, Wenkang
Yang, Guang
Evrim, Cenk
Terzis, Alexandros
Helmig, Rainer
and
Chu, Xu
2021.
An assessment of turbulence transportation near regular and random permeable interfaces.
Physics of Fluids,
Vol. 33,
Issue. 11,
OKAZAKI, Yuki
TAKASE, Yumeto
KUWATA, Yusuke
and
SUGA, Kazuhiko
2021.
Describing characteristic parameters of turbulence over two-dimensional porous roughness.
Journal of Thermal Science and Technology,
Vol. 16,
Issue. 2,
p.
JTST0027.
Chu, Xu
Wang, Wenkang
Yang, Guang
Terzis, Alexandros
Helmig, Rainer
and
Weigand, Bernhard
2021.
Transport of Turbulence Across Permeable Interface in a Turbulent Channel Flow: Interface-Resolved Direct Numerical Simulation.
Transport in Porous Media,
Vol. 136,
Issue. 1,
p.
165.
Jadidi, Mohammad
Param, Hanieh Khalili
Revell, Alistair
and
Mahmoudi, Yasser
2022.
Flow leakage and Kelvin–Helmholtz instability of turbulent flow over porous media.
Physics of Fluids,
Vol. 34,
Issue. 10,
Okazaki, Yuki
Takase, Yumeto
Kuwata, Yusuke
and
Suga, Kazuhiko
2022.
Turbulent channel flows over porous rib-roughed walls.
Experiments in Fluids,
Vol. 63,
Issue. 4,
Wang, Wenkang
Lozano-Durán, Adrián
Helmig, Rainer
and
Chu, Xu
2022.
Spatial and spectral characteristics of information flux between turbulent boundary layers and porous media.
Journal of Fluid Mechanics,
Vol. 949,
Issue. ,
Jadidi, Mohammad
Param, Hanieh Khalili
and
Mahmoudi, Yasser
2023.
On the mechanism of turbulent heat transfer in composite porous-fluid systems with finite length porous blocks: Effect of porosity and Reynolds number.
International Journal of Heat and Mass Transfer,
Vol. 208,
Issue. ,
p.
124006.
Härter, J.
Martínez, D. S.
Poser, R.
Weigand, B.
and
Lamanna, G.
2023.
Coupling between a turbulent outer flow and an adjacent porous medium: High resolved Particle Image Velocimetry measurements.
Physics of Fluids,
Vol. 35,
Issue. 2,
Jadidi, Mohammad
and
Mahmoudi, Yasser
2024.
Data-driven modal analysis of turbulent momentum exchange and heat transfer in composite porous fluid systems.
Physics of Fluids,
Vol. 36,
Issue. 4,
Chu, Xu
Wang, Wenkang
and
Weigand, Bernhard
2024.
High Performance Computing in Science and Engineering '22.
p.
183.
Yang, Guang
Xu, Ran
Tian, Yusong
Guo, Songyuan
Wu, Jingyi
and
Chu, Xu
2024.
Data-driven methods for flow and transport in porous media: A review.
International Journal of Heat and Mass Transfer,
Vol. 235,
Issue. ,
p.
126149.
Seol, Chansoo
Kim, Taewoo
and
Kim, Taehoon
2024.
The effect of permeability on the flow structure of porous square cylinders.
Journal of Fluid Mechanics,
Vol. 985,
Issue. ,
Morimoto, Mahiro
Aoki, Ryoma
Kuwata, Yusuke
and
Suga, Kazuhiko
2024.
Measurements for Characteristics of Turbulence over a Streamwise Preferential Porous Substrate.
Flow, Turbulence and Combustion,
Vol. 113,
Issue. 1,
p.
71.
Chu, Xu
and
Pandey, Sandeep
2024.
Non-intrusive, transferable model for coupled turbulent channel-porous media flow based upon neural networks.
Physics of Fluids,
Vol. 36,
Issue. 2,
Xu, Pengcheng
Wang, Lingling
Xu, Jin
Wang, Zhe
Ahmerkamp, Soeren
Bartzke, Gerhard
Wu, Mengtian
Han, Jianjun
and
Zhu, Hai
2024.
Effects of porous structures on point source dispersion across the sediment–water interface.
AQUA — Water Infrastructure, Ecosystems and Society,
Vol. 73,
Issue. 1,
p.
114.
Habibi Khorasani, Seyed Morteza
Luhar, Mitul
and
Bagheri, Shervin
2024.
Turbulent flows over porous lattices: alteration of near-wall turbulence and pore-flow amplitude modulation.
Journal of Fluid Mechanics,
Vol. 984,
Issue. ,
Aghaei-Jouybari, Mostafa
Seo, Jung-Hee
Pinto, Sasindu
Cattafesta, Louis
Meneveau, Charles
and
Mittal, Rajat
2024.
Extended Darcy–Forchheimer law including inertial flow deflection effects.
Journal of Fluid Mechanics,
Vol. 980,
Issue. ,
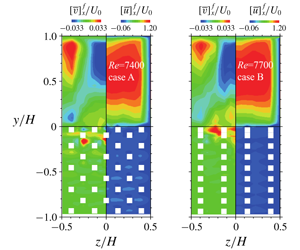
 $Re\simeq 3500$ and 7500. Cross-sectional secondary flows are detected with an enhanced magnitude of approximately 6 % of the inlet bulk velocity. The secondary flow pattern consisting of four large vortices is observed to be insensitive to the porous structures. Over the porous wall, although turbulence is enhanced by the permeability, it is confirmed that turbulence over and under the porous surfaces is rather insensitive to the wall-normal permeability compared with the streamwise permeability as seen in porous-wall channel flows. In the present range of streamwise permeability Reynolds numbers of
$Re\simeq 3500$ and 7500. Cross-sectional secondary flows are detected with an enhanced magnitude of approximately 6 % of the inlet bulk velocity. The secondary flow pattern consisting of four large vortices is observed to be insensitive to the porous structures. Over the porous wall, although turbulence is enhanced by the permeability, it is confirmed that turbulence over and under the porous surfaces is rather insensitive to the wall-normal permeability compared with the streamwise permeability as seen in porous-wall channel flows. In the present range of streamwise permeability Reynolds numbers of  $Re_{K_{x}}=2.49{-}6.37$, the wall-normal fluctuations become dominant once underneath the porous surface while the streamwise ones become dominant again deep inside the porous layer. Applying streamwise–spanwise plane averaging, which covers a 52 % area in the middle of the duct, to the flow quantities, it is confirmed that the correlations between the pore-scale Reynolds number and the log-law parameters are similar to those seen in a wide range of porous-wall channels. The above characteristics are generally the same as those of porous-wall channels in the same range of porosities and permeability Reynolds numbers even with the enhanced secondary flows. However, from the spectral analysis of flows at the porous walls, it is found that, near the symmetry planes, the wavelengths of the Kelvin–Helmholtz waves become a little shorter than those in turbulent porous-wall channels possibly because of the sidewall boundary layers, particularly at low Reynolds numbers.
$Re_{K_{x}}=2.49{-}6.37$, the wall-normal fluctuations become dominant once underneath the porous surface while the streamwise ones become dominant again deep inside the porous layer. Applying streamwise–spanwise plane averaging, which covers a 52 % area in the middle of the duct, to the flow quantities, it is confirmed that the correlations between the pore-scale Reynolds number and the log-law parameters are similar to those seen in a wide range of porous-wall channels. The above characteristics are generally the same as those of porous-wall channels in the same range of porosities and permeability Reynolds numbers even with the enhanced secondary flows. However, from the spectral analysis of flows at the porous walls, it is found that, near the symmetry planes, the wavelengths of the Kelvin–Helmholtz waves become a little shorter than those in turbulent porous-wall channels possibly because of the sidewall boundary layers, particularly at low Reynolds numbers.