No CrossRef data available.
Article contents
Characteristic length scales of strongly rotating Boussinesq flow in variable-aspect-ratio domains
Published online by Cambridge University Press: 04 October 2018
Abstract
We quantify the variability of the characteristic length scales of isotropically forced Boussinesq flows with stratification and frame rotation, as functions of the ratio 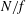 $N/f$ of the Brunt–Väisälä frequency to the Coriolis frequency. The parameter ranges
$N/f$ of the Brunt–Väisälä frequency to the Coriolis frequency. The parameter ranges 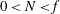 $0<N<f$, domain aspect ratio
$0<N<f$, domain aspect ratio 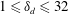 $1\leqslant \unicode[STIX]{x1D6FF}_{d}\leqslant 32$ and Burger number
$1\leqslant \unicode[STIX]{x1D6FF}_{d}\leqslant 32$ and Burger number 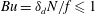 $Bu=\unicode[STIX]{x1D6FF}_{d}N/f\leqslant 1$ are explored for two values of
$Bu=\unicode[STIX]{x1D6FF}_{d}N/f\leqslant 1$ are explored for two values of 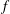 $f$, one resulting in linear potential vorticity and the other in nonlinear potential vorticity. Characteristic length scales of the wave and vortical linear eigenmodes are separately quantified using
$f$, one resulting in linear potential vorticity and the other in nonlinear potential vorticity. Characteristic length scales of the wave and vortical linear eigenmodes are separately quantified using  $n$th-order spectral moments in both horizontal and vertical directions, for integer
$n$th-order spectral moments in both horizontal and vertical directions, for integer 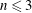 $n\leqslant 3$. In flows with linear potential vorticity, the horizontal vortical length scale
$n\leqslant 3$. In flows with linear potential vorticity, the horizontal vortical length scale 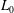 $L_{0}$, characterizing a typical width of columnar structures, grows as
$L_{0}$, characterizing a typical width of columnar structures, grows as 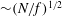 ${\sim}(N/f)^{1/2}$ at all orders of
${\sim}(N/f)^{1/2}$ at all orders of  $n$, regardless of domain aspect ratio. In unit-aspect-ratio domains, when intermediate scales are measured by filtering out the largest scales and using higher-order moments
$n$, regardless of domain aspect ratio. In unit-aspect-ratio domains, when intermediate scales are measured by filtering out the largest scales and using higher-order moments 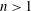 $n>1$, the vortical-mode aspect ratio
$n>1$, the vortical-mode aspect ratio 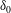 $\unicode[STIX]{x1D6FF}_{0}$ asymptotes to a scaling of
$\unicode[STIX]{x1D6FF}_{0}$ asymptotes to a scaling of 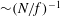 ${\sim}(N/f)^{-1}$, in agreement with quasi-geostrophic estimates. In contrast, the
${\sim}(N/f)^{-1}$, in agreement with quasi-geostrophic estimates. In contrast, the 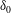 $\unicode[STIX]{x1D6FF}_{0}$ in tall-aspect-ratio domain flows yields a decay rate of at most
$\unicode[STIX]{x1D6FF}_{0}$ in tall-aspect-ratio domain flows yields a decay rate of at most  ${\sim}(N/f)^{-1/2}$ after large-scale filtering. Flows with nonlinear potential vorticity display consistently weaker dependence of the characteristic scales on
${\sim}(N/f)^{-1/2}$ after large-scale filtering. Flows with nonlinear potential vorticity display consistently weaker dependence of the characteristic scales on 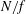 $N/f$ than the corresponding ones with linear potential vorticity. The wave-mode aspect ratios for all flows are essentially independent of
$N/f$ than the corresponding ones with linear potential vorticity. The wave-mode aspect ratios for all flows are essentially independent of 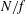 $N/f$. We highlight the differences of these flow structure scalings relative to those expected for quasi-geostrophic flows, and those observed in strongly stratified, non-quasi-geostrophic flows.
$N/f$. We highlight the differences of these flow structure scalings relative to those expected for quasi-geostrophic flows, and those observed in strongly stratified, non-quasi-geostrophic flows.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press



