Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-19T06:43:22.017Z Has data issue: false hasContentIssue false
  • English
  • Français

Cellular vortex shedding from a cylinder at low Reynolds number

Published online by Cambridge University Press:  18 March 2021

Sanjay Mittal Open the ORCID record for Sanjay Mittal [Opens in a new window] ,
Jawahar Sivabharathy Samuthira Pandi  and
Mainak Hore
Sanjay Mittal*
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Uttar Pradesh208016, India
Jawahar Sivabharathy Samuthira Pandi
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Uttar Pradesh208016, India
Mainak Hore
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Uttar Pradesh208016, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

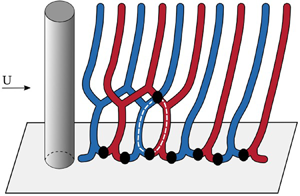
Flow past a cylinder in the presence of side walls is investigated numerically for various combinations of Reynolds numbers ($50 \leqslant \textit {Re} \leqslant 100$) and aspect ratio ($5 \leqslant AR \leqslant 90$). Various attributes such as cellular shedding, dislocations, oblique angle of vortices and their structure near the end wall are studied. The complexity of the transitions in the wake, with $\textit {Re}$, increases with increase in $AR$. The flow is associated with a single cell wake for $AR=20$, at all the $\textit {Re}$ considered. For $AR$$=90$ the flow transitions from a one-cell to two-cell wake at $\textit {Re} \sim 50$, to a four-cell structure at $\textit {Re} \sim 55$ to a three-cell wake at $\textit {Re} \sim 58$, and then to a two-cell wake at $\textit {Re} \sim 61$. The vortices near the end wall diffuse for $Re\leqslant 58$ whereas linkages form between adjacent vortices of opposite polarity at larger $Re$. The frequency of dislocations increases with increase in $\textit {Re}$. Two types of dislocations have been identified: the fork type at relatively low Re and connected fork type at larger Re. Linkages between vortices in connected fork-type dislocations may lead to ring-like structures. The end conditions and nonlinear mechanisms play a significant role in the evolution of cellular shedding. A single cell across the span is the dominant mode of shedding in the linear regime. Compared with the linear analysis, nonlinearities result in smaller oblique angles, higher shedding frequency and larger streamwise speed of the convection of vortices.

JFM classification

Wakes/Jets: Vortex streets Wakes/Jets: Wakes Vortex Flows: Vortex shedding
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A74
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Albarède, P. & Monkewitz, P.A. 1992 A model for the formation of oblique shedding and ‘chevron’ patterns in cylinder wakes. Phys. Fluids A 4 (4), 744–756.CrossRefGoogle Scholar
Albarède, P. & Provansal, M. 1995 Quasi-periodic cylinder wakes and the Ginzburg–Landau model. J. Fluid Mech. 291, 191–222.CrossRefGoogle Scholar
Barkley, D. & Henderson, R.D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Behara, S. & Mittal, S. 2009 Parallel finite element computation of incompressible flows. Parallel Comput. 35, 195–212.CrossRefGoogle Scholar
Behara, S. & Mittal, S. 2010 a Wake transition in flow past a circular cylinder. Phys. Fluids 22 (11), 114104.CrossRefGoogle Scholar
Behara, S. & Mittal, S. 2010 b Flow past a circular cylinder at low Reynolds number: Oblique vortex shedding. Phys. Fluids 22 (5), 054102.CrossRefGoogle Scholar
Berger, E. & Wille, R. 1972 Periodic flow phenomena. Ann. Rev. Fluid Mech. 4 (1), 313–340.CrossRefGoogle Scholar
Chopra, G. & Mittal, S. 2019 Drag coefficient and formation length at the onset of vortex shedding. Phys. Fluids 31 (1), 013601.CrossRefGoogle Scholar
Ding, Y. & Kawahara, M. 1998 Linear stability of incompressible flow using a mixed finite element method. J. Comput. Phys. 139 (2), 243–273.CrossRefGoogle Scholar
Eisenlohr, H. & Eckelmann, H. 1989 Vortex splitting and its consequences in the vortex street wake of cylinders at low Reynolds number. Phys. Fluids A 1 (2), 189–192.CrossRefGoogle Scholar
Gaster, M. 1971 Vortex shedding from circular cylinders at low Reynolds numbers. J. Fluid Mech. 46 (4), 749–756.CrossRefGoogle Scholar
Gerich, D. & Eckelmann, H. 1982 Influence of end plates and free ends on the shedding frequency of circular cylinders. J. Fluid Mech. 122, 109–121.CrossRefGoogle Scholar
Gerrard, J.H. 1978 The wakes of cylindrical bluff bodies at low Reynolds number. Phil. Trans. R. Soc. Lond. A 288 (1354), 351–382.Google Scholar
Hammache, M. & Gharib, M. 1989 A novel method to promote parallel vortex shedding in the wake of circular cylinders. Phys. Fluids A 1 (10), 1611–1614.CrossRefGoogle Scholar
Hammache, M. & Gharib, M. 1991 An experimental study of the parallel and oblique vortex shedding from circular cylinders. J. Fluid Mech. 232, 567–590.CrossRefGoogle Scholar
Hunt, J.C.R., Wray, A.A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Proceedings of the Summer Program, pp. 193–208. Center for Turbulence Research.Google Scholar
Jackson, C.P. 1987 A finite-element study of the onset of vortex shedding in flow past variously shaped bodies. J. Fluid Mech. 182, 23–45.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Karniadakis, G.E. & Triantafyllou, G.S. 1992 Three-dimensional dynamics and transition to turbulence in the wake of bluff objects. J. Fluid Mech. 238, 1–30.CrossRefGoogle Scholar
König, M., Eisenlohr, H. & Eckelmann, H. 1990 The fine structure in the Strouhal–Reynolds number relationship of the laminar wake of a circular cylinder. Phys. Fluids A 2 (9), 1607–1614.CrossRefGoogle Scholar
König, M., Eisenlohr, H. & Eckelmann, H. 1992 Visualization of the spanwise cellular structure of the laminar wake of wall-bounded circular cylinders. Phys. Fluids A 4 (5), 869–872.CrossRefGoogle Scholar
Kumar, B., Kottaram, J.J., Singh, A.K. & Mittal, S. 2009 Global stability of flow past a cylinder with centreline symmetry. J. Fluid Mech. 632, 273–300.CrossRefGoogle Scholar
Kumar, B. & Mittal, S. 2006 Prediction of the critical Reynolds number for flow past a circular cylinder. Comput. Meth. Appl. Mech. Engng 195 (44), 6046–6058.CrossRefGoogle Scholar
Leweke, T. & Provansal, M. 1995 The flow behind rings: bluff body wakes without end effects. J. Fluid Mech. 288, 265–310.CrossRefGoogle Scholar
Leweke, T., Provansal, M. & Boyer, L. 1993 Stability of vortex shedding modes in the wake of a ring at low Reynolds numbers. Phys. Rev. Lett. 71, 3469–3472.CrossRefGoogle ScholarPubMed
Leweke, T., Provansal, M., Miller, G.D. & Williamson, C.H.K. 1997 Cell formation in cylinder wakes at low Reynolds numbers. Phys. Rev. Lett. 78, 1259–1262.CrossRefGoogle Scholar
Liu, C.Q., Wang, Y.Q., Yang, Y. & Duan, Z. 2016 New omega vortex identification method. Sci. China Phys. Mech. 59 (8), 684711.CrossRefGoogle Scholar
Meyer, A. 1987 Modern Algorithms for Large Sparse Eigenvalue Problems. Mathematical Research, vol. 34. Akademie-Verlag.Google Scholar
Mittal, S. 2000 On the performance of high aspect ratio elements for incompressible flows. Comput. Meth. Appl. Mech. Engng 188, 269–287.CrossRefGoogle Scholar
Mittal, S. 2001 Computation of three-dimensional flows past circular cylinder of low aspect ratio. Phys. Fluids 13, 177–191.CrossRefGoogle Scholar
Mittal, S. & Dwivedi, A. 2017 Local and biglobal linear stability analysis of parallel shear flows. CMES-Comput. Model Engng 113 (2), 219–237.Google Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.CrossRefGoogle Scholar
Mittal, S., Sidharth, G.S. & Verma, A. 2014 A finite element formulation for global linear stability analysis of a nominally two-dimensional base flow. Intl J. Numer. Meth. Fluid 75, 295–312.CrossRefGoogle Scholar
Prasanth, T.K. & Mittal, S. 2008 Vortex-induced vibrations of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 594, 463–491.CrossRefGoogle Scholar
Ramberg, S.E. 1983 The effects of yaw and finite length upon the vortex wakes of stationary and vibrating circular cylinders. J. Fluid Mech. 128, 81–107.CrossRefGoogle Scholar
Saad, Y. & Schultz, M. 1986 GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7, 856–869.CrossRefGoogle Scholar
Sen, S., Mittal, S. & Biswas, G. 2009 Steady separated flow past a circular cylinder at low Reynolds numbers. J. Fluid Mech. 620, 89–119.CrossRefGoogle Scholar
Sheard, G.J., Thompson, M.C. & Hourigan, K. 2003 From spheres to circular cylinders: the stability and flow structures of bluff ring wakes. J. Fluid Mech. 492, 147–180.CrossRefGoogle Scholar
Slaouti, A. & Gerrard, J.H. 1981 An experimental investigation of the end effects on the wake of a circular cylinder towed through water at low Reynolds numbers. J. Fluid Mech. 112, 297–314.CrossRefGoogle Scholar
Stewart, G.W. 1975 Methods of simultaneous iteration for calculating eigenvectors of matrices. In Topics in Numerical Analysis II: Proceedings of the Royal Irish Academy Conference on Numerical Analysis, 1974 (ed. J.H.H. Miller), pp. 169–185. Published for the Royal Irish Academy by Academic Press.CrossRefGoogle Scholar
Stewart, G.W. 1976 Simultaneous iteration for computing invariant subspaces of non-Hermitian matrices. Numer. Math. 25 (2), 123–136.CrossRefGoogle Scholar
Tezduyar, T.C., Mittal, S., Ray, S.E. & Shih, R. 1992 Incompressible flow computations with a stabilized bilinear and linear equal-order-interpolation velocity-pressure elements. Comput. Meth. Appl. Mech. Engng 95, 203–208.CrossRefGoogle Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43 (1), 319–352.CrossRefGoogle Scholar
Tian, C., Jiang, F., Pettersen, B. & Andersson, H.I. 2017 Antisymmetric vortex interactions in the wake behind a step cylinder. Phys. Fluids 29 (10), 101704.CrossRefGoogle Scholar
Tritton, D.J. 1959 Experiments on the flow past a circular cylinder at low Reynolds numbers. J. Fluid Mech. 6 (4), 547–567.CrossRefGoogle Scholar
Wilkinson, J.H. 1965 The Algebraic Eigenvalue Problem, vol. 662. Oxford Clarendon.Google Scholar
Williamson, C.H.K. 1988 Defining a universal and continuous Strouhal–Reynolds number relationship for the laminar vortex shedding of a circular cylinder. Phys. Fluids 31 (10), 2742–2744.CrossRefGoogle Scholar
Williamson, C.H.K. 1989 Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 206, 579–627.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.CrossRefGoogle Scholar
Zhang, Y., Liu, K., Xian, H. & Du, X. 2018 A review of methods for vortex identification in hydroturbines. Renew. Sust. Energ. Rev. 81, 1269–1285.CrossRefGoogle Scholar