Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-22T14:11:44.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Cavitation about a jet in crossflow

Published online by Cambridge University Press:  04 March 2015

P. A. Brandner ,
B. W. Pearce  and
K. L. de Graaf Open the ORCID record for K. L. de Graaf [Opens in a new window]
P. A. Brandner
Affiliation:
Australian Maritime College, University of Tasmania, Launceston, TAS 7250, Australia
B. W. Pearce
Affiliation:
Australian Maritime College, University of Tasmania, Launceston, TAS 7250, Australia
K. L. de Graaf*
Affiliation:
Australian Maritime College, University of Tasmania, Launceston, TAS 7250, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Cavitation occurrence about a jet in crossflow is investigated experimentally in a variable-pressure water tunnel using still and high-speed photography. The 0.012 m diameter jet is injected on the centreplane of a 0.6 m square test section at jet to freestream velocity ratios ranging from 0.2 to 1.6, corresponding to jet-velocity-based Reynolds numbers of 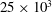$25\times 10^{3}$ to $160\times 10^{3}$ respectively. Measurements were made at a fixed freestream-based Reynolds number, for which the ratio of the undisturbed boundary layer thickness to jet diameter is 1.18. The cavitation number was varied from inception (up to about 10) down to 0.1. Inception is investigated acoustically for bounding cases of high and low susceptibility to phase change. The influence of velocity ratio and cavitation number on cavity topology and geometry are quantified from the photography. High-speed photographic recordings made at 6 kHz provide insight into cavity dynamics, and derived time series of spatially averaged pixel intensities enable frequency analysis of coherent phenomena. Cavitation inception was found to occur in the high-shear regions either side of the exiting jet and to be of an intermittent nature, increasing in occurrence and duration from 0 to 100 % probability with decreasing cavitation number or increasing jet to freestream velocity ratio. The frequency and duration of individual events strongly depends on the cavitation nuclei supply within the approaching boundary layer. Macroscopic cavitation develops downstream of the jet with reduction of the cavitation number beyond inception, the length of which has a power-law dependence on the cavitation number and a linear dependence on the jet to freestream velocity ratio. The cavity closure develops a re-entrant jet with increase in length forming a standing wave within the cavity. For sufficiently low cavitation numbers the projection of the re-entrant jet fluid no longer reaches the cavity leading edge, analogous to supercavitation forming about solid cavitators. Hairpin-shaped vortices are coherently shed from the cavity closure via mechanisms of shear-layer roll-up similar to those shed from protuberances and jets in crossflow in single-phase flows. These vortices are shed at an apparently constant frequency, independent of the jet to freestream velocity ratio but decreasing in frequency with reducing cavitation number and cavity volume growth. Highly coherent cavitating vortices form along the leading part of the cavity due to instability of the jet upstream shear layer for jet to freestream velocity ratios greater than about 0.8. These vortices are cancelled and condense as they approach the trailing edge in the shear layer of opposing vorticity associated with the cavity closure and the hairpin vortex formation. For lower velocity ratios, where there is decreased jet penetration, the jet upstream shear velocity gradient reverses and vortices of the opposite sense form, randomly modulated by boundary layer turbulence.

JFM classification

Drops and Bubbles: Cavitation Vortex Flows: Vortex shedding Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 768 , 10 April 2015 , pp. 141 - 174
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdilghanie, A., Frouzakis, C. E. & Fischer, P.2013 Direct numerical simulation of autoignition of a hydrogen jet in a preheated cross flow. In 8th US National Combustion Meeting, Paper 070LT-0251.Google Scholar
Acarlar, M. S. & Smith, C. R. 1987a A study of hairpin vortices in a laminar boundary layer. Part 1. Hairpin vortices generated by a hemisphere protuberance. J. Fluid Mech. 175, 1–41.CrossRefGoogle Scholar
Acarlar, M. S. & Smith, C. R. 1987b A study of hairpin vortices in a laminar boundary layer. Part 2. Hairpin vortices generated by fluid injection. J. Fluid Mech. 175, 43–83.Google Scholar
Acosta, A. J. & Parkin, B. R. 1975 Cavitation inception: a selective review. J. Ship Res. 19 (4), 193–205.Google Scholar
Albugues, L.2005 Analyse expérimentale et numérique d’un jet débouchant dans un écoulement tranverse. PhD thesis, École Nationale Supérieure de l’Aéronautique et de l’Espace, Université de Toulouse, France.Google Scholar
Brandner, P. A., Belle, A., Pearce, B. W. & Holmes, M. J.2012 Artificial thickening of cavitation tunnel boundary layers. In 18th Australasian Fluid Mechanics Conference, Launceston, Australia.Google Scholar
Brandner, P. A., Lecoffre, Y. & Walker, G. J.2006 Development of an Australian national facility for cavitation research. In Sixth International Symposium on Cavitation, Wageningen, The Netherlands.Google Scholar
Brandner, P. A., Lecoffre, Y. & Walker, G. J.2007 Design considerations in the development of a modern cavitation tunnel. In 16th Australasian Fluid Mechanics Conference, Gold Coast, Australia, pp. 630–637.Google Scholar
Brandner, P. A., Walker, G. J., Niekamp, P. N. & Anderson, B. 2010a An experimental investigation of cloud cavitation about a sphere. J. Fluid Mech. 656, 147–176.Google Scholar
Brandner, P. A., Wright, G., Pearce, B., Goldsworthy, L. & Walker, G. J.2010b An experimental investigation of microbubble generation in a confined turbulent jet. In 17th Australasian Fluid Mechanics Conference, Auckland, New Zealand.Google Scholar
Clarke, D. B., Brandner, P. A. & Walker, G. J. 2008 Experimental and computational investigation of flow around a 3-1 prolate spheroid. WSEAS Trans. Fluid Mech. 3 (3), 207–217.Google Scholar
Doolan, C., Brandner, P. A., Butler, D., Pearce, B., Moreau, D. & Brooks, L.2013 Hydroacoustic characterisation of the AMC cavitation tunnel. In Proceedings of Acoustics 2013, Victor Harbour, Australia.Google Scholar
Duda, B.2012 Étude et analyse numérique d’un jet chaud débouchant dans un écoulement transverse en utilisant des simulations aux échelles résolues. PhD thesis, l’Institut Supérieur de l’Aéronautique et de l’Espace, Université de Toulouse, France.Google Scholar
Fawcett, R. J., Wheeler, A. P. S., He, L. & Taylor, R. 2013 Experimental investigation into the impact of crossflow on the coherent unsteadiness within film cooling flows. Intl J. Heat Fluid Flow 40, 32–42.Google Scholar
Franc, J.-P. & Michel, J.-M. 2004 Fundamentals of Cavitation. Kluwer Academic.Google Scholar
Frechou, D., Dugue, C., Briancon-Marjollet, L., Fournier, P., Darquier, M., Descotte, L. & Merle, L.2001 Marine propulsor noise investigations in the hydroacoustic water tunnel ‘G.T.H.’. In 23rd Symposium of Naval Hydrodynamics, Val de Reuil, France.Google Scholar
Furukawa, A. & Tanaka, H. 2006 Violation of the incompressibility of liquid by simple shear flow. Nature 443, 434–438.Google Scholar
Fuster, D., Pham, K. & Zaleski, S. 2014 Stability of bubbly liquids and its connection to the process of cavitation inception. Phys. Fluids 26, 042002; 1–12.CrossRefGoogle Scholar
Gindroz, B. & Billet, M. L. 1998 Influence of the nuclei on the cavitation inception for different types of cavitation on ship propellers. Trans. ASME J. Fluids Engng 120 (1), 171–178.CrossRefGoogle Scholar
Gopalan, S., Katz, J. & Knio, O. 1999 The flow structure in the near field of jets and its effect on cavitation inception. J. Fluid Mech. 398, 1–43.Google Scholar
Guo, J., Julien, P. Y. & Meroney, R. N. 2005 Modified log-wake law for zero-pressure gradient turbulent boundary layers. J. Hydraul. Res. 43 (4), 421–430.Google Scholar
Harrington, M. K., McWaters, M. A., Bogard, D. G., Lemmon, C. A. & Thole, K. A. 2001 Full-coverage film cooling with short normal injection holes. Trans. ASME J. Turbomach. 123, 798–805.Google Scholar
Ilak, M., Schlatter, P., Bagheri, S. & Henningson, D. S. 2012 Bifurcation and stability analysis of a jet in cross-flow: onset of global instability at a low velocity ratio. J. Fluid Mech. 696, 94–121.Google Scholar
Jones, M. B., Marusic, I. & Perry, A. E. 2001 Evolution and structure of sink-flow turbulent boundary layers. J. Fluid Mech. 428, 1–27.Google Scholar
Joseph, D. D. 1998 Cavitation and the state of stress in a flowing liquid. J. Fluid Mech. 366, 367–378.Google Scholar
Jovanovic, M.2006 Film cooling through imperfect holes. PhD thesis, Technische Universiteit, Eindhoven.Google Scholar
Mahesh, K. 2013 The interaction of jets with crossflow. Annu. Rev. Fluid Mech. 45, 379–407.Google Scholar
Megerian, S., Davitian, J., Alves, L. S. de B. & Karagozian, A. 2007 Transverse-jet shear-layer instabilities. Part 1. Experimental studies. J. Fluid Mech. 593, 93–129.Google Scholar
New, T. H., Lim, T. T. & Luo, S. C. 2006 Effects of jet velocity profiles on a round jet in cross-flow. Exp. Fluids 40, 859–875.Google Scholar
Ooi, K. K. 1985 Scale effects on cavitation inception in submerged water jets: a new look. J. Fluid Mech. 151, 367–390.Google Scholar
Pauchet, J., Retailleau, A. & Woillez, J.1992 The prediction of cavitation inception in turbulent water jets. In Proceedings of the ASME Cavitation and Multiphase Flow Forum, FED, Vol. 135, Los Angeles, CA, pp. 149–158.Google Scholar
Pearce, B. & Brandner, P. 2014 Inviscid cavity flow over a wall-mounted fence. Ocean Engng 80, 13–24.CrossRefGoogle Scholar
Reisman, G. E., Duttweiler, M. E. & Brennen, C. E.1997 Effect of air injection on the cloud cavitation of a hydrofoil. In Proceedings of the ASME Fluids Engineering Division Summer Meeting, Vancouver, British Colombia, Canada, p. 3249 (10 pages).Google Scholar
Rood, E. P. 1991 Review: mechanisms of cavitation inception. Trans. ASME J. Fluids Engng 113 (2), 163–175.Google Scholar
Sallam, K. A., Aalburn, C. & Faeth, G. M. 2004 Breakup of round nonturbulent liquid jets in gaseous crossflow. AIAA J. 42, 2529–2540.Google Scholar
Sander, R.1999 Compilation of Henry’s law constants for inorganic and organic species of potential importance in environmental chemistry. http://www.henrys-law.org/henry.pdf.Google Scholar
Straka, W. A., Meyer, R. S., Fontaine, A. A. & Welz, J. P. 2010 Cavitation inception in quiescent and co-flow nozzle jets. J. Hydrodyn. 22 (5), 813–819.Google Scholar
Torrence, C. & Compo, G. P. 1998 A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79 (1), 61–78.Google Scholar

Brandner et al. supplementary movie

High-speed movie of cavitation about jet with R = 1.2 and σ = 0.2 acquired at 6 kHz, played at 30 frames per second. Shear layer vortices are evident rolling in a clockwise direction (negative vorticity) before being canceled and reversed in the positive vorticity associated with the re-entrant jet type cavity closure and hairpin formation.

Download Brandner et al. supplementary movie(Video)
Video 9 MB

Brandner et al. supplementary movie

High-speed movie of cavitation about jet with R = 1.2 and σ = 0.2 acquired at 6 kHz, played at 30 frames per second. Shear layer vortices are evident rolling in a clockwise direction (negative vorticity) before being canceled and reversed in the positive vorticity associated with the re-entrant jet type cavity closure and hairpin formation.

Download Brandner et al. supplementary movie(Video)
Video 11 MB

Brandner et al. supplementary movie

High-speed movie of cavitation about jet with R = 0.8 and σ = 0.1 acquired at 6 kHz, played at 30 frames per second. The cavity is glassy and transparent toward the leading edge as opposed to the downstream region where the cavity surface remains opaque due to the breaking wave formed by the re-entrant jet inside the cavity.

Download Brandner et al. supplementary movie(Video)
Video 7.7 MB

Brandner et al. supplementary movie

High-speed movie of cavitation about jet with R = 0.8 and σ = 0.1 acquired at 6 kHz, played at 30 frames per second. The cavity is glassy and transparent toward the leading edge as opposed to the downstream region where the cavity surface remains opaque due to the breaking wave formed by the re-entrant jet inside the cavity.

Download Brandner et al. supplementary movie(Video)
Video 8.9 MB

Brandner et al. supplementary movie

High-speed movie of cavitation about jet with R = 0.6 and σ = 0.2 acquired at 6 kHz, played at 30 frames per second. Wave-like undulations can be seen on the cavity, typical for all R < 0.8, and have the oppositive sign (ie. positive vorticity) to the shear layer vortices evident for R > 0.8.

Download Brandner et al. supplementary movie(Video)
Video 12.5 MB

Brandner et al. supplementary movie

High-speed movie of cavitation about jet with R = 0.6 and σ = 0.2 acquired at 6 kHz, played at 30 frames per second. Wave-like undulations can be seen on the cavity, typical for all R < 0.8, and have the oppositive sign (ie. positive vorticity) to the shear layer vortices evident for R > 0.8.

Download Brandner et al. supplementary movie(Video)
Video 17.6 MB

Brandner et al. supplementary movie

High-speed movie of cavitation about jet with R = 0.6 and σ = 0.6 acquired at 6 kHz, played at 30 frames per second. The high cavitation number and low velocity ratio prevent development of visible shear layer vortices.

Download Brandner et al. supplementary movie(Video)
Video 6.8 MB

Brandner et al. supplementary movie

High-speed movie of cavitation about jet with R = 0.6 and σ = 0.6 acquired at 6 kHz, played at 30 frames per second. The high cavitation number and low velocity ratio prevent development of visible shear layer vortices.

Download Brandner et al. supplementary movie(Video)
Video 6.1 MB

Brandner et al. supplementary movie

High-speed movie of cavitation about jet with R = 1.6 and σ = 0.2 acquired at 6 kHz, played at 30 frames per second. The large cavity volume causes pairing and/or merging of shear layer vortices.

Download Brandner et al. supplementary movie(Video)
Video 8.5 MB

Brandner et al. supplementary movie

High-speed movie of cavitation about jet with R = 1.6 and σ = 0.2 acquired at 6 kHz, played at 30 frames per second. The large cavity volume causes pairing and/or merging of shear layer vortices.

Download Brandner et al. supplementary movie(Video)
Video 9.7 MB

Brandner et al. supplementary movie

High-speed movie of cavitation about jet with R = 1.2 and σ = 0.6 acquired at 6 kHz, played at 30 frames per second. The cavity length is similar to the wavelength of the shear layer vortices, limiting their development before they are canceled by the counter-rotating cavity closure.

Download Brandner et al. supplementary movie(Video)
Video 9 MB

Brandner et al. supplementary movie

High-speed movie of cavitation about jet with R = 1.2 and σ = 0.6 acquired at 6 kHz, played at 30 frames per second. The cavity length is similar to the wavelength of the shear layer vortices, limiting their development before they are canceled by the counter-rotating cavity closure.

Download Brandner et al. supplementary movie(Video)
Video 10.2 MB