Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T07:32:21.861Z Has data issue: false hasContentIssue false
  • English
  • Français

The catalytic role of the beta effect in barotropization processes

Published online by Cambridge University Press:  29 August 2012

A. Venaille ,
G. K. Vallis  and
S. M. Griffies
A. Venaille*
Affiliation:
NOAA, GFDL, AOS Program, Princeton University, NJ 08540, USA Laboratoire de Physique, ENS-Lyon, 69007 Lyon, France
G. K. Vallis
Affiliation:
NOAA, GFDL, AOS Program, Princeton University, NJ 08540, USA
S. M. Griffies
Affiliation:
NOAA, GFDL, AOS Program, Princeton University, NJ 08540, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The vertical structure of freely evolving, continuously stratified, quasi-geostrophic flow is investigated. We predict the final state organization, and in particular its vertical structure, using statistical mechanics and these predictions are tested against numerical simulations. The key role played by conservation laws in each layer, including the fine-grained enstrophy, is discussed. In general, the conservation laws, and in particular that enstrophy is conserved layer-wise, prevent complete barotropization, i.e. the tendency to reach the gravest vertical mode. 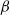The peculiar role of the effect, i.e. of the existence of planetary vorticity gradients, is discussed. In particular, it is shown that increasing 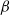increases the tendency toward barotropization through turbulent stirring. The effectiveness of barotropization may be partially parameterized using the Rhines scale 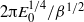. As this parameter decreases ( 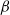increases) then barotropization can progress further, because the 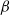term provides enstrophy to each layer. However, if the 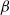effect is too large then the statistical mechanical predictions fail and wave dynamics prevent complete barotropization.

JFM classification

Geophysical and Geological Flows: Geostrophic turbulence Geophysical and Geological Flows: Quasi-geostrophic flows Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 709 , 25 October 2012 , pp. 490 - 515
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Arbic, B. K. & Flierl, G. R. 2004 Baroclinically unstable geostrophic turbulence in the limits of strong and weak bottom Ekman friction: application to midocean eddies. J. Phys. Oceanogr. 34, 2257.2.0.CO;2>CrossRefGoogle Scholar
2. Bouchet, F. 2008 Simpler variational problems for statistical equilibria of the 2D Euler equation and other systems with long range interactions. Physica D Nonlinear Phenomena 237, 1976–1981.CrossRefGoogle Scholar
3. Bouchet, F. & Corvellec, M. 2010 Invariant measures of the 2D Euler and Vlasov equations. J. Stat. Mech.: Theor. Exp. 8, 21.Google Scholar
4. Bouchet, F. & Simonnet, E. 2009 Random changes of flow topology in two-dimensional and geophysical turbulence. Phys. Rev. Lett. 102 (9), 094504.CrossRefGoogle ScholarPubMed
5. Bouchet, F. & Venaille, A. 2012 Statistical mechanics of two-dimensional and geophysical turbulent flows. Phys. Rep. 515, 227–295.CrossRefGoogle Scholar
6. Bretherton, F. P. 1966 Critical layer instability in baroclinic flows. Q. J. R. Meteorol. Soc. 92, 325–334.CrossRefGoogle Scholar
7. Bretherton, F. P. & Haidvogel, D. B. 1976 Two-dimensional turbulence above topography. J. Fluid Mech. 78, 129–154.CrossRefGoogle Scholar
8. Campa, A., Dauxois, T. & Ruffo, S. 2009 Statistical mechanics and dynamics of solvable models with long-range interactions. Phys. Rep. 480, 57–159.CrossRefGoogle Scholar
9. Carnevale, G. F. & Frederiksen, J. S. 1987 Nonlinear stability and statistical mechanics of flow over topography. J. Fluid Mech. 175, 157–181.CrossRefGoogle Scholar
10. Chaigneau, A., Le Texier, M., Eldin, G., Grados, C. & Pizarro, O. 2011 Vertical structure of mesoscale eddies in the eastern south Pacific Ocean: a composite analysis from altimetry and argo profiling floats. J. Geophys. Res. (Oceans) 116, 11025.CrossRefGoogle Scholar
11. Charney, J. G. 1971 Geostrophic turbulence. J. Atmos. Sci. 28, 1087–1094.2.0.CO;2>CrossRefGoogle Scholar
12. Chavanis, P. H. & Sommeria, J. 1996 Classification of self-organized vortices in two-dimensional turbulence: the case of a bounded domain. J. Fluid Mech. 314, 267–297.CrossRefGoogle Scholar
13. Chelton, D. B., Schlax, M. G., Samelson, R. M. & de Szoeke, R. A. 2007 Global observations of large oceanic eddies. Geophys. Res. Lett. 34, 15606.CrossRefGoogle Scholar
14. Corvellec, M. 2012 PhD thesis, chapter 3. ENS-LYON, Universite Claude Bernard.Google Scholar
15. Corvellec, M. & Bouchet, F. 2012 A complete theory of low-energy phase diagrams for two-dimensional turbulence equilibria. Preprint, arXiv:1207.1966v1.Google Scholar
16. Ellis, R. S., Haven, K. & Turkington, B. 2000 Large deviation principles and complete equivalence and nonequivalence results for pure and mixed ensembles. J. Stat. Phys. 101, 999–1064.CrossRefGoogle Scholar
17. Ferrari, R. & Wunsch, C. 2009 Ocean circulation kinetic energy: reservoirs, sources, and sinks. Annu. Rev. Fluid Mech. 41, 253–282.CrossRefGoogle Scholar
18. Frederiksen, J. S. 1991a Nonlinear stability of baroclinic flows over topography. Geophys. Astrophys. Fluid Dyn. 57, 85–97.CrossRefGoogle Scholar
19. Frederiksen, J. S. 1991b Nonlinear studies on the effects of topography on baroclinic zonal flows. Geophys. Astrophys. Fluid Dyn. 59, 57–82.CrossRefGoogle Scholar
20. Frederiksen, J. S. & Sawford, B. L. 1980 Statistical dynamics of two-dimensional inviscid flow on a sphere. J. Atmos. Sci. 37, 717–732.2.0.CO;2>CrossRefGoogle Scholar
21. Fu, L. & Flierl, G. 1980 Nonlinear energy and enstrophy transfers in a realistically stratified ocean. Dyn. Atmos. Oceans 4, 219–246.CrossRefGoogle Scholar
22. Herbert, C., Dubrulle, B., Chavanis, P.-H. & Paillard, D. 2012 Phase transitions and marginal ensemble equivalence for freely evolving flows on a rotating sphere. Phys. Rev. E 85.CrossRefGoogle ScholarPubMed
23. Johnson, G. C. & McTaggart, K. E. 2010 Equatorial Pacific 13C water eddies in the eastern subtropical South Pacific ocean. J. Phys. Oceanogr. 40, 226.CrossRefGoogle Scholar
24. Kazantsev, E., Sommeria, J. & Verron, J. 1998 Subgrid-scale eddy parameterization by statistical mechanics in a barotropic ocean model. J. Phys. Oceanogr. 28, 1017–1042.2.0.CO;2>CrossRefGoogle Scholar
25. Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417–1423.CrossRefGoogle Scholar
26. Kraichnan, R. H. & Montgomery, D. 1980 Two-dimensional turbulence. Rep. Prog. Phys. 43, 547–619.CrossRefGoogle Scholar
27. Lapeyre, G. 2009 What vertical mode does the altimeter reflect? On the decomposition in baroclinic modes and on a surface-trapped mode. J. Phys. Oceanogr. 39, 2857.CrossRefGoogle Scholar
28. Lapeyre, G. & Klein, P. 2006 Dynamics of the upper oceanic layers in terms of surface quasigeostrophy theory. J. Phys. Oceanogr. 36, 165–176.CrossRefGoogle Scholar
29. Majda, A. & Wang, X. 2006 Nonlinear Dynamics and Statistical Theories for Basic Geophysical Flows. Cambridge University Press.CrossRefGoogle Scholar
30. McWilliams, J. C., Weiss, J. B. & Yavneh, I. 1994 Anisotropy and coherent vortex structures in planetary turbulence. Science 264, 410–413.CrossRefGoogle ScholarPubMed
31. Merryfield, W. J. 1998 Effects of stratification on quasi-geostrophic inviscid equilibria. J. Fluid Mech. 354, 345–356.CrossRefGoogle Scholar
32. Michel, J. & Robert, R. 1994 Large deviations for young measures and statistical mechanics of infinite-dimensional dynamical systems with conservation law. Commun. Math. Phys. 159, 195–215.CrossRefGoogle Scholar
33. Miller, J. 1990 Statistical mechanics of Euler equations in two dimensions. Phys. Rev. Lett. 65 (17), 2137–2140.CrossRefGoogle ScholarPubMed
34. Naso, A., Chavanis, P. H. & Dubrulle, B. 2010 Statistical mechanics of two-dimensional Euler flows and minimum enstrophy states. Eur. Phys. J. B 77, 187–212.CrossRefGoogle Scholar
35. Pedlosky, J. 1982 Geophysical Fluid Dynamics. Springer.CrossRefGoogle Scholar
36. Rhines, P. B. 1975 Waves and turbulence on a -plane. J. Fluid. Mech. 69, 417–443.CrossRefGoogle Scholar
37. Rhines, P.  (Ed.) 1977 The Dynamics of Unsteady Currents. vol. 6. Wiley and Sons.Google Scholar
38. Robert, R. 1990 Etats d’equilibre statistique pour l’ecoulement bidimensionnel d’un fluide parfait. C. R. Acad. Sci. 1, 311:575–578.Google Scholar
39. Robert, R. & Sommeria, J. 1991 Statistical equilibrium states for two-dimensional flows. J. Fluid Mech. 229, 291–310.CrossRefGoogle Scholar
40. Robert, R. & Sommeria, J. 1992 Relaxation towards a statistical equilibrium state in two-dimensional perfect fluid dynamics. Phys. Rev. Lett. 69, 2776–2779.CrossRefGoogle Scholar
41. Salmon, R. 1998 Lectures on Geophysical Fluid Dynamics. Oxford University Press.CrossRefGoogle Scholar
42. Salmon, R., Holloway, G. & Hendershott, M. C. 1976 The equilibrium statistical mechanics of simple quasi-geostrophic models. J. Fluid Mech. 75, 691–703.CrossRefGoogle Scholar
43. Schecter, D. A. 2003 Maximum entropy theory and the rapid relaxation of three-dimensional quasi-geostrophic turbulence. Phys. Rev. E 68 (6), 066309.CrossRefGoogle ScholarPubMed
44. Scott, R. B. & Wang, F. 2005 Direct evidence of an oceanic inverse kinetic energy cascade from satellite altimetry. J. Phys. Oceanogr. 35, 1650.CrossRefGoogle Scholar
45. Smith, K. S. & Vallis, G. K. 2001 The scales and equilibration of midocean eddies: freely evolving flow. J. Phys. Oceanogr. 31, 554–571.2.0.CO;2>CrossRefGoogle Scholar
46. Thomas, L. N., Tandon, A. & Mahadevan, A. 2008 Sub-mesoscale processes and dynamics. In Eddy Resolving Ocean Modelling (ed. Hecht, M. W. & Hasumi, H. ), pp. 17–38 American Geophysical Union.CrossRefGoogle Scholar
47. Thompson, A. F. & Young, W. R. 2006 Scaling baroclinic eddy fluxes: vortices and energy balance. J. Phys. Oceanogr. 36, 720.CrossRefGoogle Scholar
48. Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
49. Venaille, A. 2012 Bottom trapped currents as statistical equilibrium states above topographic anomalies. J. Fluid Mech. 699.CrossRefGoogle Scholar
50. Venaille, A. & Bouchet, F. 2011a Ocanic rings and jets as statistical equilibrium states. J. Phys. Oceanogr. 41, 1860–1873.CrossRefGoogle Scholar
51. Venaille, A. & Bouchet, F. 2011b Solvable phase diagrams and ensemble inequivalence for two-dimensional and geophysical turbulent flows. J. Stat. Phys. 143, 346–380.CrossRefGoogle Scholar