Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-17T11:24:11.751Z Has data issue: false hasContentIssue false
  • English
  • Français

Capillary rise of non-aqueous liquids in cellulose sponges

Published online by Cambridge University Press:  04 April 2017

Jungchul Kim ,
Jonghyun Ha  and
Ho-Young Kim Open the ORCID record for Ho-Young Kim [Opens in a new window]
Jungchul Kim
Affiliation:
Department of Mechanical and Aerospace Engineering, Seoul National University, Seoul 08826, Korea Department of Mechanical Engineering, Texas A&M University, College Station, TX 77840, USA Department of Extreme Thermal Systems, Korea Institute of Machinery and Materials, Daejeon 34103, Korea
Jonghyun Ha
Affiliation:
Department of Mechanical and Aerospace Engineering, Seoul National University, Seoul 08826, Korea
Ho-Young Kim*
Affiliation:
Department of Mechanical and Aerospace Engineering, Seoul National University, Seoul 08826, Korea Big Data Institute, Seoul National University, Seoul 08826, Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A cellulose sponge is a mundane porous medium composed of numerous microporous cellulose sheets surrounding macroscale voids. Here, we quantify the capillary rise dynamics of non-aqueous liquids in a sponge using a combination of experiment and theory. 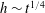Although the classical law of Washburn is obeyed in the early stages, the wet front propagation is no longer diffusive in the late stages and follows a power law, $h\sim t^{1/4}$, with 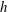$h$ and $t$ being the capillary rise height and time respectively. The transition of the power law is a consequence of the peculiar heterogeneous pore structure of cellulose sponges. The permeability and driving pressure change at the rise height above which the macro voids can no longer be filled completely due to significant effects of gravity. We rationalize the 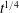$t^{1/4}$ law by considering liquid flows along the corners of macro voids driven by capillary pressure of microscale wall pores.

JFM classification

Interfacial Flows (free surface): Capillary flows Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics Low-Reynolds-number flows: Porous media
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 818 , 10 May 2017 , R2
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bell, J. M. & Cameraon, F. K. 1906 The flow of liquids through capillary spaces. J. Phys. Chem. 10, 658–674.Google Scholar
Castro-Ceseña, A. B., Camacho-Villegasb, T. A., Lugo-Fabresb, P. H., Novitskayac, E. E., McKittricka, J. & Licea-Navarrob, A. 2016 Effect of starch on the mechanical and in vitro properties of collagen-hydroxyapatite sponges for applications in dentistry. Carbohydrate Polymers 148, 78–85.Google Scholar
Chung, S., Gamcsik, M. P. & King, M. W. 2011 Novel scaffold design with multi-grooved PLA fibers. Biomed. Mater. 6, 045001.Google Scholar
Coda, R.2005 A study of cellulose based biodegradable foams and sponges. M.S. thesis, Georgia Institute of Technology.Google Scholar
Delker, T., Pengra, D. B. & Wong, P.-Z. 1996 Interface pinning and dynamics of capillary rise in porous media. Phys. Rev. Lett. 76, 2902–2905.Google Scholar
Fisher, L. 1999 Physics takes the biscuit. Nature 397, 469.CrossRefGoogle Scholar
Galan, I., Perron, L. & Glasser, F. P. 2015 Impact of chloride-rich environments on cement paste mineralogy. Cem. Concr. Res. 68, 174–183.Google Scholar
Goehring, L., Morris, S. W. & Lin, Z. 2006 An experimental investigation of the scaling of columnar joints. Phys. Rev. E 74, 036115.Google Scholar
Gorce, J.-B., Hewitt, I. J. & Vella, D. 2016 Capillary imbibition into converging tubes: beating Washburn’s law and the optimal imbibition of liquids. Langmuir 32, 1560–1567.Google Scholar
Ishino, C., Reyssat, M., Reyssat, E., Okumura, K. & Quéré, D. 2007 Wicking within forests of micropillars. Europhys. Lett. 79, 56005.CrossRefGoogle Scholar
Jurin, J. 1718 An account of some experiments shown before the Royal Society; with an enquiry into the cause of the ascent and suspension of water in capillary tubes. Phil. Trans. 30, 739–747.Google Scholar
Kim, J., Moon, M.-W. & Kim, H.-Y. 2016 Dynamics of hemiwicking. J. Fluid Mech. 800, 57–71.Google Scholar
Kim, J., Moon, M.-W., Lee, K.-R., Mahadevan, L. & Kim, H.-Y. 2011 Hydrodynamics of writing with ink. Phys. Rev. Lett. 107, 264501.CrossRefGoogle ScholarPubMed
Kim, S. J., Choi, J. W., Moon, M.-W., Lee, K.-R., Chang, Y. S., Lee, D.-Y. & Kim, H.-Y. 2015 Wicking and flooding of liquids on vertical porous sheets. Phys. Fluids. 27, 032105.Google Scholar
Kobatake, K., Mita, K. & Kato, M. 2015 Effect on hemostasis of an absorbable hemostatic gelatin sponge after transrectal prostate needle biopsy. Int. Braz. J. Urol. 41, 337–343.Google Scholar
Lago, M. & Araujo, M. 2001 Capillary rise in porous media. J. Colloid Interface Sci. 234, 35–43.Google Scholar
Lee, M., Kim, S., Kim, H.-Y. & Mahadevan, L. 2016b Bending and buckling of wet paper. Phys. Fluids 28, 042101.CrossRefGoogle Scholar
Lee, S. M., Park, I. K., Kim, Y. S., Kim, H. J., Moon, H., Mueller, S. & Jeong, Y.-I. 2016a Physical, morphological, and wound healing properties of a polyurethane foam-film dressing. Biomater. Res. 20, 15.Google Scholar
Lucas, V. R. 1918 Ueber das Zeitgesetz des kapillaren Aufstiegs von Flüssigkeiten. Kolloid Zeistschrift 23, 15–22.CrossRefGoogle Scholar
Märtson, M., Viljanto, J., Hurme, T., Laippala, P. & Saukko, P. 1999 Is cellulose sponge degradable or stable as implantation material? An in vivo subcutaneous study in rat. Biomaterials 20, 1989–1995.Google Scholar
Nia, S. F. & Jessen, K. 2015 Theoretical analysis of capillary rise in porous media. Trans. Porous Med. 110, 141–155.Google Scholar
Obara, N. & Okumura, K. 2012 Imbibition of a textured surface decorated by short pillars with rounded edges. Phys. Rev. E 86, 020601.Google Scholar
Ponomarenko, A., Quéré, D. & Clanet, C. A. 2011 A universal law for capillary rise in corners. J. Fluid Mech. 666, 146–154.Google Scholar
Reyssat, E. & Mahadevan, L. 2009 Hygromorphs: from pine cones to biomimetic bilayers. J. R. Soc. Interface 6, 951–957.CrossRefGoogle ScholarPubMed
Reyssat, M., Courbin, L., Reyssat, E. & Stone, H. A. 2008 Imbibition in geometries with axial variations. J. Fluid Mech. 615, 335–344.Google Scholar
Šelih, J., Sousa, A. C. M. & Bremner, T. A. 1994 Moisture and heat flow in concrete walls exposed to fire. J. Engng Mech.-ASCE 120, 2028–2043.Google Scholar
Siddique, J. I., Anderson, D. M. & Bondarev, A. 2009 Capillary rise of a liquid into a deformable porous material. Phys. Fluids 21, 013106.CrossRefGoogle Scholar
Take, W. A., Bolten, M. D., Wong, P. C. P. & Yeung, F. J. 2004 Evaluation of landslide triggering mechanisms in model fill slopes. Landslides 1, 173–184.Google Scholar
Vasiliev, L. L. 2008 Micro and miniature heat pipes. Appl. Therm. Engng 28, 266–273.Google Scholar
Vella, D. & Huppert, H. E. 2007 The waterlogging of floating objects. J. Fluid Mech. 585, 245–254.Google Scholar
Washburn, E. W. 1921 The dynamics of capillary flow. Phys. Rev. 17, 273–283.Google Scholar
Weislogel, M. M. 2012 Compound capillary rise. J. Fluid Mech. 709, 622–647.CrossRefGoogle Scholar
Welti-Chanes, J., Velez-Ruiz, J. F. & Barbosa-Cänovas, G. V. 2016 Transport Phenomena in Food Processing. CRC Press.Google Scholar
Yeh, T.-C. J., Guzman, A., Srivastava, R. & Gagnard, P. E. 1994 Numerical simulation of the wicking effect in linear systems. Ground Water 32, 2–11.Google Scholar
Yoon, J., Cai, S., Suo, Z. & Hayward, R. C. 2010 Poroelastic swelling kinetics of thin hydrogel layers: comparison of theory and experiment. Soft Matt. 6, 6004–6012.Google Scholar
Supplementary material: File

Kim supplementary material

Kim supplementary material 1

Download Kim supplementary material(File)
File 47.2 KB