Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T01:37:31.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Capillary levelling of immiscible bilayer films

Published online by Cambridge University Press:  25 January 2021

Vincent Bertin Open the ORCID record for Vincent Bertin [Opens in a new window] ,
Carmen L. Lee Open the ORCID record for Carmen L. Lee [Opens in a new window] ,
Thomas Salez Open the ORCID record for Thomas Salez [Opens in a new window] ,
Elie Raphaël Open the ORCID record for Elie Raphaël [Opens in a new window]  and
Kari Dalnoki-Veress Open the ORCID record for Kari Dalnoki-Veress [Opens in a new window]
Vincent Bertin
Affiliation:
Univ. Bordeaux, CNRS, LOMA, UMR 5798, 33405Talence, France UMR CNRS Gulliver 7083, ESPCI Paris, PSL Research University, 75005Paris, France
Carmen L. Lee
Affiliation:
Department of Physics and Astronomy, McMaster University, 1280 Main Street West, Hamilton, ONL8S 4M1, Canada
Thomas Salez
Affiliation:
Univ. Bordeaux, CNRS, LOMA, UMR 5798, 33405Talence, France Global Station for Soft Matter, Global Institution for Collaborative Research and Education, Hokkaido University, Sapporo, Japan
Elie Raphaël
Affiliation:
UMR CNRS Gulliver 7083, ESPCI Paris, PSL Research University, 75005Paris, France
Kari Dalnoki-Veress*
Affiliation:
Univ. Bordeaux, CNRS, LOMA, UMR 5798, 33405Talence, France Department of Physics and Astronomy, McMaster University, 1280 Main Street West, Hamilton, ONL8S 4M1, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

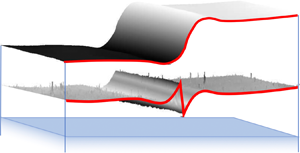
Flow in thin films is highly dependent on the boundary conditions. Here, we study the capillary levelling of thin bilayer films composed of two immiscible liquids. Specifically, a stepped polymer layer is placed atop another, flat polymer layer. The Laplace pressure gradient resulting from the curvature of the step induces flow in both layers, which dissipates the excess capillary energy stored in the stepped interface. The effect of different viscosity ratios between the bottom and top layers is investigated. We invoke a long-wave expansion of the low-Reynolds-number hydrodynamics to model the energy dissipation due to the coupled viscous flows in the two layers. Good agreement is found between the experiments and the model. Analysis of the latter further reveals an interesting double cross-over in time, from Poiseuille flow, to plug flow and finally to Couette flow. The cross-over time scales depend on the viscosity ratio between the two liquids, allowing for the dissipation mechanisms to be selected and finely tuned by varying this ratio.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 911 , 25 March 2021 , A13
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Acheson, D.J. 1990 Elementary Fluid Dynamics. Oxford University Press.Google Scholar
Backholm, M., Benzaquen, M., Salez, T., Raphaël, E. & Dalnoki-Veress, K. 2014 Capillary levelling of a cylindrical hole in a viscous film. Soft Matter 10, 2550–2558.CrossRefGoogle Scholar
Bäumchen, O., Benzaquen, M., Salez, T., McGraw, J., Backholm, M., Fowler, P., Raphaël, E. & Dalnoki-Veress, K. 2013 Relaxation and intermediate asymptotics of a rectangular trench in a viscous film. Phys. Rev. E 88, 035001.CrossRefGoogle Scholar
Bäumchen, O. & Jacobs, K. 2009 Slip effects in polymer thin films. J. Phys.: Condens. Matter 22 (3), 033102.Google ScholarPubMed
Bertin, V., Niven, J., Stone, H.A., Salez, T., Raphaël, E. & Dalnoki-Veress, K. 2020 Symmetrization of thin free-standing liquid films via capillary-driven flow. Phys. Rev. Lett. 124, 184502.CrossRefGoogle Scholar
Bironeau, A., Salez, T., Miquelard-Garnier, G. & Sollogoub, C. 2017 Existence of a critical layer thickness in PS/PMMA nanolayered films. Macromolecules 50 (10), 4064–4073.CrossRefGoogle Scholar
Bocquet, L. & Charlaix, E. 2010 Nanofluidics, from bulk to interfaces. Chem. Soc. Rev. 39, 1073–1095.CrossRefGoogle ScholarPubMed
Brochard-Wyart, F. & de Gennes, P.-G. 1990 Molécules coulissantes à une interface polymère-polymère. C.R. Acad. Sci. 317, 13–17.Google Scholar
Brochard-Wyart, F., Martin, P. & Redon, C. 1993 Liquid/liquid dewetting. Langmuir 9 (12), 3682–3690.CrossRefGoogle Scholar
Buck, E., Petersen, K., Hund, M., Krausch, G. & Johannsmann, D. 2004 Decay kinetics of nanoscale corrugation gratings on polymer surface: evidence for polymer flow below the glass temperature. Macromolecules 37 (23), 8647–8652.CrossRefGoogle Scholar
Chai, Y., Salez, T., McGraw, J., Benzaquen, M., Dalnoki-Veress, K., Raphaël, E. & Forrest, J.A. 2014 A direct quantitative measure of surface mobility in a glassy polymer. Science 343 (6174), 994–999.CrossRefGoogle Scholar
Chebil, M.S., McGraw, J.D., Salez, T., Sollogoub, C. & Miquelard-Garnier, G. 2018 Influence of outer-layer finite-size effects on the dewetting dynamics of a thin polymer film embedded in an immiscible matrix. Soft Matter 14 (30), 6256–6263.CrossRefGoogle Scholar
Erneux, T. & Davis, S.H. 1993 Nonlinear rupture of free films. Phys. Fluids A 5 (5), 1117–1122.CrossRefGoogle Scholar
Fakhraai, Z. & Forrest, J.A. 2008 Measuring the surface dynamics of glassy polymers. Science 319 (5863), 600–604.CrossRefGoogle ScholarPubMed
Fetzer, R., Jacobs, K., Münch, A., Wagner, B. & Witelski, T.P. 2005 New slip regimes and the shape of dewetting thin liquid films. Phys. Rev. Lett. 95 (12), 127801.CrossRefGoogle ScholarPubMed
de Gennes, P.-G. 1989 Adhésion de polymères légèrement incompatibles. CR Acad Sci 308, 1401–1403.Google Scholar
de Gennes, P.-G. & Brochard-Wyart, F. 1990 Glissement à l'interface de deux polymères légèrement incompatibles. C.R. Acad. Sci. 310, 1169–1173.Google Scholar
de Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2003 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.Google Scholar
Hirai, Y., Yoshikawa, T., Takagi, N., Yoshida, S. & Yamamoto, K. 2003 Mechanical properties of poly-methyl methacrylate (PMMA) for nano imprint lithography. J. Photopolym. Sci. Technol. 16 (4), 615–620.CrossRefGoogle Scholar
Hourlier-Fargette, A., Antkowiak, A., Chateauminois, A. & Neukirch, S. 2017 Role of uncrosslinked chains in droplets dynamics on silicone elastomers. Soft Matter 13, 3484–3491.CrossRefGoogle ScholarPubMed
Howell, C., et al. . 2015 Stability of surface-immobilized lubricant interfaces under flow. Chem. Mater. 27 (5), 1792–1800.CrossRefGoogle Scholar
Huang, R. & Suo, Z. 2002 Instability of a compressed elastic film on a viscous layer. Intl J. Solids Struct. 39 (7), 1791–1802.CrossRefGoogle Scholar
Ilton, M., Couchman, M., Gerbelot, C., Benzaquen, M., Fowler, P., Stone, H., Raphaël, E., Dalnoki-Veress, K. & Salez, T. 2016 Capillary leveling of freestanding liquid nanofilms. Phys. Rev. Lett. 117, 167801.CrossRefGoogle ScholarPubMed
Jachalski, S., Münch, A. & Wagner, B. 2015 Thin-film models for viscoelastic liquid bi-layers. WIAS Preprint 2187.Google Scholar
Jachalski, S., Peschka, D., Münch, A. & Wagner, B. 2014 Impact of interfacial slip on the stability of liquid two-layer polymer films. J. Engng Maths 86 (1), 9–29.Google Scholar
Kargupta, K., Sharma, A. & Khanna, R. 2004 Instability, dynamics, and morphology of thin slipping films. Langmuir 20 (1), 244–253.CrossRefGoogle ScholarPubMed
Keiser, A., Keiser, L., Clanet, C. & Quéré, D. 2017 Drop friction on liquid-infused materials. Soft Matter 13, 6981–6987.CrossRefGoogle ScholarPubMed
Koplik, J. & Banavar, J. 2006 Slip, immiscibility, and boundary conditions at the liquid-liquid interface. Phys. Rev. Lett. 96, 044505.CrossRefGoogle ScholarPubMed
Lal, J., Malkova, S., Mukhopadhyay, M.K., Narayanan, S., Fluerasu, A., Darling, S.B., Lurio, L.B. & Sutton, M. 2017 Dewetting in immiscible polymer bilayer films. Phys. Rev. Mater. 1 (1), 015601.CrossRefGoogle Scholar
Lambooy, P., Phelan, K.C., Haugg, O. & Krausch, G. 1996 Dewetting at the liquid-liquid interface. Phys. Rev. Lett. 76 (7), 1110.CrossRefGoogle ScholarPubMed
Lauga, E. & Brenner, M.P. 2004 Dynamic mechanisms for apparent slip on hydrophobic surfaces. Phys. Rev. E 70, 026311.CrossRefGoogle ScholarPubMed
Lee, P.C., Park, H.E., Morse, D.C. & Macosko, C.W. 2009 Polymer-polymer interfacial slip in multilayered films. J. Rheol. 53 (4), 893–915.CrossRefGoogle Scholar
McGraw, J., Salez, T., Bäumchen, O., Raphaël, E. & Dalnoki-Veress, K. 2012 Self-similarity and energy dissipation in stepped polymer films. Phys. Rev. Lett. 109, 128303.CrossRefGoogle ScholarPubMed
McGraw, J.D., Chan, T.S., Maurer, S., Salez, T., Benzaquen, M., Raphaël, E., Brinkmann, M. & Jacobs, K. 2016 Slip-mediated dewetting of polymer microdroplets. Proc. Natl Acad. Sci. USA 113 (5), 1168.CrossRefGoogle ScholarPubMed
McGraw, J.D., Jago, N. & Dalnoki-Veress, K. 2011 Capillary levelling as a probe of thin film polymer rheology. Soft Matter 7, 7832–7838.CrossRefGoogle Scholar
McGraw, J.D., Salez, T., Bäumchen, O., Raphaël, E. & Dalnoki-Veress, K. 2013 Capillary leveling of stepped films with inhomogeneous molecular mobility. Soft Matter 9, 8297–8305.CrossRefGoogle Scholar
Merabia, S. & Bonet Avalos, J. 2008 Dewetting of a stratified two-component liquid film on a solid substrate. Phys. Rev. Lett. 101, 208304.CrossRefGoogle ScholarPubMed
Münch, A., Wagner, B.A. & Witelski, T.P. 2005 Lubrication models with small to large slip lengths. J. Engng Maths 53 (3–4), 359–383.CrossRefGoogle Scholar
Oron, A., Davis, S. & Bankoff, S. 1997 Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69 (3), 931–980.CrossRefGoogle Scholar
Peaudecerf, F.J., Landel, J.R., Goldstein, R.E. & Luzzatto-Fegiz, P. 2017 Traces of surfactants can severely limit the drag reduction of superhydrophobic surfaces. Proc. Natl Acad. Sci. USA 114 (28), 7254–7259.CrossRefGoogle ScholarPubMed
Peschka, D., Bommer, S., Jachalski, S., Seemann, R. & Wagner, B. 2018 Impact of energy dissipation on interface shapes and on rates for dewetting from liquid substrates. Sci. Rep. 8 (1), 13295.CrossRefGoogle ScholarPubMed
Poesio, P., Damone, A. & Matar, O.K. 2017 Slip at liquid-liquid interfaces. Phys. Rev. Fluids 2 (4), 044004.CrossRefGoogle Scholar
Ponting, M., Hiltner, A. & Baer, E. 2010 Polymer nanostructures by forced assembly: process, structure, and properties. In Macromolecular Symposia, vol. 294, pp. 19–32. Wiley Online Library.CrossRefGoogle Scholar
Pototsky, A., Bestehorn, M., Merkt, D. & Thiele, U. 2004 Alternative pathways of dewetting for a thin liquid two-layer film. Phys. Rev. E 70 (2), 025201.CrossRefGoogle ScholarPubMed
Razavi, S., Koplik, J. & Kretzschmar, I. 2014 Molecular dynamics simulations: insight into molecular phenomena at interfaces. Langmuir 30 (38), 11272–11283.CrossRefGoogle ScholarPubMed
Rivetti, M., Bertin, V., Salez, T., Hui, C.-Y., Linne, C., Arutkin, M., Wu, H., Raphaël, E. & Bäumchen, O. 2017 Elastocapillary levelling of thin viscous films on soft substrates. Phys. Rev. Fluids 2, 094001.CrossRefGoogle Scholar
Rognin, E., Landis, S. & Davoust, L. 2011 Viscosity measurements of thin polymer films from reflow of spatially modulated nanoimprinted patterns. Phys. Rev. E 84, 041805.CrossRefGoogle ScholarPubMed
Salez, T., McGraw, J., Bäumchen, O., Dalnoki-Veress, K. & Raphaël, E. 2012 a Capillary-driven flow induced by a stepped perturbation atop a viscous film. Phys. Fluids 24, 102111.CrossRefGoogle Scholar
Salez, T., McGraw, J.D., Cormier, S.L., Bäumchen, O., Dalnoki-Veress, K. & Raphaël, E. 2012 b Numerical solutions of thin-film equations for polymer flows. Eur. Phys. J. E 35 (11), 114.CrossRefGoogle ScholarPubMed
Seemann, R., Herminghaus, S. & Jacobs, K. 2001 Dewetting patterns and molecular forces: a reconciliation. Phys. Rev. Lett. 86 (24), 5534–5537.CrossRefGoogle ScholarPubMed
Segalman, R.A. & Green, P.F. 1999 Dynamics of rims and the onset of spinodal dewetting at liquid/liquid interfaces. Macromolecules 32 (3), 801–807.CrossRefGoogle Scholar
Sharma, A. & Verma, R. 2004 Pattern formation and dewetting in thin films of liquids showing complete macroscale wetting: from “pancakes” to “swiss cheese”. Langmuir 20, 10337–10345.CrossRefGoogle Scholar
Stillwagon, L.E. & Larson, R.G. 1988 Fundamentals of topographic substrate leveling. J. Appl. Phys. 63 (11), 5251–5258.CrossRefGoogle Scholar
Tanaka, K., Takahara, A. & Kajiyama, T. 1996 Film thickness dependence of the surface structure of immiscible polystyrene/poly(methyl methacrylate) blends. Macromolecules 29, 3232–3239.CrossRefGoogle Scholar
Teisseire, J., Revaux, A., Foresti, M & Barthel, E. 2011 Confinement and flow dynamics in thin polymer films for nanoimprint lithography. Appl. Phys. Lett. 98, 013106.CrossRefGoogle Scholar
Wu, S. 1970 Surface and interfacial tensions of polymer melts. II. Poly(methyl methacrylate),poly(n-butyl methacrylate) and polystyrene. J. Phys. Chem. 74, 632–638.CrossRefGoogle Scholar
Xu, L., Bandyopadhyay, D, Shi, T., An, L., Sharma, A. & Joo, S.W. 2011 Dewetting kinetics of thin polymer bilayers: role of under layer. Polymer 52, 4345–4354.CrossRefGoogle Scholar
Xu, L., Zhang, H. & Shi, T. 2016 Liquid-liquid interfacial slip induced layer instability in a thin polymer bilayer. Polymer 99, 185–192.CrossRefGoogle Scholar
Yang, Z., Fujii, Y.K., Lee, Y., Lam, C.-H. & Tsui, O.K.C. 2010 Glass transition dynamics and surface layer mobility in unentangled polystyrene films. Science 328, 1676–1679.CrossRefGoogle ScholarPubMed
Zhao, R. & Macosko, C. 2002 Slip at polymer–polymer interfaces: rheological measurements on coextruded multilayers. J. Rheol. 46, 145–167.CrossRefGoogle Scholar