Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-17T11:25:18.593Z Has data issue: false hasContentIssue false
  • English
  • Français

Can a turbulent boundary layer become independent of the Reynolds number?

Published online by Cambridge University Press:  18 July 2018

L. Djenidi Open the ORCID record for L. Djenidi [Opens in a new window] ,
K. M. Talluru Open the ORCID record for K. M. Talluru [Opens in a new window]  and
R. A. Antonia
L. Djenidi*
Affiliation:
School of Mechanical Engineering, University of Newcastle, Newcastle, NSW 2308, Australia
K. M. Talluru
Affiliation:
School of Civil Engineering, The University of Sydney, Sydney, NSW 2006, Australia
R. A. Antonia
Affiliation:
School of Mechanical Engineering, University of Newcastle, Newcastle, NSW 2308, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper examines the Reynolds number (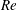$Re$) dependence of a zero-pressure-gradient (ZPG) turbulent boundary layer (TBL) which develops over a two-dimensional rough wall with a view to ascertaining whether this type of boundary layer can become independent of 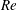$Re$. Measurements are made using hot-wire anemometry over a rough wall that consists of a periodic arrangement of cylindrical rods with a streamwise spacing of eight times the rod diameter. The present results, together with those obtained over a sand-grain roughness at high Reynolds number, indicate that a 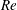$Re$-independent state can be achieved at a moderate 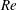$Re$. However, it is also found that the mean velocity distributions over different roughness geometries do not collapse when normalised by appropriate velocity and length scales. This lack of collapse is attributed to the difference in the drag coefficient between these geometries. We also show that the collapse of the 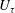$U_{\unicode[STIX]{x1D70F}}$-normalised mean velocity defect profiles may not necessarily reflect 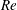$Re$-independence. A better indicator of the asymptotic state of 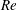$Re$ is the mean velocity defect profile normalised by the free-stream velocity and plotted as a function of 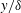$y/\unicode[STIX]{x1D6FF}$, where 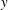$y$ is the vertical distance from the wall and 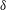$\unicode[STIX]{x1D6FF}$ is the boundary layer thickness. This is well supported by the measurements.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , pp. 1 - 22
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alfredsson, P. H. & Örlü, R. 2010 The diagnostic plot – litmus test for wall bounded turbulence data. Eur. J. Mech. (B/Fluids) 29 (6), 403–406.Google Scholar
Alfredsson, P. H., Örlü, R. & Segalini, A. 2012 A new formulation for the streamwise turbulence intensity distribution in wall-bounded turbulent flows. Eur. J. Mech. (B/Fluids) 36, 167–175.Google Scholar
Alfredsson, P. H., Segalini, A. & Örlü, R. 2011 A new scaling for the streamwise turbulence intensity in wall-bounded turbulent flows and what it tells us about the ‘outer’ peak. Phys. Fluids 23 (4), 041702.Google Scholar
Amir, M. & Castro, I. P. 2011 Turbulence in rough-wall boundary layers: universality issues. Exp. Fluids 51 (2), 313–326.Google Scholar
Antonia, R. A. & Djenidi, L. 2010 On the outer layer controversy for a turbulent boundary layer over a rough wall. In IUTAM Symposium on the Physics of Wall-bounded Turbulent Flows on Rough Walls, pp. 77–86. Springer.Google Scholar
Baars, W. J., Squire, D. T., Talluru, K. M., Abbassi, M. R., Hutchins, N. & Marusic, I. 2016 Wall-drag measurements of smooth-and rough-wall turbulent boundary layers using a floating element. Exp. Fluids 57 (5), 1–16.Google Scholar
Bakken, O. M., Krogstad, P.-Å., Ashrafian, A. & Andersson, H. I. 2005 Reynolds number effects in the outer layer of the turbulent flow in a channel with rough walls. Phys. Fluids 17 (6), 065101.Google Scholar
Bhaganagar, K., Kim, J. & Coleman, G. 2004 Effect of roughness on wall-bounded turbulence. Flow Turbul. Combust. 72 (2–4), 463–492.Google Scholar
Castro, I. P., Segalini, A. & Alfredsson, P. H. 2013 Outer-layer turbulence intensities in smooth- and rough-wall boundary layers. J. Fluid Mech. 727, 119–131.Google Scholar
Chauhan, K. A., Nagib, H. M. & Monkewitz, P. A. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41, 021404.Google Scholar
De Graaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Djenidi, L. & Antonia, R. A. 2012 A spectral chart method for estimating the mean turbulent kinetic energy dissipation rate. Exp. Fluids 53 (4), 1005–1013.Google Scholar
Djenidi, L., Antonia, R. A., Amielh, M. & Anselmet, F. 2008 A turbulent boundary layer over a two-dimensional rough wall. Exp. Fluids 44 (1), 37–47.Google Scholar
Fernholz, H. H. & Finley, P. J. 1996 The incompressible zero-pressure-gradient turbulent boundary layer: an assessment of the data. Prog. Aeronaut. Sci. 32 (4), 245–311.Google Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32 (1), 519–571.Google Scholar
Flack, K. A., Schultz, M. P. & Shapiro, T. A. 2005 Experimental support for Townsend’s Reynolds number similarity hypothesis on rough walls. Phys. Fluids 17 (3), 035102.Google Scholar
George, W. K. 1989 The self-preservation of turbulent flows and its relation to initial conditions and coherent structures. Advances in Turbulence, pp. 39–73.Google Scholar
George, W. K. & Castillo, L. 1997 Zero-pressure-gradient turbulent boundary layer. Appl. Mech. Rev. 50 (12), 689–729.Google Scholar
Hinze, J. O. 1975 Turbulence. McGraw-Hill.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18 (1), 011702.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108 (9), 094501.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Jackson, P. S. 1981 On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 111, 15–25.Google Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Jones, M. B., Nickels, T. B. & Marusic, I. 2008 On the asymptotic similarity of the zero-pressure-gradient turbulent boundary layer. J. Fluid Mech. 616, 195–203.Google Scholar
Kamruzzaman, M., Djenidi, L., Antonia, R. A. & Talluru, K. M. 2015 Drag of a turbulent boundary layer with transverse 2D circular rods on the wall. Exp. Fluids 56 (6), 1–8.Google Scholar
Klewicki, J. C. & Falco, R. E. 1990 On accurately measuring statistics associated with small-scale structure in turbulent boundary layers using hot-wire probes. J. Fluid Mech. 219, 119–142.Google Scholar
Krogstad, P.-Å. & Antonia, R. A. 1999 Surface roughness effects in turbulent boundary layers. Exp. Fluids 27 (5), 450–460.Google Scholar
Krogstad, P.-Å., Antonia, R. A. & Browne, L. W. B. 1992 Comparison between rough-and smooth-wall turbulent boundary layers. J. Fluid Mech. 245, 599–617.Google Scholar
Krogstad, P.-Å. & Efros, V. 2010 Rough wall skin friction measurements using a high resolution surface balance. Intl J. Heat Fluid Flow 31 (3), 429–433.Google Scholar
Krogstad, P.-Å. & Efros, V. 2012 About turbulence statistics in the outer part of a boundary layer developing over two-dimensional surface roughness. Phys. Fluids 24 (7), 075112.Google Scholar
Lee, J. H., Lee, S. H., Kim, K. & Sung, H. J. 2009 Structure of the turbulent boundary layer over a rod-roughened wall. Intl J. Heat Fluid Flow 30 (6), 1087–1098.Google Scholar
Lee, S. H. & Sung, H. J. 2007 Direct numerical simulation of the turbulent boundary layer over a rod-roughened wall. J. Fluid Mech. 584, 125–146.Google Scholar
Leonardi, S., Orlandi, P., Djenidi, L. & Antonia, R. A. 2015 Heat transfer in a turbulent channel flow with square bars or circular rods on one wall. J. Fluid Mech. 776, 512–530.Google Scholar
Leonardi, S., Orlandi, P., Smalley, R. J., Djenidi, L. & Antonia, R. A. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 491, 229–238.Google Scholar
Ligrani, P. M. & Bradshaw, P. 1987 Spatial resolution and measurement of turbulence in the viscous sublayer using subminiature hot-wire probes. Exp. Fluids 5 (6), 407–417.Google Scholar
Marusic, I., Chauhan, K. A., Kulandaivelu, V. & Hutchins, N. 2015 Evolution of zero-pressure-gradient boundary layers from different tripping conditions. J. Fluid Mech. 783, 379–411.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22 (6), 065103.Google Scholar
Metzger, M. M., Klewicki, J. C., Bradshaw, K. L. & Sadr, R. 2001 Scaling the near-wall axial turbulent stress in the zero pressure gradient boundary layer. Phys. Fluids 13, 1819–1821.Google Scholar
Monkewitz, P. A. & Nagib, H. M. 2015 Large-Reynolds-number asymptotics of the streamwise normal stress in zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 783, 474–503.Google Scholar
Monty, J. P., Chong, M. S., Mathis, R., Hutchins, N., Marusic, I. & Allen, J. J. 2010 A high Reynolds number turbulent boundary layer with regular ‘Braille-type’ roughness. In IUTAM Symposium on the Physics of Wall-bounded Turbulent Flows on Rough Walls, pp. 69–75. Springer.Google Scholar
Morrison, J. F., McKeon, B. J., Jiang, W. & Smits, A. J. 2004 Scaling of the streamwise velocity component in turbulent pipe flow. J. Fluid Mech. 508, 99–131.Google Scholar
Nickels, T. B. 2010 IUTAM Symposium on The Physics of Wall-Bounded Turbulent Flows on Rough Walls. Springer.Google Scholar
Örlü, R., Segalini, A., Klewicki, J. & Alfredsson, P. H. 2016 High-order generalisation of the diagnostic scaling for turbulent boundary layers. J. Turbul. 17 (7), 664–677.Google Scholar
Raupach, M. R. 1981 Conditional statistics of Reynolds stress in rough-wall and smooth-wall turbulent boundary layers. J. Fluid Mech. 108, 363–382.Google Scholar
Rotta, J. C. 1962 Turbulent boundary layers in incompressible flow. Prog. Aerosp. Sci. 2 (1), 1–95.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Squire, D. T., Morrill-Winter, C., Hutchins, N., Schultz, M. P., Klewicki, J. C. & Marusic, I. 2016 Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers. J. Fluid Mech. 795, 210–240.Google Scholar
Tachie, M. F., Bergstrom, D. J. & Balachandar, R. 2000 Rough wall turbulent boundary layers in shallow open channel flow. J. Fluids Engng 122 (3), 533–541.Google Scholar
Talluru, K. M., Djenidi, L., Kamruzzaman, M. & Antonia, R. A. 2016 Self-preservation in a zero pressure gradient rough wall turbulent boundary layer. J. Fluid Mech. 788, 57–69.Google Scholar
Talluru, K. M., Kulandaivelu, V., Hutchins, N. & Marusic, I. 2014 A calibration technique to correct sensor drift issues in hot-wire anemometry. Meas. Sci. Technol. 25 (10), 105304.Google Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vincenti, P., Klewicki, J., Morrill-Winter, C., White, C. M. & Wosnik, M. 2013 Streamwise velocity statistics in turbulent boundary layers that spatially develop to high Reynolds number. Exp. Fluids 54 (12), 1–13.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2007 Turbulence structure in rough-and smooth-wall boundary layers. J. Fluid Mech. 592, 263–293.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2011 Turbulence structure in boundary layers over periodic two-and three-dimensional roughness. J. Fluid Mech. 676, 172–190.Google Scholar
Wang, L., Hejcik, J. & Sunden, B. 2007 PIV measurement of separated flow in a square channel with streamwise periodic ribs on one wall. J. Fluids Engng 129 (7), 834–841.Google Scholar
Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.Google Scholar