1. Introduction
Bursting bubbles at a liquid–gas interface is a fundamental hydrodynamic process that has piqued interest in various fields across multiple scales ranging from food processing industry (Woodcock et al. Reference Woodcock, Kientzler, Arons and Blanchard1953; MacIntyre Reference MacIntyre1972) to oceanic wave breaking (Veron Reference Veron2015; Blanco-Rodríguez & Gordillo Reference Blanco-Rodríguez and Gordillo2020; Deike Reference Deike2022). A typical daily realization of bubble bursting occurs in a glass of champagne or other sparkling wine and is often credited for enhancing the mouthfeel of the taster (Ghabache et al. Reference Ghabache, Antkowiak, Josserand and Séon2014, Reference Ghabache, Liger-Belair, Antkowiak and Séon2016; Séon & Liger-Belair Reference Séon and Liger-Belair2017). Bubble bursting also plays a wider role in liquid fragmentation (Villermaux Reference Villermaux2020) and serves as a significant mechanism in facilitating the mass transfer of substances across the liquid–gas interface including transporting pathogens from contaminated water (Blanchard & Syzdek Reference Blanchard and Syzdek1970; Poulain & Bourouiba Reference Poulain and Bourouiba2018; Bourouiba Reference Bourouiba2021a; Ji, Singh & Feng Reference Ji, Singh and Feng2022). The interactions of such bubbles with complex rheological fluids abound in nature. For example, the elastic and plastic fluid properties govern and influence pathogen transmission, and the pathogens might even adapt to or manipulate the chemical properties of the carrier fluids to benefit their own transmission (Bourouiba Reference Bourouiba2021b). Additionally, the presence of contaminants, surfactants and oils in the marine boundary layer alters the bursting phenomenon and thereby affects the production of fine marine spray (Ji, Yang & Feng Reference Ji, Yang and Feng2021; Néel, Erinin & Deike Reference Néel, Erinin and Deike2022; Pierre, Poujol & Séon Reference Pierre, Poujol and Séon2022; Ji et al. Reference Ji, Yang, Wang, Ewoldt and Feng2023). The rheological response of food products (Ahmed & Basu Reference Ahmed and Basu2016; Mathijssen et al. Reference Mathijssen, Lisicki, Prakash and Mossige2023) exemplifies yet another instance of the importance of understanding the mechanisms of bubble bursting in rheologically complex fluids. Such an understanding will also improve our knowledge of other natural phenomena, such as volcanic eruptions and underwater gas seep (Gonnermann & Manga Reference Gonnermann and Manga2007).
Unlike the rheologically simpler Newtonian fluids, elastic and plastic properties of the complex fluid govern the bubble bursting in addition to other factors such as buoyancy, surface tension and viscosity. As an air bubble rises within the surrounding medium due to difference in density and approaches the liquid–air interface (figure 1a), the thin liquid film gradually drains (Allan, Charles & Mason Reference Allan, Charles and Mason1961) and subsequently ruptures, resulting in the formation of an open cavity (as illustrated in figure 1b) (Mason Reference Mason1954; Zhang, Cui & Wang Reference Zhang, Cui and Wang2013). The open cavity is unstable due to large surface energy. It thereby collapses, leading to a sequence of dynamic events, including the propagation of capillary waves, which can potentially result in a Worthington jet (Gekle & Gordillo Reference Gekle and Gordillo2010; Gordillo & Rodríguez-Rodríguez Reference Gordillo and Rodríguez-Rodríguez2019). The Worthington jet may destabilize due to the Rayleigh–Plateau instability, leading to the formation of small droplets (Gordillo & Gekle Reference Gordillo and Gekle2010; Ghabache et al. Reference Ghabache, Antkowiak, Josserand and Séon2014).

Figure 1. Initial condition for bubble bursting: (a) gas bubble approaches the free interface forming a film of thickness ![]() $\delta$; (b) the thin film is removed, resulting in a bubble cavity which is considered as the initial condition in our simulations.
$\delta$; (b) the thin film is removed, resulting in a bubble cavity which is considered as the initial condition in our simulations.
Early studies of bubble bursting began with a combination of experimental investigations and theoretical analyses, laying the foundation for identifying the underlying physics of the bursting mechanism in Newtonian fluids. With the progress in direct numerical simulation of multiphase flows (Popinet Reference Popinet2003, Reference Popinet2009), Deike et al. (Reference Deike, Ghabache, Liger-Belair, Das, Zaleski, Popinet and Séon2018) provided quantitative cross-validation of numerical and experimental studies. Further studies through a combination of experimental, numerical and theoretical predictions (Duchemin et al. Reference Duchemin, Popinet, Josserand and Zaleski2002; Walls, Henaux & Bird Reference Walls, Henaux and Bird2015; Berny et al. Reference Berny, Deike, Séon and Popinet2020) revealed that the formation of droplets from the jet in the bubble-bursting process is primarily determined by the viscous and gravitational effects.
On the other hand, the behaviour of bubble bursting in a different rheological medium has received less attention. Very recently, researchers have focused on studying the behaviour of such bubbles in non-Newtonian fluids (Sanjay, Lohse & Jalaal Reference Sanjay, Lohse and Jalaal2021; Ji et al. Reference Ji, Yang, Wang, Ewoldt and Feng2023; Rodríguez-Díaz et al. Reference Rodríguez-Díaz, Rubio, Montanero, Gañán-Calvo and Cabezas2023; Dixit et al. Reference Dixit, Oratis, Zinelis, Lohse and Sanjay2024), as they exhibit unique flow characteristics that can significantly affect the bursting dynamics. Notably, Rodríguez-Díaz et al. (Reference Rodríguez-Díaz, Rubio, Montanero, Gañán-Calvo and Cabezas2023) explored the phenomenon of bubble bursting in the presence of polymeric molecules, accounting for elastic effects induced by polymers. Their study revealed that the droplet emission is hindered due to extensional thickening in the jet. Another class of non-Newtonian fluids, called yield-stress fluids, exhibits a combination of solid and fluid behaviours. A thorough description and review of yield-stress fluids can be found in, for example, Balmforth, Frigaard & Ovarlez (Reference Balmforth, Frigaard and Ovarlez2014). Within the category of yield-stress fluids, a specific type known as viscoplastic fluid acts as a rigid solid below the yield stress and flows like a viscous fluid when the shear stress exceeds the material's yield stress. The capillary flows of viscoplastic fluids have been studied for various droplets (Jalaal, Stoeber & Balmforth Reference Jalaal, Stoeber and Balmforth2021; van der Kolk, Tieman & Jalaal Reference van der Kolk, Tieman and Jalaal2023) and bubble problems (Jalaal & Balmforth Reference Jalaal and Balmforth2016; Pourzahedi et al. Reference Pourzahedi, Chaparian, Roustaei and Frigaard2022; Shemilt et al. Reference Shemilt, Horsley, Jensen, Thompson and Whitfield2022, Reference Shemilt, Horsley, Jensen, Thompson and Whitfield2023). Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021) studied the bubble-bursting process in a viscoplastic fluid and revealed how viscoplasticity influences the inertiocapillary waves that drive the bubble-bursting mechanism. Unlike Newtonian liquids, the cavity can sustain shear stress (and a non-flat final shape) if the driving stresses inside the pool fall below the yield stress.
Yield-stress liquids often exhibit elastic behaviour below the yield criterion and also after yielding (Larson Reference Larson1999). This characteristic gives rise to a distinct subset within the category of yield-stress fluids, referred to as elastoviscoplastic (EVP) fluids, which behaves akin to an elastic solid below the critical stress identified by the yield stress while exhibiting a viscoelastic fluid behaviour above the yield stress. Different models have been proposed to constitute the behaviour of EVP fluids based on various steady and unsteady flow responses. In the present study, we utilize the EVP model proposed by Saramito (Reference Saramito2007). This model behaves as a Kelvin–Voigt viscoelastic solid prior to yielding and transitions to a nonlinear viscoelastic liquid in the yielded region, exhibiting Oldroyd-B viscoelastic behaviour far beyond the yield point. A detailed review of different EVP models can be found in Fraggedakis, Dimakopoulos & Tsamopoulos (Reference Fraggedakis, Dimakopoulos and Tsamopoulos2016). The physics of EVP fluids have been explored in a variety of problem sets, such as droplet deformation, deformation in shear flow (Izbassarov & Tammisola Reference Izbassarov and Tammisola2020), particle migration (Chaparian et al. Reference Chaparian, Ardekani, Brandt and Tammisola2020a), channel flow (Izbassarov et al. Reference Izbassarov, Rosti, Brandt and Tammisola2021), bubble migration (Feneuil et al. Reference Feneuil, Iqbal, Jensen, Brandt, Tammisola and Carlson2023), porous media flow (Chaparian et al. Reference Chaparian, Izbassarov, de Vita, Brandt and Tammisola2020b), rising bubble (Moschopoulos et al. Reference Moschopoulos, Spyridakis, Varchanis, Dimakopoulos and Tsamopoulos2021) and droplet spreading (França, Jalaal & Oishi Reference França, Jalaal and Oishi2024).
Given that a yield-stress fluid exhibits elastic behaviour, it becomes imperative to understand the role of elastic-stress-relaxation in driving capillary wave propagation, which, in turn, influences the formation of jets and droplets, which are the critical characteristics observed in the bubble-bursting process. This study expands the present understanding of bubble bursting (and in general interfacial flows) of EVP fluids, towards more realistic situations, which may exhibit additional phenomena such as shear thinning and complex initial bubble shape.
The paper is organized as follows. The methodology and the description of the problem are introduced in § 2. In § 3, the results obtained with different combinations of dimensionless elastic stress relaxation time and dimensionless yield stress of the EVP fluid are discussed. The §§ 3.1–3.6 delve into identifying the influence of the fluid properties on key bursting characteristics. The different modes of energy transfer are presented in § 3.7. The summary and conclusions of the present work are highlighted in § 4. Additional details about the derivation of governing equations, the log-conformation technique to solve for the extra stress in EVP, grid convergence of results, comparison between Bingham and EVP model at the viscoplastic limit, derivation of energy budget terms, energy-based analysis to understand the behaviour of maximum jet height can be, respectively, found in Appendices A–F.
2. Numerical framework
2.1. Conservation laws and constitutive equations
A small axisymmetric bubble with an initial radius of ![]() $R_0$ is placed on the surface of an incompressible EVP fluid (see § 2.3). For the considered problem, the dimensionless governing equations are
$R_0$ is placed on the surface of an incompressible EVP fluid (see § 2.3). For the considered problem, the dimensionless governing equations are
where the velocity field ![]() $\boldsymbol {u}$ and the time
$\boldsymbol {u}$ and the time ![]() $t$ are normalized using the inertiocapillary velocity (
$t$ are normalized using the inertiocapillary velocity (![]() $V_\gamma = \sqrt {\gamma /\rho _l R_0}$) and time (
$V_\gamma = \sqrt {\gamma /\rho _l R_0}$) and time (![]() $T_\gamma = \sqrt {\rho _lR_0^3/\gamma }$) scales, respectively, (here,
$T_\gamma = \sqrt {\rho _lR_0^3/\gamma }$) scales, respectively, (here, ![]() $\gamma$ and
$\gamma$ and ![]() $\rho _l$ are the surface tension and density of the liquid medium, respectively, see Appendix A for details). The pressure
$\rho _l$ are the surface tension and density of the liquid medium, respectively, see Appendix A for details). The pressure ![]() $p$, the solvent stress
$p$, the solvent stress ![]() $\boldsymbol {\tau _s}$ and the elastic stress
$\boldsymbol {\tau _s}$ and the elastic stress ![]() $\boldsymbol {\tau _p}$ are normalized using the capillary stress
$\boldsymbol {\tau _p}$ are normalized using the capillary stress ![]() $p_\gamma = \gamma /R_0$. Lastly,
$p_\gamma = \gamma /R_0$. Lastly, ![]() $\boldsymbol {f} = \boldsymbol {f}_g + \boldsymbol {f}_\gamma$ contains the contributions from gravity
$\boldsymbol {f} = \boldsymbol {f}_g + \boldsymbol {f}_\gamma$ contains the contributions from gravity ![]() $\boldsymbol {f}_g = -{\textit {Bo}}\boldsymbol {\hat {e}_z}$, where the Bond number
$\boldsymbol {f}_g = -{\textit {Bo}}\boldsymbol {\hat {e}_z}$, where the Bond number
with ![]() $g$ as acceleration due to gravity, is the ratio between hydrostatic and capillary pressures, and surface tension
$g$ as acceleration due to gravity, is the ratio between hydrostatic and capillary pressures, and surface tension ![]() $\boldsymbol {f}_\gamma = \kappa \delta _s \boldsymbol {\hat {n}}$. Here,
$\boldsymbol {f}_\gamma = \kappa \delta _s \boldsymbol {\hat {n}}$. Here, ![]() $\kappa$ is the curvature of the liquid–gas interface having a normal vector
$\kappa$ is the curvature of the liquid–gas interface having a normal vector ![]() $\boldsymbol {\hat {n}}$, and
$\boldsymbol {\hat {n}}$, and ![]() $\delta _s$ is a Dirac delta function concentrated at the interface.
$\delta _s$ is a Dirac delta function concentrated at the interface.
In (2.2), the deviatoric viscous stress tensor is
where ![]() $\boldsymbol {\mathcal {D}} = (\boldsymbol {\nabla } \boldsymbol {u} + (\boldsymbol {\nabla } \boldsymbol {u})^{\rm T})/2$ is the deformation rate tensor and
$\boldsymbol {\mathcal {D}} = (\boldsymbol {\nabla } \boldsymbol {u} + (\boldsymbol {\nabla } \boldsymbol {u})^{\rm T})/2$ is the deformation rate tensor and ![]() ${{\textit {Oh}}}_s$ denotes the solvent-Ohnesorge number which measures the inertial-capillary time scale compared with the inertial-viscous time scale as defined by
${{\textit {Oh}}}_s$ denotes the solvent-Ohnesorge number which measures the inertial-capillary time scale compared with the inertial-viscous time scale as defined by
Here, ![]() $\mu _s$ identifies the solvent-viscosity of the fluid with the total viscosity of the fluid
$\mu _s$ identifies the solvent-viscosity of the fluid with the total viscosity of the fluid ![]() $(\mu _l = \mu _s + \mu _p)$ including the contribution from polymeric-viscosity term
$(\mu _l = \mu _s + \mu _p)$ including the contribution from polymeric-viscosity term ![]() $(\mu _p)$. We can also define a polymeric-Ohnesorge number
$(\mu _p)$. We can also define a polymeric-Ohnesorge number ![]() ${{\textit {Oh}}}_p$ given by
${{\textit {Oh}}}_p$ given by
based on polymeric viscosity. Consequently, the ratio of solvent to total viscosity is
where ![]() ${{\textit {Oh}}} = {{\textit {Oh}}}_s + {{\textit {Oh}}}_p$ corresponds to the Ohnesorge number based on the total viscosity of the fluid.
${{\textit {Oh}}} = {{\textit {Oh}}}_s + {{\textit {Oh}}}_p$ corresponds to the Ohnesorge number based on the total viscosity of the fluid.
The extra stress tensor ![]() $\boldsymbol {\tau _p}$ embeds the elastic and plastic behaviour of the EVP fluid and is modelled with the constitutive relationship proposed by Saramito (Reference Saramito2007). Using an order parameter
$\boldsymbol {\tau _p}$ embeds the elastic and plastic behaviour of the EVP fluid and is modelled with the constitutive relationship proposed by Saramito (Reference Saramito2007). Using an order parameter ![]() $\boldsymbol {A}$ (conformation tensor) tracking the stretch of the EVP matrix (Snoeijer et al. Reference Snoeijer, Pandey, Herrada and Eggers2020; Stone, Shelley & Boyko Reference Stone, Shelley and Boyko2023) with a base state
$\boldsymbol {A}$ (conformation tensor) tracking the stretch of the EVP matrix (Snoeijer et al. Reference Snoeijer, Pandey, Herrada and Eggers2020; Stone, Shelley & Boyko Reference Stone, Shelley and Boyko2023) with a base state ![]() $\boldsymbol {A} = \boldsymbol {I}$ (here,
$\boldsymbol {A} = \boldsymbol {I}$ (here, ![]() $\boldsymbol {I}$ is the identity tensor), this constitutive model can be summarized as
$\boldsymbol {I}$ is the identity tensor), this constitutive model can be summarized as
and
Here, the Deborah number
is the dimensionless relaxation time ![]() $\lambda$ of the EVP matrix to its base state
$\lambda$ of the EVP matrix to its base state ![]() $\boldsymbol {A} = \boldsymbol {I}$, normalized using the inertial-capillary time scale
$\boldsymbol {A} = \boldsymbol {I}$, normalized using the inertial-capillary time scale ![]() $T_\gamma$. In (2.8),
$T_\gamma$. In (2.8), ![]() $\boldsymbol {\overset {\nabla }{A}}$ is the upper-convected time derivative and
$\boldsymbol {\overset {\nabla }{A}}$ is the upper-convected time derivative and ![]() $\|\boldsymbol {\tau _d}\|$ is the second invariant of the deviatoric part of the elastic stress tensor and are defined as
$\|\boldsymbol {\tau _d}\|$ is the second invariant of the deviatoric part of the elastic stress tensor and are defined as
and
respectively. Here, ![]() $\boldsymbol {\nabla } \boldsymbol {u} := \partial u_j/x_i$ in Einstein notation. The deviatoric part of the elastic stress tensor is calculated as
$\boldsymbol {\nabla } \boldsymbol {u} := \partial u_j/x_i$ in Einstein notation. The deviatoric part of the elastic stress tensor is calculated as ![]() $\boldsymbol {\tau _d} = \boldsymbol {\tau _p} - (\mathrm {tr} (\boldsymbol {\tau _p})/\mathrm {tr}(\boldsymbol {I}))\boldsymbol {I}$. Lastly, the plastocapillary number
$\boldsymbol {\tau _d} = \boldsymbol {\tau _p} - (\mathrm {tr} (\boldsymbol {\tau _p})/\mathrm {tr}(\boldsymbol {I}))\boldsymbol {I}$. Lastly, the plastocapillary number ![]() $(\mathcal {J})$ accounts for the competition between the yield stress
$(\mathcal {J})$ accounts for the competition between the yield stress ![]() $\tau _y$ and the Laplace pressure
$\tau _y$ and the Laplace pressure ![]() $\gamma /R_0$ as
$\gamma /R_0$ as
In (2.8), ![]() $K$ is a dimensionless function that acts as a stress-dependent switch, controlling the transition from viscoelastic solid-like to viscoelastic fluid-like behaviour in the EVP fluid. Consequently, in the yielded state
$K$ is a dimensionless function that acts as a stress-dependent switch, controlling the transition from viscoelastic solid-like to viscoelastic fluid-like behaviour in the EVP fluid. Consequently, in the yielded state ![]() ${{\textit {De}}}/K$ can be interpreted as the effective relaxation time. Consequently, below the yield stress (
${{\textit {De}}}/K$ can be interpreted as the effective relaxation time. Consequently, below the yield stress (![]() $K = 0$),
$K = 0$), ![]() $\boldsymbol {\overset {\nabla }{A}} = \boldsymbol {0}$ and the EVP matrix deform according to the flow field (see (2.11) and Stone et al. (Reference Stone, Shelley and Boyko2023)) but do not relax. Additionally, the stress
$\boldsymbol {\overset {\nabla }{A}} = \boldsymbol {0}$ and the EVP matrix deform according to the flow field (see (2.11) and Stone et al. (Reference Stone, Shelley and Boyko2023)) but do not relax. Additionally, the stress ![]() $\boldsymbol {\tau _p} = {{\textit {Oh}}}_p(\boldsymbol {A} - \boldsymbol {I})/{{\textit {De}}}$ depends only on the elastic (polymeric) deformation and the elastocapillary number
$\boldsymbol {\tau _p} = {{\textit {Oh}}}_p(\boldsymbol {A} - \boldsymbol {I})/{{\textit {De}}}$ depends only on the elastic (polymeric) deformation and the elastocapillary number
where ![]() $G = \mu _p/\lambda$ is the elastic modulus. Above the yield stress (
$G = \mu _p/\lambda$ is the elastic modulus. Above the yield stress (![]() $K > 0$), the EVP fluid behaves like a viscoelastic liquid following the constitutive relation given by combining (2.8)–(2.9) to give
$K > 0$), the EVP fluid behaves like a viscoelastic liquid following the constitutive relation given by combining (2.8)–(2.9) to give
We also model the gas-phase with the corresponding conservation laws, which are similar to (2.1) and (2.2) (see Appendix A). We keep the gas–liquid density ratio ![]() $\rho _r$
$\rho _r$ ![]() $(=\rho _g/\rho _l)$ fixed at
$(=\rho _g/\rho _l)$ fixed at ![]() $10^{-3}$. Similarly, the viscosity ratio
$10^{-3}$. Similarly, the viscosity ratio ![]() $\mu _r$
$\mu _r$ ![]() $(=\mu _g/\mu _l)$ is set constant at
$(=\mu _g/\mu _l)$ is set constant at ![]() $2\times 10^{-2}$ throughout the work.
$2\times 10^{-2}$ throughout the work.
2.2. Simulation set-up
The direct numerical simulations are performed with the open-source software language Basilisk C (Popinet Reference Popinet2009; Popinet & Collaborators Reference Popinet2024), which offers adaptive mesh refinement (AMR) based on wavelet estimated discretization errors, making it well-suited for singular interfacial flows (Berny et al. Reference Berny, Deike, Séon and Popinet2020; Sanjay Reference Sanjay2022; Yang et al. Reference Yang, Ji, Ault and Feng2023). Basilisk C uses a volume of fluid technique to track the interface with the help of a colour function ![]() $c$ (
$c$ (![]() $c = 1$ in liquid and
$c = 1$ in liquid and ![]() $c = 0$ in gas), which satisfies the scalar-advection equation. The geometrical features of the interface such as its unit vector normal
$c = 0$ in gas), which satisfies the scalar-advection equation. The geometrical features of the interface such as its unit vector normal ![]() $\boldsymbol {\hat {n}}$ and the curvature
$\boldsymbol {\hat {n}}$ and the curvature ![]() $\kappa$ (
$\kappa$ (![]() $= \boldsymbol {\nabla }\boldsymbol {\cdot }\hat {\boldsymbol {n}}$) are calculated using the height-function method (Popinet Reference Popinet2009, Reference Popinet2018). The governing equations for the gas and the fluid are solved using a one-fluid approximation (Prosperetti & Tryggvason Reference Prosperetti and Tryggvason2009; Tryggvason, Scardovelli & Zaleski Reference Tryggvason, Scardovelli and Zaleski2011), where the singular surface tension is approximated as
$= \boldsymbol {\nabla }\boldsymbol {\cdot }\hat {\boldsymbol {n}}$) are calculated using the height-function method (Popinet Reference Popinet2009, Reference Popinet2018). The governing equations for the gas and the fluid are solved using a one-fluid approximation (Prosperetti & Tryggvason Reference Prosperetti and Tryggvason2009; Tryggvason, Scardovelli & Zaleski Reference Tryggvason, Scardovelli and Zaleski2011), where the singular surface tension is approximated as ![]() $\boldsymbol {f}_\gamma = \kappa \delta _s\boldsymbol {\hat {n}} \approx \kappa \boldsymbol {\nabla }c$ (Brackbill, Kothe & Zemach Reference Brackbill, Kothe and Zemach1992). Note that the time step in our simulations is restricted by the oscillation period of the smallest wavelength of the capillary wave because the surface tension scheme is explicit in time (Popinet Reference Popinet2009; Popinet & Collaborators Reference Popinet2024).
$\boldsymbol {f}_\gamma = \kappa \delta _s\boldsymbol {\hat {n}} \approx \kappa \boldsymbol {\nabla }c$ (Brackbill, Kothe & Zemach Reference Brackbill, Kothe and Zemach1992). Note that the time step in our simulations is restricted by the oscillation period of the smallest wavelength of the capillary wave because the surface tension scheme is explicit in time (Popinet Reference Popinet2009; Popinet & Collaborators Reference Popinet2024).
Utilizing the AMR feature of Basilisk C, the errors in the volume of fluid tracer and interface curvature are minimized by applying a tolerance threshold of ![]() $10^{-3}$ and
$10^{-3}$ and ![]() $10^{-4}$, respectively. In addition, the refinement of the grid is also performed based on the velocity (tolerance threshold,
$10^{-4}$, respectively. In addition, the refinement of the grid is also performed based on the velocity (tolerance threshold, ![]() $10^{-2}$), conformation tensor
$10^{-2}$), conformation tensor ![]() $\boldsymbol {A}$ (tolerance threshold,
$\boldsymbol {A}$ (tolerance threshold, ![]() $10^{-2}$) and yielded region identified by
$10^{-2}$) and yielded region identified by ![]() $K$ (tolerance threshold,
$K$ (tolerance threshold, ![]() $10^{-3}$) to accurately resolve the regions of low strain rates and elastic deformation. These tolerance threshold values can be interpreted as the maximum error associated with the subsequent application of volume-averaged downsampling of fine-resolution-solution and bilinear upscaling of coarse-level-solution (Popinet Reference Popinet2015; van Hooft et al. Reference van Hooft, Popinet, van Heerwaarden, van der Linden, de Roode and van de Wiel2018). We highlight that these refinements offer the advantage of an almost uniform grid in key regions of interest (see also van Hooft (Reference van Hooft2019)) and acknowledge that the efficacy of such refinement criteria as employed in this study needs further investigation. For AMR, we employ a grid resolution ensuring a minimum cell size of
$10^{-3}$) to accurately resolve the regions of low strain rates and elastic deformation. These tolerance threshold values can be interpreted as the maximum error associated with the subsequent application of volume-averaged downsampling of fine-resolution-solution and bilinear upscaling of coarse-level-solution (Popinet Reference Popinet2015; van Hooft et al. Reference van Hooft, Popinet, van Heerwaarden, van der Linden, de Roode and van de Wiel2018). We highlight that these refinements offer the advantage of an almost uniform grid in key regions of interest (see also van Hooft (Reference van Hooft2019)) and acknowledge that the efficacy of such refinement criteria as employed in this study needs further investigation. For AMR, we employ a grid resolution ensuring a minimum cell size of ![]() $\varDelta = R_0/1024$, corresponding to 1024 cells across the initial bubble radius. However, when
$\varDelta = R_0/1024$, corresponding to 1024 cells across the initial bubble radius. However, when ![]() ${{\textit {De}}} \ge 1$, we switch to
${{\textit {De}}} \ge 1$, we switch to ![]() $\varDelta = R_0/2048$. Comprehensive grid-independence studies were conducted to confirm that the results remain unaffected by the chosen grid size (see Appendix C). We consider a square domain measuring
$\varDelta = R_0/2048$. Comprehensive grid-independence studies were conducted to confirm that the results remain unaffected by the chosen grid size (see Appendix C). We consider a square domain measuring ![]() $8R_0$ on each side, representing only one slice of the three-dimensional bursting bubble process leveraging the axisymmetric flow assumption. For both liquid and gas, free-slip and no-penetration boundary conditions are applied at the domain boundaries, while a zero-gradient condition is used for pressure. To ensure that ejected droplets, which arise from the breakup of the Worthington jet, can leave the domain, an outflow boundary condition is employed at the top boundary. The chosen domain size ensures that the boundaries do not influence the bubble-bursting process. Lastly, the solution of the constitutive relations ((2.8)–(2.9)) require the log-conformation approach proposed by Fattal & Kupferman (Reference Fattal and Kupferman2004) (also see López-Herrera, Popinet & Castrejón-Pita (Reference López-Herrera, Popinet and Castrejón-Pita2019), Dixit et al. (Reference Dixit, Oratis, Zinelis, Lohse and Sanjay2024) and França et al. (Reference França, Jalaal and Oishi2024); and Appendix B). For details of our implementation in Basilisk C, we refer the readers to Balasubramanian (Reference Balasubramanian2023).
$8R_0$ on each side, representing only one slice of the three-dimensional bursting bubble process leveraging the axisymmetric flow assumption. For both liquid and gas, free-slip and no-penetration boundary conditions are applied at the domain boundaries, while a zero-gradient condition is used for pressure. To ensure that ejected droplets, which arise from the breakup of the Worthington jet, can leave the domain, an outflow boundary condition is employed at the top boundary. The chosen domain size ensures that the boundaries do not influence the bubble-bursting process. Lastly, the solution of the constitutive relations ((2.8)–(2.9)) require the log-conformation approach proposed by Fattal & Kupferman (Reference Fattal and Kupferman2004) (also see López-Herrera, Popinet & Castrejón-Pita (Reference López-Herrera, Popinet and Castrejón-Pita2019), Dixit et al. (Reference Dixit, Oratis, Zinelis, Lohse and Sanjay2024) and França et al. (Reference França, Jalaal and Oishi2024); and Appendix B). For details of our implementation in Basilisk C, we refer the readers to Balasubramanian (Reference Balasubramanian2023).
2.3. Initial condition
The initial shape of the bubble is obtained by solving the Young–Laplace equations to find the quasistatic equilibrium state for a specified Bond number, ![]() ${\textit {Bo}}$ (see Lhuissier & Villermaux Reference Lhuissier and Villermaux2012; Deike et al. Reference Deike, Ghabache, Liger-Belair, Das, Zaleski, Popinet and Séon2018; Sanjay et al. Reference Sanjay, Lohse and Jalaal2021). In this study, we focus more on the capillary effects than gravitational effects, and hence the value of
${\textit {Bo}}$ (see Lhuissier & Villermaux Reference Lhuissier and Villermaux2012; Deike et al. Reference Deike, Ghabache, Liger-Belair, Das, Zaleski, Popinet and Séon2018; Sanjay et al. Reference Sanjay, Lohse and Jalaal2021). In this study, we focus more on the capillary effects than gravitational effects, and hence the value of ![]() $\mathcal {B}$o is set to
$\mathcal {B}$o is set to ![]() $10^{-3}$. At low values of
$10^{-3}$. At low values of ![]() $\mathcal {B}$o, the initial shape of the bubble closely approximates a sphere within the surrounding Newtonian medium. However, for the EVP medium considered in this study, we make a significant assumption by retaining the spherical bubble shape. It is important to note that this assumption is a crucial aspect of our investigation. Given the EVP behaviour of the liquid medium in our work, the bubble shape close to the fluid–air interface would exhibit a different interface profile than that in the Newtonian medium. The shapes of the bubble rising in an EVP medium constitute an active area of research (see Izbassarov et al. Reference Izbassarov, Rosti, Ardekani, Sarabian, Hormozi, Brandt and Tammisola2018; Lopez, Naccache & de Souza Mendes Reference Lopez, Naccache and de Souza Mendes2018; Moschopoulos et al. Reference Moschopoulos, Spyridakis, Varchanis, Dimakopoulos and Tsamopoulos2021).
$\mathcal {B}$o, the initial shape of the bubble closely approximates a sphere within the surrounding Newtonian medium. However, for the EVP medium considered in this study, we make a significant assumption by retaining the spherical bubble shape. It is important to note that this assumption is a crucial aspect of our investigation. Given the EVP behaviour of the liquid medium in our work, the bubble shape close to the fluid–air interface would exhibit a different interface profile than that in the Newtonian medium. The shapes of the bubble rising in an EVP medium constitute an active area of research (see Izbassarov et al. Reference Izbassarov, Rosti, Ardekani, Sarabian, Hormozi, Brandt and Tammisola2018; Lopez, Naccache & de Souza Mendes Reference Lopez, Naccache and de Souza Mendes2018; Moschopoulos et al. Reference Moschopoulos, Spyridakis, Varchanis, Dimakopoulos and Tsamopoulos2021).
Further, the bubble's shape at the fluid–air interface depends not only on the material behaviour of the surrounding medium in which the bubble rises but also on the generation and dynamics before reaching the free surface. The bubble rise depends on the buoyancy forces, which should be strong enough to yield the EVP medium. Hence, one might expect a non-trivial shape as suggested by Lopez et al. (Reference Lopez, Naccache and de Souza Mendes2018) and Deoclecio, Soares & Popinet (Reference Deoclecio, Soares and Popinet2023). However, in the present study, we consider the small spherical bubbles trapped at the interface rather than rising bubbles reaching the free surface to be consistent with the previous investigations. It should be pointed out that the bubble cap breakup is also sensitive to the employed numerical method. For a comparative analysis to understand the transient effects of elasticity on the bubble bursting in an EVP medium, we consider the same initial condition as employed by Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021) for the case of bubble bursting in a viscoplastic medium. Hence, an initial stress-free condition is employed in the present computations, which would otherwise correspond to some presheared state if the bubble rose close to the free surface and burst instantly.
The bubble-bursting problem could also be coupled with the bubble rise in an EVP medium with a free surface to obtain a more realistic initial condition. However, such a coupling is limited by the numerical methodology to treat the breakup of bubble cap ![]() $\delta$ (as the thin initial film between the bubble and air drains). Moreover, the bubbles usually sit on the free surface before the cap bursts (Bartlett et al. Reference Bartlett, Oratis, Santin and Bird2023), allowing enough time for the elastic stresses to relax if the drainage time is much longer than the relaxation time. Hence, as a simplification in this work, the open cavity is considered as the initial condition, as shown in figure 1. In this figure,
$\delta$ (as the thin initial film between the bubble and air drains). Moreover, the bubbles usually sit on the free surface before the cap bursts (Bartlett et al. Reference Bartlett, Oratis, Santin and Bird2023), allowing enough time for the elastic stresses to relax if the drainage time is much longer than the relaxation time. Hence, as a simplification in this work, the open cavity is considered as the initial condition, as shown in figure 1. In this figure, ![]() $(\mathcal {R},\mathcal {Z})$ represent the radial and axial coordinate system, and
$(\mathcal {R},\mathcal {Z})$ represent the radial and axial coordinate system, and ![]() $\mathcal {H}_i \approx 2$ denotes the initial bubble depth, while
$\mathcal {H}_i \approx 2$ denotes the initial bubble depth, while ![]() $\theta _i$ indicates the initial location of the cavity-free surface intersection. We incorporate a finite curvature
$\theta _i$ indicates the initial location of the cavity-free surface intersection. We incorporate a finite curvature ![]() $\kappa _0=100$ at the intersection of bubble and free surface to regularize the curvature singularity, consistent with Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021), which has been demonstrated to have no significant influence on the bubble-bursting dynamics.
$\kappa _0=100$ at the intersection of bubble and free surface to regularize the curvature singularity, consistent with Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021), which has been demonstrated to have no significant influence on the bubble-bursting dynamics.
3. Results
3.1. Validation
This section compares our results with Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021), who used a regularized Bingham model to study bubble bursting in a viscoplastic medium. In such a viscoplastic model, the fluid features a rigid body motion (![]() $\boldsymbol {\mathcal {D}} = \boldsymbol {0}$) below the yield stress and flows like a viscous liquid above the yield stress. The EVP model used in this work ((2.4) and (2.15)) reduces to the Bingham model if
$\boldsymbol {\mathcal {D}} = \boldsymbol {0}$) below the yield stress and flows like a viscous liquid above the yield stress. The EVP model used in this work ((2.4) and (2.15)) reduces to the Bingham model if ![]() ${{\textit {De}}} = 0$ and
${{\textit {De}}} = 0$ and ![]() ${{\textit {Oh}}}_s = 0$ (see also Appendix D), giving
${{\textit {Oh}}}_s = 0$ (see also Appendix D), giving
where ![]() $({{\textit {Oh}}}_s + {{\textit {Oh}}}_p/K) = {{\textit {Oh}}}_p/K$ is the apparent viscosity. Figures 2 and 3 illustrate the comparison between Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021) and our simulations with
$({{\textit {Oh}}}_s + {{\textit {Oh}}}_p/K) = {{\textit {Oh}}}_p/K$ is the apparent viscosity. Figures 2 and 3 illustrate the comparison between Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021) and our simulations with ![]() ${{\textit {De}}}=10^{-4}$,
${{\textit {De}}}=10^{-4}$, ![]() ${{\textit {Oh}}}_p = 9.5 \times 10^{-3}$ and
${{\textit {Oh}}}_p = 9.5 \times 10^{-3}$ and ![]() ${{\textit {Oh}}}_s=5\times 10^{-4}$. For a low plastocapillary number (
${{\textit {Oh}}}_s=5\times 10^{-4}$. For a low plastocapillary number (![]() $\mathcal {J} = 0.1$), the capillary waves meet at the bottom of the bubble cavity, leading to an inertial flow-focusing that forms a Worthington jet, which subsequently breaks into droplets (figure 2a).
$\mathcal {J} = 0.1$), the capillary waves meet at the bottom of the bubble cavity, leading to an inertial flow-focusing that forms a Worthington jet, which subsequently breaks into droplets (figure 2a).
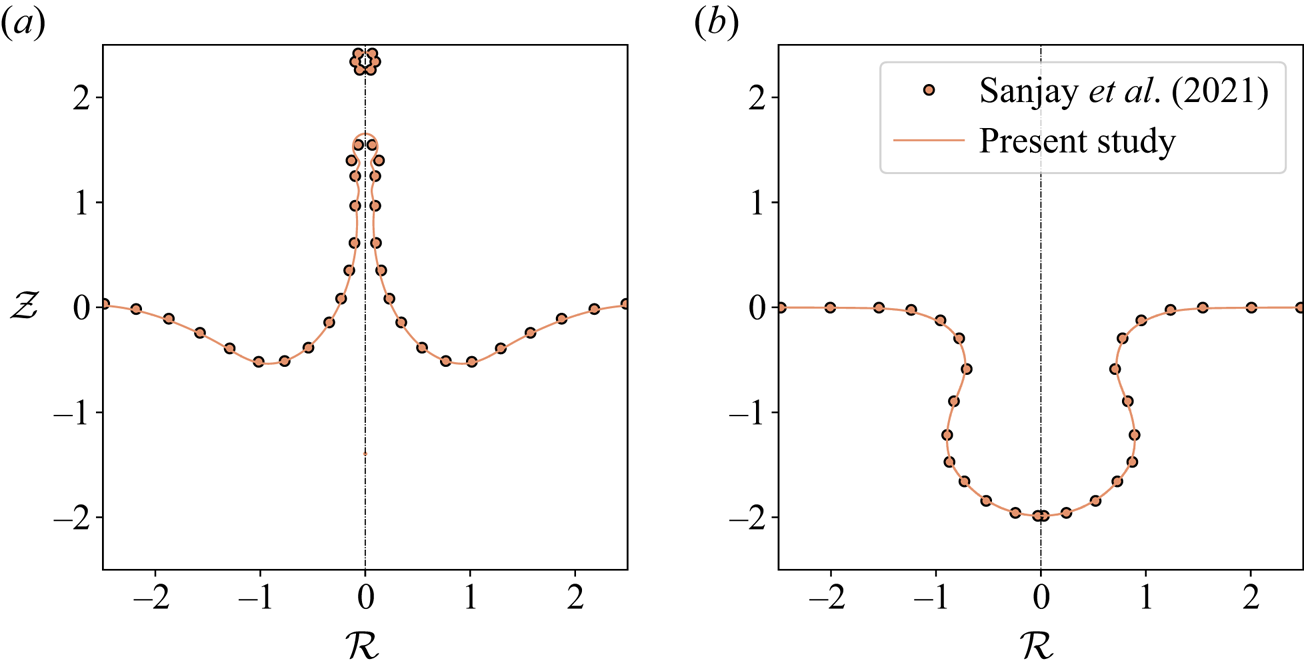
Figure 2. Validation of interface shapes obtained with EVP fluid at very low Deborah number of ![]() ${{\textit {De}}}=10^{-4}$ against the results obtained by Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021) with viscoplastic fluid at (a)
${{\textit {De}}}=10^{-4}$ against the results obtained by Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021) with viscoplastic fluid at (a) ![]() $t=1.0,\mathcal {J}=0.1$ and (b)
$t=1.0,\mathcal {J}=0.1$ and (b) ![]() $t=0.75,\mathcal {J}=1.0$.
$t=0.75,\mathcal {J}=1.0$.

Figure 3. Comparison of the deformation-rate tensor obtained with (a i) viscoplastic fluid by Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021) and (a ii) EVP fluid at ![]() $\mathcal {J} = 1.0,{{\textit {De}}}=10^{-4}$ at
$\mathcal {J} = 1.0,{{\textit {De}}}=10^{-4}$ at ![]() $t=1.0$. Time evolution of deformation tensor in EVP fluid at (b i)
$t=1.0$. Time evolution of deformation tensor in EVP fluid at (b i) ![]() $t=1.0$ and (b ii)
$t=1.0$ and (b ii) ![]() $t=1.6$ for
$t=1.6$ for ![]() $\mathcal {J} = 1.0,{{\textit {De}}}=10^{-4}$.
$\mathcal {J} = 1.0,{{\textit {De}}}=10^{-4}$.
On the other hand, at high ![]() $\mathcal {J}$ (i.e. at
$\mathcal {J}$ (i.e. at ![]() $\mathcal {J} = 1$), at comparable time scales between the two models, the bubble cavities are identical (figures 2b and 3a). Nonetheless, the two cases show different
$\mathcal {J} = 1$), at comparable time scales between the two models, the bubble cavities are identical (figures 2b and 3a). Nonetheless, the two cases show different ![]() $\|\boldsymbol {\mathcal {D}}\|$. This apparent discrepancy can be attributed to the different behaviours of the unyielded region in the Bingham viscoplastic and the Saramito (Reference Saramito2007) EVP models. Notably, in the case of the regularized Bingham model employed for simulating bubble bursting in viscoplastic fluid by Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021), at the stoppage time, the entire medium is unyielded (
$\|\boldsymbol {\mathcal {D}}\|$. This apparent discrepancy can be attributed to the different behaviours of the unyielded region in the Bingham viscoplastic and the Saramito (Reference Saramito2007) EVP models. Notably, in the case of the regularized Bingham model employed for simulating bubble bursting in viscoplastic fluid by Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021), at the stoppage time, the entire medium is unyielded (![]() $K \approx 0$ throughout the bulk) and the fluid flow ceases due to stresses falling below the yield stress. Consequently, the deformation tensor
$K \approx 0$ throughout the bulk) and the fluid flow ceases due to stresses falling below the yield stress. Consequently, the deformation tensor ![]() $\|\boldsymbol {\mathcal {D}}\|$ is zero (rigid body rotation or no flow). For the EVP model, nearly the entire liquid remains unyielded as regions with
$\|\boldsymbol {\mathcal {D}}\|$ is zero (rigid body rotation or no flow). For the EVP model, nearly the entire liquid remains unyielded as regions with ![]() $K \neq 0$ are predominantly situated close to the fluid interface. However, the bulk exhibits a Kelvin–Voigt viscoelastic solid behaviour (
$K \neq 0$ are predominantly situated close to the fluid interface. However, the bulk exhibits a Kelvin–Voigt viscoelastic solid behaviour (![]() $\boldsymbol {\overset {\nabla }{A}} = \boldsymbol {0}$ and
$\boldsymbol {\overset {\nabla }{A}} = \boldsymbol {0}$ and ![]() $\boldsymbol {\tau _p} = Ec(\boldsymbol {A} - \boldsymbol {I})$, see Saramito Reference Saramito2007). Consequently, even below the yield stress, the deformation tensor
$\boldsymbol {\tau _p} = Ec(\boldsymbol {A} - \boldsymbol {I})$, see Saramito Reference Saramito2007). Consequently, even below the yield stress, the deformation tensor ![]() $\|\boldsymbol {\mathcal {D}}\|$ can be non-zero. Note that, for the Kelvin–Voigt viscoelastic rigid body motion (
$\|\boldsymbol {\mathcal {D}}\|$ can be non-zero. Note that, for the Kelvin–Voigt viscoelastic rigid body motion (![]() $\|\boldsymbol {\mathcal {D}}\| = 0$) occurs in the limit of very large elastic modulus (i.e.
$\|\boldsymbol {\mathcal {D}}\| = 0$) occurs in the limit of very large elastic modulus (i.e. ![]() $Ec = {{\textit {Oh}}}_p/{{\textit {De}}} \to \infty$). The simulations are stopped at
$Ec = {{\textit {Oh}}}_p/{{\textit {De}}} \to \infty$). The simulations are stopped at ![]() $t=2$ and the final interface shape of the bubble, where the extra stress balances the capillary stress, are not investigated in this study.
$t=2$ and the final interface shape of the bubble, where the extra stress balances the capillary stress, are not investigated in this study.
3.2. Regime map
We investigate the dynamics of bubble bursting in an EVP medium by exploring the influence of elastic stress relaxation and yield stress, quantified by the Deborah ![]() ${{\textit {De}}}$ and the plastocapillary
${{\textit {De}}}$ and the plastocapillary ![]() $\mathcal {J}$ numbers, respectively (see França et al. Reference França, Jalaal and Oishi2024). Our exploration spans a parameter space with
$\mathcal {J}$ numbers, respectively (see França et al. Reference França, Jalaal and Oishi2024). Our exploration spans a parameter space with ![]() ${{\textit {De}}}\in [10^{-3},20]$ and
${{\textit {De}}}\in [10^{-3},20]$ and ![]() $\mathcal {J} \in [10^{-2},1]$ while maintaining a fixed Ohnesorge number of
$\mathcal {J} \in [10^{-2},1]$ while maintaining a fixed Ohnesorge number of ![]() ${{\textit {Oh}}}=10^{-2}$,
${{\textit {Oh}}}=10^{-2}$, ![]() $\beta$ of 0.5 and Bond number of
$\beta$ of 0.5 and Bond number of ![]() ${\textit {Bo}}=10^{-3}$. The value of
${\textit {Bo}}=10^{-3}$. The value of ![]() ${{\textit {Oh}}}_s = {{\textit {Oh}}}_p = 0.005$ (which fixes
${{\textit {Oh}}}_s = {{\textit {Oh}}}_p = 0.005$ (which fixes ![]() $\beta$ at 0.5) is applicable for all the discussions except for § 3.6 (see § 3.6 to identify the variation of regime map with
$\beta$ at 0.5) is applicable for all the discussions except for § 3.6 (see § 3.6 to identify the variation of regime map with ![]() $\beta$). All the simulations were carried out until
$\beta$). All the simulations were carried out until ![]() $t\ge 1.2$, as this time was seen to be sufficient to capture the key dynamics of the bursting process. This investigation leads us to a regime map, presented in figure 4. We identify four distinct regimes, namely (i) droplet formation from the tip of the Worthington jet (Droplet–A), (ii) no Worthington jet formation, (iii) no pinch-off of the Worthington jet and no droplet, (iv) pinch-off at the base of the Worthington jet to form a droplet (Droplet–B). Note that in the context of this study, we characterize a jet formed by inertial flow-focusing as the Worthington jet if it crosses the equilibrium surface
$t\ge 1.2$, as this time was seen to be sufficient to capture the key dynamics of the bursting process. This investigation leads us to a regime map, presented in figure 4. We identify four distinct regimes, namely (i) droplet formation from the tip of the Worthington jet (Droplet–A), (ii) no Worthington jet formation, (iii) no pinch-off of the Worthington jet and no droplet, (iv) pinch-off at the base of the Worthington jet to form a droplet (Droplet–B). Note that in the context of this study, we characterize a jet formed by inertial flow-focusing as the Worthington jet if it crosses the equilibrium surface ![]() $\mathcal {Z}=0$ at the axis
$\mathcal {Z}=0$ at the axis ![]() $(\mathcal {R}=0)$.
$(\mathcal {R}=0)$.

Figure 4. Regime map in terms of the plastocapillarity number ![]() $\mathcal {J}$ and the Deborah number
$\mathcal {J}$ and the Deborah number ![]() ${{\textit {De}}}$, distinguishing the droplet formation (Droplet–I), no jet formation, jet pinch-off (Droplet–II) and no-pinch-off regimes. All the cases correspond to
${{\textit {De}}}$, distinguishing the droplet formation (Droplet–I), no jet formation, jet pinch-off (Droplet–II) and no-pinch-off regimes. All the cases correspond to ![]() ${{\textit {Oh}}}_s = {{\textit {Oh}}}_p = 0.005$. The four series of insets illustrate typical cases in these regimes, namely (b)
${{\textit {Oh}}}_s = {{\textit {Oh}}}_p = 0.005$. The four series of insets illustrate typical cases in these regimes, namely (b) ![]() $(\mathcal {J}, {{\textit {De}}}) = (0.1, 20)$, (c) (0.01, 0.01), (d) (0.8, 0.1) and (e) (1, 2). Different markers identify the viscoelastic limit corresponding to
$(\mathcal {J}, {{\textit {De}}}) = (0.1, 20)$, (c) (0.01, 0.01), (d) (0.8, 0.1) and (e) (1, 2). Different markers identify the viscoelastic limit corresponding to ![]() $\mathcal {J}=0$.
$\mathcal {J}=0$.
3.2.1. Droplet formation regime, Droplet–A (low elastic stress relaxation time and yield-stress limit,  $\mathcal {J} \rightarrow 0,\,{{\textit {De}}}\rightarrow 0$)
$\mathcal {J} \rightarrow 0,\,{{\textit {De}}}\rightarrow 0$)
For small Deborah and plastocapillary numbers (![]() ${{\textit {De}}} \le 0.05$ and
${{\textit {De}}} \le 0.05$ and ![]() $\mathcal {J} \le 0.4$), we observe a Newtonian-like behaviour where the initial capillary waves collapse at the bottom of the bubble cavity resulting in a Worthington jet formation (Gordillo & Blanco-Rodríguez Reference Gordillo and Blanco-Rodríguez2023; Dixit et al. Reference Dixit, Oratis, Zinelis, Lohse and Sanjay2024). Further, due to the higher capillary forces compared with the viscous and elastic forces, the jet breaks up, resulting in droplets (Walls et al. Reference Walls, Henaux and Bird2015). This regime often features multiple drops similar to the case of the Newtonian bubble-bursting process (Berny et al. Reference Berny, Deike, Séon and Popinet2020).
$\mathcal {J} \le 0.4$), we observe a Newtonian-like behaviour where the initial capillary waves collapse at the bottom of the bubble cavity resulting in a Worthington jet formation (Gordillo & Blanco-Rodríguez Reference Gordillo and Blanco-Rodríguez2023; Dixit et al. Reference Dixit, Oratis, Zinelis, Lohse and Sanjay2024). Further, due to the higher capillary forces compared with the viscous and elastic forces, the jet breaks up, resulting in droplets (Walls et al. Reference Walls, Henaux and Bird2015). This regime often features multiple drops similar to the case of the Newtonian bubble-bursting process (Berny et al. Reference Berny, Deike, Séon and Popinet2020).
For the viscoplastic fluid, Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021) had identified this regime to fall below ![]() $\mathcal {J} \approx 0.3$ for small
$\mathcal {J} \approx 0.3$ for small ![]() ${{\textit {Oh}}}$ and
${{\textit {Oh}}}$ and ![]() ${{\textit {De}}} = 0$, beyond which the jet breakup is suppressed owing to an increase in the apparent viscosity which critically dampens the capillary waves. Figure 4 identifies this transition at
${{\textit {De}}} = 0$, beyond which the jet breakup is suppressed owing to an increase in the apparent viscosity which critically dampens the capillary waves. Figure 4 identifies this transition at ![]() $\mathcal {J} \approx 0.5$ for
$\mathcal {J} \approx 0.5$ for ![]() ${{\textit {De}}} \to 0$. This delayed droplet–no-droplet transition is attributed to a reduction in the effective viscosity of the EVP matrix in comparison with the purely Bingham fluid (refer to Appendix D). The effective viscosity in the limit of vanishing
${{\textit {De}}} \to 0$. This delayed droplet–no-droplet transition is attributed to a reduction in the effective viscosity of the EVP matrix in comparison with the purely Bingham fluid (refer to Appendix D). The effective viscosity in the limit of vanishing ![]() ${{\textit {De}}}$ is
${{\textit {De}}}$ is ![]() ${{\textit {Oh}}}_p/K$ contrary to
${{\textit {Oh}}}_p/K$ contrary to ![]() ${{\textit {Oh}}}/K$ for a purely Bingham fluid (Sanjay et al. Reference Sanjay, Lohse and Jalaal2021). This delay in stress relaxation delays the transition to the plastic behaviour within the EVP matrix. Consequently, at finite
${{\textit {Oh}}}/K$ for a purely Bingham fluid (Sanjay et al. Reference Sanjay, Lohse and Jalaal2021). This delay in stress relaxation delays the transition to the plastic behaviour within the EVP matrix. Consequently, at finite ![]() ${{\textit {De}}}$, a critical increase in the apparent viscosity occurs at a higher value of
${{\textit {De}}}$, a critical increase in the apparent viscosity occurs at a higher value of ![]() $\mathcal {J}$.
$\mathcal {J}$.
Furthermore, as ![]() ${{\textit {De}}}$ increases further, even for low
${{\textit {De}}}$ increases further, even for low ![]() $\mathcal {J}$, jet breakup into droplets is suppressed. This observation agrees with that of Rodríguez-Díaz et al. (Reference Rodríguez-Díaz, Rubio, Montanero, Gañán-Calvo and Cabezas2023) and Dixit et al. (Reference Dixit, Oratis, Zinelis, Lohse and Sanjay2024): adding polymers hinders droplet ejection even for the small solvent-to-polymer viscosity ratio. We attribute this observation to a delay in elastic stress relaxation at higher
$\mathcal {J}$, jet breakup into droplets is suppressed. This observation agrees with that of Rodríguez-Díaz et al. (Reference Rodríguez-Díaz, Rubio, Montanero, Gañán-Calvo and Cabezas2023) and Dixit et al. (Reference Dixit, Oratis, Zinelis, Lohse and Sanjay2024): adding polymers hinders droplet ejection even for the small solvent-to-polymer viscosity ratio. We attribute this observation to a delay in elastic stress relaxation at higher ![]() ${{\textit {De}}}$, increasing the elastic stresses that counteract capillarity to prevent both the end-pinching and Rayleigh–Plateau instabilities (Pandey et al. Reference Pandey, Kansal, Herrada, Eggers and Snoeijer2021).
${{\textit {De}}}$, increasing the elastic stresses that counteract capillarity to prevent both the end-pinching and Rayleigh–Plateau instabilities (Pandey et al. Reference Pandey, Kansal, Herrada, Eggers and Snoeijer2021).
3.2.2. No-jet regime (viscoplastic limit,  $\mathcal {J} \gg 0,\,{{\textit {De}}}\rightarrow 0$)
$\mathcal {J} \gg 0,\,{{\textit {De}}}\rightarrow 0$)
In the case of a purely viscoplastic fluid, Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021) observed that for ![]() $\mathcal {J} \ge 0.65$, the surface tension fails to yield the entire cavity, and the capillary wave freezes before reaching the bottom of the cavity, leading to a non-flat final equilibrium shape. In this work, the no jet regime commences at
$\mathcal {J} \ge 0.65$, the surface tension fails to yield the entire cavity, and the capillary wave freezes before reaching the bottom of the cavity, leading to a non-flat final equilibrium shape. In this work, the no jet regime commences at ![]() $\mathcal {J} \approx 0.7$ in the limit of
$\mathcal {J} \approx 0.7$ in the limit of ![]() ${{\textit {De}}} \to 0$, characterized by the absence of a jet crossing the free surface (
${{\textit {De}}} \to 0$, characterized by the absence of a jet crossing the free surface (![]() $\mathcal {Z} = 0$). This finding aligns with the increased plasticity effect at higher
$\mathcal {Z} = 0$). This finding aligns with the increased plasticity effect at higher ![]() $\mathcal {J}$.
$\mathcal {J}$.
However, our results diverge from the case of a purely viscoplastic fluid in one critical aspect: we find that despite the increasing plasticity, the bubble cavity consistently yields, albeit slowly. In the context of purely viscoplastic fluids, the yield surface is stationary and aligns with the cavity boundary, resulting in a zero deformation rate (![]() $\|\boldsymbol {\mathcal {D}}\| = 0$), independent of resultant stress fields that are below the yield stress. However, under EVP conditions, the medium behaves akin to a Kelvin–Voigt solid below the yield stress, leading to a slow deformation of the cavity over extended time scales depending on the elastocapillary number
$\|\boldsymbol {\mathcal {D}}\| = 0$), independent of resultant stress fields that are below the yield stress. However, under EVP conditions, the medium behaves akin to a Kelvin–Voigt solid below the yield stress, leading to a slow deformation of the cavity over extended time scales depending on the elastocapillary number ![]() $Ec = {{\textit {Oh}}}_p/{{\textit {De}}} = (1-\beta ) {{\textit {Oh}}}/{{\textit {De}}}$, as indicated by a non-zero deformation rate (
$Ec = {{\textit {Oh}}}_p/{{\textit {De}}} = (1-\beta ) {{\textit {Oh}}}/{{\textit {De}}}$, as indicated by a non-zero deformation rate (![]() $\|\boldsymbol {\mathcal {D}}\| \ne 0$, see § 3.1). For an infinite
$\|\boldsymbol {\mathcal {D}}\| \ne 0$, see § 3.1). For an infinite ![]() $Ec$, a rigid body motion of the unyielded region is recovered.
$Ec$, a rigid body motion of the unyielded region is recovered.
3.2.3. No pinch-off regime (viscoelastocapillary limit,  ${{\textit {De}}} \sim O(1)$)
${{\textit {De}}} \sim O(1)$)
At large values of ![]() $\mathcal {J}$, as we increase the Deborah number (
$\mathcal {J}$, as we increase the Deborah number (![]() ${{\textit {De}}} \sim O(1)$), we notice that a Worthington jet forms irrespective of
${{\textit {De}}} \sim O(1)$), we notice that a Worthington jet forms irrespective of ![]() $\mathcal {J}$. This
$\mathcal {J}$. This ![]() $\mathcal {J}$–independent behaviour is due to a decrease in the elastocapillary number
$\mathcal {J}$–independent behaviour is due to a decrease in the elastocapillary number ![]() $Ec = {{\textit {Oh}}}_p/{{\textit {De}}} = (1-\beta ) {{\textit {Oh}}}/{{\textit {De}}}$ with an increase in
$Ec = {{\textit {Oh}}}_p/{{\textit {De}}} = (1-\beta ) {{\textit {Oh}}}/{{\textit {De}}}$ with an increase in ![]() ${{\textit {De}}}$ at fixed
${{\textit {De}}}$ at fixed ![]() ${{\textit {Oh}}}_p$. Consequently, for a considered deformation of the EVP matrix the maximum elastic energy decreases with
${{\textit {Oh}}}_p$. Consequently, for a considered deformation of the EVP matrix the maximum elastic energy decreases with ![]() ${{\textit {De}}}$ at fixed
${{\textit {De}}}$ at fixed ![]() ${{\textit {Oh}}}_p$ (refer to figure 19c), leading to the formation of the jet. This jet development is significantly influenced by the variations in the ratio of polymer to total viscosity (
${{\textit {Oh}}}_p$ (refer to figure 19c), leading to the formation of the jet. This jet development is significantly influenced by the variations in the ratio of polymer to total viscosity (![]() $\beta$, see § 3.6), which modifies the elastocapillary number at fixed
$\beta$, see § 3.6), which modifies the elastocapillary number at fixed ![]() ${{\textit {Oh}}}$ and
${{\textit {Oh}}}$ and ![]() ${{\textit {De}}}$. Nonetheless, the elastic forces still dominate over capillary, resulting in the prevention of droplet formation from the jet even at small
${{\textit {De}}}$. Nonetheless, the elastic forces still dominate over capillary, resulting in the prevention of droplet formation from the jet even at small ![]() $\mathcal {J}$ (see § 3.2.1). The role of elastocapillary number in jet formation is further explained in 3.3.
$\mathcal {J}$ (see § 3.2.1). The role of elastocapillary number in jet formation is further explained in 3.3.
3.2.4. Droplet formation regime, Droplet–B (Newtonian-like limit,  ${{\textit {De}}}\gg 1$)
${{\textit {De}}}\gg 1$)
For very high values of Deborah numbers (![]() ${{\textit {De}}} \gg 1$), the bursting bubble dynamics appear to be independent of
${{\textit {De}}} \gg 1$), the bursting bubble dynamics appear to be independent of ![]() $\mathcal {J}$. However, in contrast to the ‘no pinch-off of the Worthington jet and no droplet regime’, the Worthington jet breaks up at the base to form one droplet. In this regime, the yield surface is still very close to the liquid–gas interface (refer to figure 5d and 7c), and most of the EVP fluid remains unyielded. At such high values of
$\mathcal {J}$. However, in contrast to the ‘no pinch-off of the Worthington jet and no droplet regime’, the Worthington jet breaks up at the base to form one droplet. In this regime, the yield surface is still very close to the liquid–gas interface (refer to figure 5d and 7c), and most of the EVP fluid remains unyielded. At such high values of ![]() ${{\textit {De}}}$, the elastocapillary number becomes too small, and the elastic stresses fail to prevent either the formation of the Worthington jet or its subsequent breakup at the base. Such a Newtonian-like regime with vanishing elastic stresses was also found by França et al. (Reference França, Jalaal and Oishi2024).
${{\textit {De}}}$, the elastocapillary number becomes too small, and the elastic stresses fail to prevent either the formation of the Worthington jet or its subsequent breakup at the base. Such a Newtonian-like regime with vanishing elastic stresses was also found by França et al. (Reference França, Jalaal and Oishi2024).

Figure 5. Variation of the dynamics of bubble bursting in (a) a Newtonian medium compared with EVP medium for ![]() $\mathcal {J}=0.1$,
$\mathcal {J}=0.1$, ![]() ${{\textit {Oh}}}=10^{-2}$ at (b)
${{\textit {Oh}}}=10^{-2}$ at (b) ![]() ${{\textit {De}}}=0.02$, (c)
${{\textit {De}}}=0.02$, (c) ![]() ${{\textit {De}}}=1$, (d)
${{\textit {De}}}=1$, (d) ![]() ${{\textit {De}}}=20$. The left-hand part of each subpanel shows the flow topology parameter
${{\textit {De}}}=20$. The left-hand part of each subpanel shows the flow topology parameter ![]() $\mathcal {Q}$ and the right-hand part of the subpanel shows the trace of elastic stress on a
$\mathcal {Q}$ and the right-hand part of the subpanel shows the trace of elastic stress on a ![]() $\log _{10}$ scale. The yielded regions are marked by a grey line, which corresponds to
$\log _{10}$ scale. The yielded regions are marked by a grey line, which corresponds to ![]() $\mathcal {J}\approxeq \|\boldsymbol {\tau _d}\|$. For the Newtonian medium, both subpanels show the flow topology parameter.
$\mathcal {J}\approxeq \|\boldsymbol {\tau _d}\|$. For the Newtonian medium, both subpanels show the flow topology parameter.
3.3. Bubble-bursting dynamics
In the previous section, we identified different regimes as a function of ![]() ${{\textit {De}}}$ and
${{\textit {De}}}$ and ![]() $\mathcal {J}$. Here, we analyse the transient development of the bubble-bursting process. To demystify the different stages of the bubble-bursting process, we will compare the dynamics of bubble bursting in an EVP medium with that of a Newtonian fluid. The latter is well documented in Duchemin et al. (Reference Duchemin, Popinet, Josserand and Zaleski2002), Ghabache & Séon (Reference Ghabache and Séon2016), Deike et al. (Reference Deike, Ghabache, Liger-Belair, Das, Zaleski, Popinet and Séon2018), Gordillo & Rodríguez-Rodríguez (Reference Gordillo and Rodríguez-Rodríguez2019) and Berny et al. (Reference Berny, Deike, Séon and Popinet2020). The bubble bursting in a Newtonian liquid (
$\mathcal {J}$. Here, we analyse the transient development of the bubble-bursting process. To demystify the different stages of the bubble-bursting process, we will compare the dynamics of bubble bursting in an EVP medium with that of a Newtonian fluid. The latter is well documented in Duchemin et al. (Reference Duchemin, Popinet, Josserand and Zaleski2002), Ghabache & Séon (Reference Ghabache and Séon2016), Deike et al. (Reference Deike, Ghabache, Liger-Belair, Das, Zaleski, Popinet and Séon2018), Gordillo & Rodríguez-Rodríguez (Reference Gordillo and Rodríguez-Rodríguez2019) and Berny et al. (Reference Berny, Deike, Séon and Popinet2020). The bubble bursting in a Newtonian liquid (![]() $\mathcal {J} = 0$,
$\mathcal {J} = 0$, ![]() ${{\textit {De}}} = 0$) is characterized by the retraction of the rim leading to the formation of capillary waves. The capillary waves travel towards the bottom of the bubble cavity resulting in the formation of a Worthington jet, which can then break into multiple droplets owing to the end-pinching and Rayleigh–Plateau instabilities (Walls et al. Reference Walls, Henaux and Bird2015). Furthermore, owing to the conservation of momentum, a high-velocity jet is also formed in an opposite direction to the Worthington jet, inside the liquid pool. Figure 5(a) illustrates the process of bubble bursting in a Newtonian fluid medium and identifies the state of flow inside the liquid medium using the flow topology parameter
${{\textit {De}}} = 0$) is characterized by the retraction of the rim leading to the formation of capillary waves. The capillary waves travel towards the bottom of the bubble cavity resulting in the formation of a Worthington jet, which can then break into multiple droplets owing to the end-pinching and Rayleigh–Plateau instabilities (Walls et al. Reference Walls, Henaux and Bird2015). Furthermore, owing to the conservation of momentum, a high-velocity jet is also formed in an opposite direction to the Worthington jet, inside the liquid pool. Figure 5(a) illustrates the process of bubble bursting in a Newtonian fluid medium and identifies the state of flow inside the liquid medium using the flow topology parameter ![]() $\mathcal {Q}$ defined as
$\mathcal {Q}$ defined as
where ![]() $\|\boldsymbol {\mathcal {D}}\| = \sqrt {(\boldsymbol {\mathcal {D}} \colon \boldsymbol {\mathcal {D}})/2}$ and
$\|\boldsymbol {\mathcal {D}}\| = \sqrt {(\boldsymbol {\mathcal {D}} \colon \boldsymbol {\mathcal {D}})/2}$ and ![]() $\|\boldsymbol {\mathcal {S}}\| = \sqrt {(\boldsymbol {\mathcal {S}}:\boldsymbol {\mathcal {S}})/2}$, with
$\|\boldsymbol {\mathcal {S}}\| = \sqrt {(\boldsymbol {\mathcal {S}}:\boldsymbol {\mathcal {S}})/2}$, with ![]() $\boldsymbol {\mathcal {S}}$ denoting the rate of rotation tensor defined as
$\boldsymbol {\mathcal {S}}$ denoting the rate of rotation tensor defined as ![]() $\boldsymbol {\mathcal {S}} = ((\boldsymbol {\nabla } \boldsymbol {u})^{\rm T} - \boldsymbol {\nabla } \boldsymbol {u})/2$. When
$\boldsymbol {\mathcal {S}} = ((\boldsymbol {\nabla } \boldsymbol {u})^{\rm T} - \boldsymbol {\nabla } \boldsymbol {u})/2$. When ![]() $\mathcal {Q} = -1$, the flow is purely rotational, whereas regions with
$\mathcal {Q} = -1$, the flow is purely rotational, whereas regions with ![]() $\mathcal {Q}=0$ represent pure shear flow and
$\mathcal {Q}=0$ represent pure shear flow and ![]() $\mathcal {Q} = 1$ corresponds to either elongational flow or no flow (i.e.
$\mathcal {Q} = 1$ corresponds to either elongational flow or no flow (i.e. ![]() $\|\boldsymbol {\mathcal {D}}\| \rightarrow 0, \|\boldsymbol {\mathcal {S}}\| \rightarrow 0$).
$\|\boldsymbol {\mathcal {D}}\| \rightarrow 0, \|\boldsymbol {\mathcal {S}}\| \rightarrow 0$).
Bursting bubble in an EVP fluid exhibits a non-monotonic behaviour in the jet development process, as shown in figure 5(b–d). The figure illustrates three representative cases, identifying the effects of elastic stress relaxation on the bubble bursting process in an EVP fluid (supplementary movies are available at Balasubramanian (Reference Balasubramanian2023)) for a given plastocapillary number of ![]() $\mathcal {J}=0.1$. The left-hand and right-hand subpanels of figure 5(b–d) show the flow topology parameter
$\mathcal {J}=0.1$. The left-hand and right-hand subpanels of figure 5(b–d) show the flow topology parameter ![]() $\mathcal {Q}$ and the trace of elastic stresses on a
$\mathcal {Q}$ and the trace of elastic stresses on a ![]() $\mathrm {log_{10}}$ scale, respectively. Note that the early-time dynamics (
$\mathrm {log_{10}}$ scale, respectively. Note that the early-time dynamics (![]() $t \lessapprox 0.4$) appear similar in figure 5(b–d), but exhibit qualitatively different behaviour at later times. At low
$t \lessapprox 0.4$) appear similar in figure 5(b–d), but exhibit qualitatively different behaviour at later times. At low ![]() ${{\textit {De}}}$, droplet formation is observed which is eventually suppressed by elastic stresses for intermediate values of
${{\textit {De}}}$, droplet formation is observed which is eventually suppressed by elastic stresses for intermediate values of ![]() ${{\textit {De}}}$. For large relaxation time (i.e. at higher
${{\textit {De}}}$. For large relaxation time (i.e. at higher ![]() ${{\textit {De}}}$), the elastic stresses persist and are concentrated close to the jet. The jet is characterized by larger axial stress in the elongational flow region of the jet (characterized by high shear
${{\textit {De}}}$), the elastic stresses persist and are concentrated close to the jet. The jet is characterized by larger axial stress in the elongational flow region of the jet (characterized by high shear ![]() $\mathcal {Q}\approx 0$), and extra stress opposes the capillary stress, inhibiting the droplet formation from the jet. This observation of droplet prevention due to the addition of polymers was also discussed by Rodríguez-Díaz et al. (Reference Rodríguez-Díaz, Rubio, Montanero, Gañán-Calvo and Cabezas2023) and Dixit et al. (Reference Dixit, Oratis, Zinelis, Lohse and Sanjay2024). At even higher values of
$\mathcal {Q}\approx 0$), and extra stress opposes the capillary stress, inhibiting the droplet formation from the jet. This observation of droplet prevention due to the addition of polymers was also discussed by Rodríguez-Díaz et al. (Reference Rodríguez-Díaz, Rubio, Montanero, Gañán-Calvo and Cabezas2023) and Dixit et al. (Reference Dixit, Oratis, Zinelis, Lohse and Sanjay2024). At even higher values of ![]() ${{\textit {De}}}$ (i.e.
${{\textit {De}}}$ (i.e. ![]() ${{\textit {De}}}=20$), we observe again a persistent Worthington jet that thins appreciatively over time (see figure 5c). Due to low elastocapillary number, the bulk medium remains unyielded and behaves as a Kelvin–Voigt viscoelastic solid with negligible
${{\textit {De}}}=20$), we observe again a persistent Worthington jet that thins appreciatively over time (see figure 5c). Due to low elastocapillary number, the bulk medium remains unyielded and behaves as a Kelvin–Voigt viscoelastic solid with negligible ![]() $\mathrm {tr}(\boldsymbol {\tau _p})$. In contrast, the axial region of the jet experiences significant extra stress, and as the jet continues to thin, it eventually pinches off when its thickness becomes smaller than the grid size.
$\mathrm {tr}(\boldsymbol {\tau _p})$. In contrast, the axial region of the jet experiences significant extra stress, and as the jet continues to thin, it eventually pinches off when its thickness becomes smaller than the grid size.
It is essential to note that the appearance of the yielded region (![]() $K \neq 0$) is influenced not only by the plasticity of the fluid but also by the elastic stress (
$K \neq 0$) is influenced not only by the plasticity of the fluid but also by the elastic stress (![]() $\tau _p$), which affects the yield criterion (refer to (2.8)). For
$\tau _p$), which affects the yield criterion (refer to (2.8)). For ![]() $\mathcal {J}=0.1$, at low
$\mathcal {J}=0.1$, at low ![]() ${{\textit {De}}}$, we observe a large yielded region exhibiting significant elastic deformation from the base state (i.e.
${{\textit {De}}}$, we observe a large yielded region exhibiting significant elastic deformation from the base state (i.e. ![]() $A \neq I$). Hence, the resulting elastic stresses relax more rapidly due to shorter relaxation times. This fast extra stress relaxation, especially at low
$A \neq I$). Hence, the resulting elastic stresses relax more rapidly due to shorter relaxation times. This fast extra stress relaxation, especially at low ![]() ${{\textit {De}}}$, causes the EVP medium to behave similarly to a Newtonian fluid, as evidenced by the similar busting bubble dynamics. However, it is worth noting that the resulting jet formation differs from the Newtonian case at
${{\textit {De}}}$, causes the EVP medium to behave similarly to a Newtonian fluid, as evidenced by the similar busting bubble dynamics. However, it is worth noting that the resulting jet formation differs from the Newtonian case at ![]() ${{\textit {Oh}}}=10^{-2}$ as the introduction of yield stress increases the apparent viscosity (see § 3.1) of the fluid and alters the flow. Note that the maximum magnitude of elastic deformation occurs mainly in the region of high shear around the time when capillary waves converge at the bottom of the bubble cavity, resulting in jet formation. With increasing
${{\textit {Oh}}}=10^{-2}$ as the introduction of yield stress increases the apparent viscosity (see § 3.1) of the fluid and alters the flow. Note that the maximum magnitude of elastic deformation occurs mainly in the region of high shear around the time when capillary waves converge at the bottom of the bubble cavity, resulting in jet formation. With increasing ![]() ${{\textit {De}}}$ at fixed
${{\textit {De}}}$ at fixed ![]() ${{\textit {Oh}}}_p$, the elastocapillary number decreases, indicating lower elastic energy in the EVP fluid (refer to § 3.7) and thereby, the yielded region appears in the proximity of the jet. The elastic stresses are lower in the majority of the bulk, which remains unyielded (
${{\textit {Oh}}}_p$, the elastocapillary number decreases, indicating lower elastic energy in the EVP fluid (refer to § 3.7) and thereby, the yielded region appears in the proximity of the jet. The elastic stresses are lower in the majority of the bulk, which remains unyielded (![]() $K = 0$) and exhibits a Kelvin–Voigt viscoelastic solid behaviour (
$K = 0$) and exhibits a Kelvin–Voigt viscoelastic solid behaviour (![]() $\boldsymbol {\overset {\nabla }{A}} = \boldsymbol {0}$). (Note that the higher elastic stresses can be found in the yielded region of the EVP fluid where
$\boldsymbol {\overset {\nabla }{A}} = \boldsymbol {0}$). (Note that the higher elastic stresses can be found in the yielded region of the EVP fluid where ![]() $\mathrm {tr}(\boldsymbol {A})$ can be larger.) At high
$\mathrm {tr}(\boldsymbol {A})$ can be larger.) At high ![]() ${{\textit {De}}}$, a significant portion of the EVP fluid behaves as an elastic solid with very low elastic modulus, which allows the development of a high and thin jet, leading to capillary-type instability and pearl or drop formation. At
${{\textit {De}}}$, a significant portion of the EVP fluid behaves as an elastic solid with very low elastic modulus, which allows the development of a high and thin jet, leading to capillary-type instability and pearl or drop formation. At ![]() ${{\textit {De}}} = 20$ (refer to figure 5c), we observe jet formation reminiscent of the bead-on-a-string instability, which has been suggested to be the elastic counterpart of the Rayleigh–Plateau instability, and is observed in both viscoelastic fluids and elastic solids (Kibbelaar et al. Reference Kibbelaar, Deblais, Burla, Koenderink, Velikov and Bonn2020).
${{\textit {De}}} = 20$ (refer to figure 5c), we observe jet formation reminiscent of the bead-on-a-string instability, which has been suggested to be the elastic counterpart of the Rayleigh–Plateau instability, and is observed in both viscoelastic fluids and elastic solids (Kibbelaar et al. Reference Kibbelaar, Deblais, Burla, Koenderink, Velikov and Bonn2020).
The effects of increasing plasticity (via plastocapillary number ![]() $\mathcal {J}$) are shown in figure 6, at a small Deborah number (
$\mathcal {J}$) are shown in figure 6, at a small Deborah number (![]() ${{\textit {De}}}=0.04$). We observe that with the addition of plasticity, jet formation is monotonically suppressed. This is due to the increased apparent viscosity, as discussed in § 3.1.
${{\textit {De}}}=0.04$). We observe that with the addition of plasticity, jet formation is monotonically suppressed. This is due to the increased apparent viscosity, as discussed in § 3.1.

Figure 6. Variation of the dynamics of bubble bursting in an EVP medium with respect to ![]() $\mathcal {J}$ at
$\mathcal {J}$ at ![]() ${{\textit {De}}}=0.04$: (a)
${{\textit {De}}}=0.04$: (a) ![]() $\mathcal {J}=0.01$; (b)
$\mathcal {J}=0.01$; (b) ![]() $\mathcal {J}=0.1$; (c)
$\mathcal {J}=0.1$; (c) ![]() $\mathcal {J}=0.8$. The left-hand part of each subpanel shows the flow topology parameter
$\mathcal {J}=0.8$. The left-hand part of each subpanel shows the flow topology parameter ![]() $\mathcal {Q}$ and the right-hand part of the subpanel shows the trace of elastic stress on a
$\mathcal {Q}$ and the right-hand part of the subpanel shows the trace of elastic stress on a ![]() $\log _{10}$ scale. The yielded regions are marked by a grey line, which corresponds to
$\log _{10}$ scale. The yielded regions are marked by a grey line, which corresponds to ![]() $\mathcal {J}\approxeq \|\boldsymbol {\tau _d}\|$.
$\mathcal {J}\approxeq \|\boldsymbol {\tau _d}\|$.
For a lower ![]() ${{\textit {De}}}$, the elastic stresses relax quickly, and the material behaves as a viscous fluid when the elastic stresses are negligible. Here, for the considered
${{\textit {De}}}$, the elastic stresses relax quickly, and the material behaves as a viscous fluid when the elastic stresses are negligible. Here, for the considered ![]() ${{\textit {De}}}\sim O(0.01)$, the elastocapillary number is higher, indicating that most of the EVP fluid region is yielded and the magnitude of elastic energy is high as observed from figure 6(a–c). Then, for a lower
${{\textit {De}}}\sim O(0.01)$, the elastocapillary number is higher, indicating that most of the EVP fluid region is yielded and the magnitude of elastic energy is high as observed from figure 6(a–c). Then, for a lower ![]() $\mathcal {J}$,
$\mathcal {J}$, ![]() $K \neq 0$ over a significant portion of the EVP fluid, indicating a larger yielded region around the axis of cavity and jet. With an increase in the plasticity of the EVP fluid, the yielded region decreases for a given
$K \neq 0$ over a significant portion of the EVP fluid, indicating a larger yielded region around the axis of cavity and jet. With an increase in the plasticity of the EVP fluid, the yielded region decreases for a given ![]() ${{\textit {De}}}$. However, as mentioned earlier, it is essential to note that the elastic stress also plays a role in influencing the yield criterion
${{\textit {De}}}$. However, as mentioned earlier, it is essential to note that the elastic stress also plays a role in influencing the yield criterion ![]() $K$.
$K$.
Finally, we examine the combination of moderate to considerable plasticity (![]() $\mathcal {J}=1$) and different relaxation time of elastic stresses (see figure 7). The behaviour is qualitatively similar to that observed at
$\mathcal {J}=1$) and different relaxation time of elastic stresses (see figure 7). The behaviour is qualitatively similar to that observed at ![]() $\mathcal {J} = 0.1$. However, at low
$\mathcal {J} = 0.1$. However, at low ![]() ${{\textit {De}}}$ (figure 7a), jet formation is wholly suppressed, indicating that the EVP fluid takes on the characteristics of a viscoplastic fluid. The deformation of the bubble cavity is significantly dampened by both the yielded region (with increased apparent viscosity) and the unyielded region (with high elastic modulus because of high
${{\textit {De}}}$ (figure 7a), jet formation is wholly suppressed, indicating that the EVP fluid takes on the characteristics of a viscoplastic fluid. The deformation of the bubble cavity is significantly dampened by both the yielded region (with increased apparent viscosity) and the unyielded region (with high elastic modulus because of high ![]() $Ec$). For
$Ec$). For ![]() ${{\textit {De}}}\ge 1$, the jet is pronounced due to lower elastic energy than capillary energy (low elastocapillary numbers). Further, for
${{\textit {De}}}\ge 1$, the jet is pronounced due to lower elastic energy than capillary energy (low elastocapillary numbers). Further, for ![]() ${{\textit {De}}}=20$ at
${{\textit {De}}}=20$ at ![]() $t=0.95$ the growth of elastic instability compensated by the surface tension forces in the jet hints at the appearance of bead-in-a-string characteristic. At medium
$t=0.95$ the growth of elastic instability compensated by the surface tension forces in the jet hints at the appearance of bead-in-a-string characteristic. At medium ![]() ${{\textit {De}}}$, however, the elastic stresses and plasticity acts together to broaden and suppress the jet formation. In the forthcoming subsections, we will scrutinize the effect of EVP rheology on each stage of the bubble-bursting process.
${{\textit {De}}}$, however, the elastic stresses and plasticity acts together to broaden and suppress the jet formation. In the forthcoming subsections, we will scrutinize the effect of EVP rheology on each stage of the bubble-bursting process.

Figure 7. Variation of the dynamics of bubble bursting in an EVP medium with respect to ![]() ${{\textit {De}}}$ at
${{\textit {De}}}$ at ![]() $\mathcal {J}=1$: (a)
$\mathcal {J}=1$: (a) ![]() ${{\textit {De}}}=0.01$; (b)
${{\textit {De}}}=0.01$; (b) ![]() ${{\textit {De}}}=16$; (c)
${{\textit {De}}}=16$; (c) ![]() ${{\textit {De}}}=20$. The left-hand part of each subpanel shows the flow topology parameter
${{\textit {De}}}=20$. The left-hand part of each subpanel shows the flow topology parameter ![]() $\mathcal {Q}$ and the right-hand part of the subpanel shows the trace of elastic stress on a
$\mathcal {Q}$ and the right-hand part of the subpanel shows the trace of elastic stress on a ![]() $\log _{10}$ scale. The yielded regions are marked by a grey line, which corresponds to
$\log _{10}$ scale. The yielded regions are marked by a grey line, which corresponds to ![]() $\mathcal {J}\approxeq \|\boldsymbol {\tau _d}\|$.
$\mathcal {J}\approxeq \|\boldsymbol {\tau _d}\|$.
3.4. Capillary waves in the presence of yield stress and elastic stress
Capillary waves are critical in the bubble-bursting process (Gordillo & Rodríguez-Rodríguez Reference Gordillo and Rodríguez-Rodríguez2019; Sanjay et al. Reference Sanjay, Lohse and Jalaal2021). Initially, as the film breaks and the rim retracts, they create a series of capillary waves with varying strengths (Gekle et al. Reference Gekle, Gordillo, van der Meer and Lohse2009). However, the high-frequency capillary waves experience substantial viscous damping. Consequently, the process of wave focusing and jet formation is controlled by the strongest wave, which remains unimpeded by viscous damping. Here, we track the strongest wave by monitoring the maximum curvature of the free-surface wave ![]() $(\|\kappa _c\|$, see inset of figure 8a for the location (
$(\|\kappa _c\|$, see inset of figure 8a for the location (![]() $\theta _c$) of the strongest capillary wave), as in Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021), to understand the combined role of elastic stress relaxation and plasticity in jet formation.
$\theta _c$) of the strongest capillary wave), as in Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021), to understand the combined role of elastic stress relaxation and plasticity in jet formation.

Figure 8. Effects of dimensionless relaxation time on the travelling capillary waves at ![]() $\mathcal {J}=1$. (a) Time variation of the location of strongest capillary wave
$\mathcal {J}=1$. (a) Time variation of the location of strongest capillary wave ![]() $(\theta _c)$ for different
$(\theta _c)$ for different ![]() ${{\textit {De}}}$. (b) Corresponding time variation of the strength of strongest capillary wave
${{\textit {De}}}$. (b) Corresponding time variation of the strength of strongest capillary wave ![]() $(\|\kappa _c\|)$.
$(\|\kappa _c\|)$.
The location and amplitude of the strongest capillary wave as a function of the Deborah number are shown in figure 8 (for ![]() $\mathcal {J}=1$). In the case of Newtonian fluid, the capillary wave travels with a constant inertiocapillary velocity
$\mathcal {J}=1$). In the case of Newtonian fluid, the capillary wave travels with a constant inertiocapillary velocity ![]() $(\sim V_\gamma )$ as shown in figure 8(a) (dashed line). However, the viscous stress impedes these waves, resulting in the decrease of the strength of the wave (
$(\sim V_\gamma )$ as shown in figure 8(a) (dashed line). However, the viscous stress impedes these waves, resulting in the decrease of the strength of the wave (![]() $\|\kappa _c\|)$, as observed in figure 8(b). For
$\|\kappa _c\|)$, as observed in figure 8(b). For ![]() $\theta _c/{\rm \pi} \approx 0.5$, the cavity geometry changes, leading to flow focusing where an increase in strength of the capillary wave is observed.
$\theta _c/{\rm \pi} \approx 0.5$, the cavity geometry changes, leading to flow focusing where an increase in strength of the capillary wave is observed.
From figure 8, we observe that the location of the strongest wave is not significantly affected by elastic stresses in the EVP fluid. Consequently, the strongest elastocapillary waves still travel with the inertiocapillary velocity ![]() $V_\gamma$, due to the high shear yielded region close to the cavity interface, which behaves as a viscoelastic fluid. However, at low
$V_\gamma$, due to the high shear yielded region close to the cavity interface, which behaves as a viscoelastic fluid. However, at low ![]() ${{\textit {De}}}$, as the material approaches the viscoplastic limit, the location of the strongest wave tends to deviate from that of the Newtonian fluid, particularly in the flow-focusing part around
${{\textit {De}}}$, as the material approaches the viscoplastic limit, the location of the strongest wave tends to deviate from that of the Newtonian fluid, particularly in the flow-focusing part around ![]() $t\approx 0.3$ owing to enhanced apparent viscosity. At low
$t\approx 0.3$ owing to enhanced apparent viscosity. At low ![]() ${{\textit {De}}}$, the strength of the capillary wave is also notably reduced, as evident in figure 8(b), due to both viscous and polymer dissipation (see also § 3.7). The combined dissipation mitigates the jet formation. The increased polymeric dissipation is due to the faster relaxation of the elastic stresses close to the free surface where the fluid is yielded. Conversely, for high
${{\textit {De}}}$, the strength of the capillary wave is also notably reduced, as evident in figure 8(b), due to both viscous and polymer dissipation (see also § 3.7). The combined dissipation mitigates the jet formation. The increased polymeric dissipation is due to the faster relaxation of the elastic stresses close to the free surface where the fluid is yielded. Conversely, for high ![]() ${{\textit {De}}}$, the elastocapillary number decreases, and the corresponding deformation of the cavity results in the presence of a stronger capillary wave than in the Newtonian case.
${{\textit {De}}}$, the elastocapillary number decreases, and the corresponding deformation of the cavity results in the presence of a stronger capillary wave than in the Newtonian case.
We now investigate the role of plasticity in the propagation of capillary waves at low ![]() ${{\textit {De}}}$. In figure 9(a), we observe that the elastocapillary waves travel with the same inertiocapillary velocity
${{\textit {De}}}$. In figure 9(a), we observe that the elastocapillary waves travel with the same inertiocapillary velocity ![]() $V_\gamma$ and show no deviation from the Newtonian case for the range of considered plastocapillary numbers in this study. At low
$V_\gamma$ and show no deviation from the Newtonian case for the range of considered plastocapillary numbers in this study. At low ![]() ${{\textit {De}}}$,
${{\textit {De}}}$, ![]() $\mathcal {J}$ primarily influences the yield-criterion (
$\mathcal {J}$ primarily influences the yield-criterion (![]() $K$). For the
$K$). For the ![]() $\mathcal {J}$ range in this study, the region close to the cavity interface is yielded and behaves as a viscoelastic fluid. Consequently, the propagation of capillary waves is unaffected by an increase in
$\mathcal {J}$ range in this study, the region close to the cavity interface is yielded and behaves as a viscoelastic fluid. Consequently, the propagation of capillary waves is unaffected by an increase in ![]() $\mathcal {J}$. However, an increase in
$\mathcal {J}$. However, an increase in ![]() $\mathcal {J}$ increases the apparent viscosity leading to attenuation of the strongest capillary wave and mitigation of the Worthington jet, following the mechanism proposed by Gordillo & Rodríguez-Rodríguez (Reference Gordillo and Rodríguez-Rodríguez2019) and Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021) for Newtonian and purely Bingham fluids, respectively (figures 9b and 6).
$\mathcal {J}$ increases the apparent viscosity leading to attenuation of the strongest capillary wave and mitigation of the Worthington jet, following the mechanism proposed by Gordillo & Rodríguez-Rodríguez (Reference Gordillo and Rodríguez-Rodríguez2019) and Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021) for Newtonian and purely Bingham fluids, respectively (figures 9b and 6).

Figure 9. Effects of plasticity on the travelling capillary waves at ![]() ${{\textit {De}}}=0.01$. (a) Time variation of the location of strongest capillary wave
${{\textit {De}}}=0.01$. (a) Time variation of the location of strongest capillary wave ![]() $(\theta _c)$ for different
$(\theta _c)$ for different ![]() $\mathcal {J}$. (b) Corresponding time variation of the strength of strongest capillary wave
$\mathcal {J}$. (b) Corresponding time variation of the strength of strongest capillary wave ![]() $(\|\kappa _c\|)$.
$(\|\kappa _c\|)$.
The EVP fluid studied here features a notable distinction from the purely Bingham fluids. Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021) noted that the damping of capillary waves leads to the retention of surface energy, culminating in non-flat final shapes. This phenomenon contrasts with the behaviour of EVP fluids. In EVP fluids, the high elastic modulus imparts solid-like characteristics, particularly in the context of elastic stress relaxation. During the cavity deformation process, these stresses accumulate and only dissipate gradually. This slow relaxation is responsible for the eventual deformation of the cavity over time depending on elastocapillary number, a stark difference from the Bingham fluid case where such deformation is impeded by the stored surface energy.
3.5. Influence of elastic stress relaxation time and yield stress on jet formation
One of the key characteristics of the bubble-bursting process is the formation of the Worthington jet (![]() $-\mathcal {H}>0$ at
$-\mathcal {H}>0$ at ![]() $\mathcal {R} = 0$) following the collapse of the bubble cavity. Figure 10 illustrates the temporal evolution of the jet for different
$\mathcal {R} = 0$) following the collapse of the bubble cavity. Figure 10 illustrates the temporal evolution of the jet for different ![]() ${{\textit {De}}}$. From figure 10(a), an increase in
${{\textit {De}}}$. From figure 10(a), an increase in ![]() ${{\textit {De}}}$ of the EVP fluid pronounces the jet growth and the maximum height of the jet. For
${{\textit {De}}}$ of the EVP fluid pronounces the jet growth and the maximum height of the jet. For ![]() ${{\textit {De}}} \sim O(1)$, the elastic stresses in the jet do not relax and compensate the capillary stresses resulting in the prevention of droplet breakup from the jet.
${{\textit {De}}} \sim O(1)$, the elastic stresses in the jet do not relax and compensate the capillary stresses resulting in the prevention of droplet breakup from the jet.

Figure 10. Effects of non-dimensional elastic stress relaxation time on the formation of jet as a result of the collapsing cavity. Variation of the depth ![]() $\mathcal {H}$ of the cavity at its axis with time for (a) high Deborah numbers and (b) for low Deborah numbers at
$\mathcal {H}$ of the cavity at its axis with time for (a) high Deborah numbers and (b) for low Deborah numbers at ![]() $\mathcal {J}=0.1$. The inset in (a) shows the definition of
$\mathcal {J}=0.1$. The inset in (a) shows the definition of ![]() $\mathcal {H}$ and the inset in (b) depicts the pinch-off process.
$\mathcal {H}$ and the inset in (b) depicts the pinch-off process.
However, from figure 10(b), for ![]() ${{\textit {De}}} \le 0.04$, we observe the droplet formation as the elastic stresses (also relaxing faster) are overcome by the capillary forces. However, it is intuitive to note that as Deborah number increases for
${{\textit {De}}} \le 0.04$, we observe the droplet formation as the elastic stresses (also relaxing faster) are overcome by the capillary forces. However, it is intuitive to note that as Deborah number increases for ![]() ${{\textit {De}}}\sim O(0.01)$, the maximum jet height decreases. The same behaviour is also observed at
${{\textit {De}}}\sim O(0.01)$, the maximum jet height decreases. The same behaviour is also observed at ![]() $\mathcal {J}=1$ (not shown here due to brevity) where the droplet pinch-off is not observed. The decrease in jet development at low but increasing
$\mathcal {J}=1$ (not shown here due to brevity) where the droplet pinch-off is not observed. The decrease in jet development at low but increasing ![]() ${{\textit {De}}}$ (as shown in figure 10b) is due to relatively slower relaxation of elastic stresses and thereby increased storage of elastic energy at the time when capillary waves collapse at the bottom of the cavity, i.e. during jet initiation (refer to Appendix F). Apart from this, combined effects of increasing viscous dissipation and decreasing polymeric dissipation also contributes to the behaviour of jet development. However, as
${{\textit {De}}}$ (as shown in figure 10b) is due to relatively slower relaxation of elastic stresses and thereby increased storage of elastic energy at the time when capillary waves collapse at the bottom of the cavity, i.e. during jet initiation (refer to Appendix F). Apart from this, combined effects of increasing viscous dissipation and decreasing polymeric dissipation also contributes to the behaviour of jet development. However, as ![]() ${{\textit {De}}}$ increases (for
${{\textit {De}}}$ increases (for ![]() ${{\textit {De}}}\sim O(1)$ as highlighted in figure 10a), the elastocapillary number decreases indicating lower elastic energy, which pronounces the jet height (refer to Appendix F).
${{\textit {De}}}\sim O(1)$ as highlighted in figure 10a), the elastocapillary number decreases indicating lower elastic energy, which pronounces the jet height (refer to Appendix F).
Figure 11 reveals that for ![]() ${{\textit {De}}}\sim O(1)$ (i.e. in the viscoelastocapillary regime), plasticity does not appear to have a significant impact on jet development. However, as the relaxation time of the elastic stress decreases in the EVP fluid, the influence of plasticity becomes more pronounced, resulting in the reduction of jet growth.
${{\textit {De}}}\sim O(1)$ (i.e. in the viscoelastocapillary regime), plasticity does not appear to have a significant impact on jet development. However, as the relaxation time of the elastic stress decreases in the EVP fluid, the influence of plasticity becomes more pronounced, resulting in the reduction of jet growth.

Figure 11. Effects of plasticity on the formation of jet as a result of the collapsing cavity. Variation of the depth ![]() $\mathcal {H}$ of the cavity at its axis with time at (a)
$\mathcal {H}$ of the cavity at its axis with time at (a) ![]() ${{\textit {De}}}=2$ and (b)
${{\textit {De}}}=2$ and (b) ![]() ${{\textit {De}}}=0.02$.
${{\textit {De}}}=0.02$.
Figure 12 illustrates the variation in the maximum jet height ![]() $(-\mathcal {H}_{max})$ with respect to dimensionless relaxation time of the elastic stresses in the EVP fluid. In the viscoelastocapillary regime, the trend with which the maximum height of the jet varies is logarithmic with respect to
$(-\mathcal {H}_{max})$ with respect to dimensionless relaxation time of the elastic stresses in the EVP fluid. In the viscoelastocapillary regime, the trend with which the maximum height of the jet varies is logarithmic with respect to ![]() ${{\textit {De}}}$.
${{\textit {De}}}$.

Figure 12. Effects of elastic stress relaxation on the maximum height of Worthington jet formation. The darker markers correspond to higher ![]() $\mathcal {J}$ and vice versa.
$\mathcal {J}$ and vice versa.
In figure 13, we present the variation of jet velocity in relation to ![]() ${{\textit {De}}}$. In this context, the jet velocity is defined as the vertical velocity of the interface at the axis. We use
${{\textit {De}}}$. In this context, the jet velocity is defined as the vertical velocity of the interface at the axis. We use ![]() $v_e$ to represent the velocity of the jet as it crosses the free-flat equilibrium surface, specifically
$v_e$ to represent the velocity of the jet as it crosses the free-flat equilibrium surface, specifically ![]() $v_e = v(\mathcal {Z}=\mathcal {R}=0)$. Note that Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014) have utilized a similar quantification of jet velocity in the experiments of bubble bursting in a Newtonian medium. Additionally, we also sample
$v_e = v(\mathcal {Z}=\mathcal {R}=0)$. Note that Ghabache et al. (Reference Ghabache, Antkowiak, Josserand and Séon2014) have utilized a similar quantification of jet velocity in the experiments of bubble bursting in a Newtonian medium. Additionally, we also sample ![]() $v_{max}$, which corresponds to the maximum vertical velocity of the interface along the axis (Gordillo & Rodríguez-Rodríguez Reference Gordillo and Rodríguez-Rodríguez2019; Sanjay et al. Reference Sanjay, Lohse and Jalaal2021; Gordillo & Blanco-Rodríguez Reference Gordillo and Blanco-Rodríguez2023). Typically, this maximum velocity occurs when capillary waves merge at the bottom of the bubble cavity. We hypothesize that the maximum interface velocity
$v_{max}$, which corresponds to the maximum vertical velocity of the interface along the axis (Gordillo & Rodríguez-Rodríguez Reference Gordillo and Rodríguez-Rodríguez2019; Sanjay et al. Reference Sanjay, Lohse and Jalaal2021; Gordillo & Blanco-Rodríguez Reference Gordillo and Blanco-Rodríguez2023). Typically, this maximum velocity occurs when capillary waves merge at the bottom of the bubble cavity. We hypothesize that the maximum interface velocity ![]() $v_{max}$ at the axis represents the initiation velocity of the jet. This initiation velocity results from the conversion of capillary surface energy (due to merging capillary waves) into the kinetic energy of the jet.
$v_{max}$ at the axis represents the initiation velocity of the jet. This initiation velocity results from the conversion of capillary surface energy (due to merging capillary waves) into the kinetic energy of the jet.

Figure 13. Variation of the Worthington jet velocity with dimensionless elastic stress relaxation time. (a) Velocity of the jet at the instant when the interface crosses the equilibrium surface ![]() $(v_e)$ is plotted against
$(v_e)$ is plotted against ![]() ${{\textit {De}}}$. (b) The effects of elastic stress relaxation on the maximum velocity
${{\textit {De}}}$. (b) The effects of elastic stress relaxation on the maximum velocity ![]() $(v_{max})$ of the jet. The darker markers correspond to higher
$(v_{max})$ of the jet. The darker markers correspond to higher ![]() $\mathcal {J}$ and vice versa.
$\mathcal {J}$ and vice versa.
From figure 13(a), we observe the jet velocity at the equilibrium surface almost exhibits a logarithmic increase with ![]() ${{\textit {De}}}$. Furthermore, from figure 13(b), we notice that the initiation velocity of the jet remains relatively constant with
${{\textit {De}}}$. Furthermore, from figure 13(b), we notice that the initiation velocity of the jet remains relatively constant with ![]() ${{\textit {De}}}$ within the viscoelastocapillary regime. Consequently, the maximum kinetic energy, which arises from the energy balance at the moment of capillary wave merging at the bottom of the cavity, is minimally affected due to a decrease in the elastocapillary number in the viscoelastocapillary regime.
${{\textit {De}}}$ within the viscoelastocapillary regime. Consequently, the maximum kinetic energy, which arises from the energy balance at the moment of capillary wave merging at the bottom of the cavity, is minimally affected due to a decrease in the elastocapillary number in the viscoelastocapillary regime.
Jet formation can lead to droplet formation at low and high Deborah numbers. In this study, we qualitatively discuss the impact of elastic stress relaxation time on the droplet-formation time (![]() $t_d$) in the jet using figure 14. However, a quantitative analysis of droplet formation time is not accurate in this study due to the numerical artefact, which is detailed in Appendix C. In the near-Newtonian limit characterized by a lower relaxation time, we observe that the droplet formation time is delayed logarithmically with increasing
$t_d$) in the jet using figure 14. However, a quantitative analysis of droplet formation time is not accurate in this study due to the numerical artefact, which is detailed in Appendix C. In the near-Newtonian limit characterized by a lower relaxation time, we observe that the droplet formation time is delayed logarithmically with increasing ![]() ${{\textit {De}}}$. This delayed droplet-formation is attributed to a finite non-zero relaxation time of elastic stresses, which increases with
${{\textit {De}}}$. This delayed droplet-formation is attributed to a finite non-zero relaxation time of elastic stresses, which increases with ![]() ${{\textit {De}}}$ and thereby delays the time at which the capillary stresses overtake the elastic stresses in the jet.
${{\textit {De}}}$ and thereby delays the time at which the capillary stresses overtake the elastic stresses in the jet.

Figure 14. Variation of the droplet-formation time with respect to dimensionless relaxation time of elastic stress.
3.6. Effects of solvent–polymer viscosity ratio on Worthington jet
In figure 15 we show the effects of varying the solvent–polymer viscosity ratio in terms of ![]() $\beta \,(={{\textit {Oh}}}_s/({{\textit {Oh}}}_s+{{\textit {Oh}}}_p))$ on the jet development at different
$\beta \,(={{\textit {Oh}}}_s/({{\textit {Oh}}}_s+{{\textit {Oh}}}_p))$ on the jet development at different ![]() ${{\textit {De}}}$ in the viscoelastocapillary regime (figure 15a) and at lower
${{\textit {De}}}$ in the viscoelastocapillary regime (figure 15a) and at lower ![]() ${{\textit {De}}}$ (figure 15b). Overall, we observe that the jet development is pronounced in the viscoelastocapillary regime at
${{\textit {De}}}$ (figure 15b). Overall, we observe that the jet development is pronounced in the viscoelastocapillary regime at ![]() ${{\textit {Oh}}}_s=0.009,{{\textit {Oh}}}_p = 0.001$ (
${{\textit {Oh}}}_s=0.009,{{\textit {Oh}}}_p = 0.001$ (![]() $\beta = 0.9$) in comparison with
$\beta = 0.9$) in comparison with ![]() ${{\textit {Oh}}}_s=0.0011,\,{{\textit {Oh}}}_p = 0.0088$ (
${{\textit {Oh}}}_s=0.0011,\,{{\textit {Oh}}}_p = 0.0088$ (![]() $\beta = 0.11$). Previously, we observed that relatively decreasing polymeric dissipation in the jet accentuates the growth of the jet in the viscoelastocapillary regime (refer also to Appendix F). Additionally, increasing
$\beta = 0.11$). Previously, we observed that relatively decreasing polymeric dissipation in the jet accentuates the growth of the jet in the viscoelastocapillary regime (refer also to Appendix F). Additionally, increasing ![]() ${{\textit {Oh}}}_p$ (
${{\textit {Oh}}}_p$ (![]() $\beta \rightarrow 0$) increases the elastocapillary number, which indicates a higher elastic stress in the jet, which on relaxation dissipates energy and thereby reduces the kinetic energy of the jet.
$\beta \rightarrow 0$) increases the elastocapillary number, which indicates a higher elastic stress in the jet, which on relaxation dissipates energy and thereby reduces the kinetic energy of the jet.

Figure 15. Effects of solvent–polymer viscosity ratio on jet evolution. Variation of the depth ![]() $\mathcal {H}$ of the cavity at its axis with respect to time for (a)
$\mathcal {H}$ of the cavity at its axis with respect to time for (a) ![]() $\mathcal {J}=1$ and (b)
$\mathcal {J}=1$ and (b) ![]() $\mathcal {J}=0.01$.
$\mathcal {J}=0.01$.
We also observe a similar trend of pronounced jet development in the near-Newtonian limit, characterized by low ![]() ${{\textit {De}}}$ and
${{\textit {De}}}$ and ![]() $\mathcal {J}$, as shown in figure 16. It is important to note that a similar trend of decreasing jet growth with increasing
$\mathcal {J}$, as shown in figure 16. It is important to note that a similar trend of decreasing jet growth with increasing ![]() ${{\textit {Oh}}}_p$ was also observed for lower
${{\textit {Oh}}}_p$ was also observed for lower ![]() ${{\textit {De}}}$ at higher
${{\textit {De}}}$ at higher ![]() $\mathcal {J}$, although it is not presented here. In summary, we find that increasing
$\mathcal {J}$, although it is not presented here. In summary, we find that increasing ![]() ${{\textit {Oh}}}_p$ relative to
${{\textit {Oh}}}_p$ relative to ![]() ${{\textit {Oh}}}$ (where
${{\textit {Oh}}}$ (where ![]() ${{\textit {Oh}}} = {{\textit {Oh}}}_s + {{\textit {Oh}}}_p$) has a similar effect to an increased apparent extensional viscosity in jet development. Additionally, when
${{\textit {Oh}}} = {{\textit {Oh}}}_s + {{\textit {Oh}}}_p$) has a similar effect to an increased apparent extensional viscosity in jet development. Additionally, when ![]() $\beta$ decreases, the EVP fluid exhibits significant extensional viscosity, resulting in a thicker jet as evident in figure 16.
$\beta$ decreases, the EVP fluid exhibits significant extensional viscosity, resulting in a thicker jet as evident in figure 16.

Figure 16. Variation of jet thickness with respect to solvent–polymer viscosity ratio quantified by ![]() $\beta \, (={{\textit {Oh}}}_s/({{\textit {Oh}}}_s+{{\textit {Oh}}}_p))$ at (a)
$\beta \, (={{\textit {Oh}}}_s/({{\textit {Oh}}}_s+{{\textit {Oh}}}_p))$ at (a) ![]() $t=0.6$, (b)
$t=0.6$, (b) ![]() $t=0.7$ for
$t=0.7$ for ![]() $\mathcal {J}=0.01$ and
$\mathcal {J}=0.01$ and ![]() ${{\textit {De}}}=0.08$.
${{\textit {De}}}=0.08$.
With the above results, we probe into the modification of the regime map as plotted in figure 4 with respect to ![]() $\beta$. In figure 15(b), note that we are in the droplet formation regime when
$\beta$. In figure 15(b), note that we are in the droplet formation regime when ![]() ${{\textit {De}}} = 0.01$. At this specific parameter point (
${{\textit {De}}} = 0.01$. At this specific parameter point (![]() ${{\textit {De}}}$,
${{\textit {De}}}$, ![]() $\mathcal {J}$), different
$\mathcal {J}$), different ![]() $(\beta )$ exhibit droplet formation behaviour. However, when we increase
$(\beta )$ exhibit droplet formation behaviour. However, when we increase ![]() ${{\textit {De}}}$ from
${{\textit {De}}}$ from ![]() $0.01$ to
$0.01$ to ![]() $0.08$ (crossing the green boundary along
$0.08$ (crossing the green boundary along ![]() ${{\textit {De}}}$ from the droplet formation regime to the no-pinch-off regime in figure 4), we observe that droplet formation is hindered for
${{\textit {De}}}$ from the droplet formation regime to the no-pinch-off regime in figure 4), we observe that droplet formation is hindered for ![]() $\beta = 0.5$. It is important to note that in figure 15(b), droplet formation is indicated by the discontinuity in
$\beta = 0.5$. It is important to note that in figure 15(b), droplet formation is indicated by the discontinuity in ![]() $\mathcal {H}$ (refer to the inset in figure 10b). For
$\mathcal {H}$ (refer to the inset in figure 10b). For ![]() $\beta =0.9$, however, droplet formation persists at a higher
$\beta =0.9$, however, droplet formation persists at a higher ![]() ${{\textit {De}}}$, suggesting that the (green) boundary separating the droplet formation and no-pinch-off regimes shifts upwards to accommodate a higher
${{\textit {De}}}$, suggesting that the (green) boundary separating the droplet formation and no-pinch-off regimes shifts upwards to accommodate a higher ![]() ${{\textit {De}}}$ in the case of higher
${{\textit {De}}}$ in the case of higher ![]() ${{\textit {Oh}}}_s$. Conversely, as
${{\textit {Oh}}}_s$. Conversely, as ![]() ${{\textit {Oh}}}_p$ increases, the boundary would move closer to a lower
${{\textit {Oh}}}_p$ increases, the boundary would move closer to a lower ![]() ${{\textit {De}}}$.
${{\textit {De}}}$.
Considering figure 15(a), we can examine the transition boundary between the no-jet and no-pinch-off regimes (orange boundary along ![]() ${{\textit {De}}}$ in figure 4). For
${{\textit {De}}}$ in figure 4). For ![]() ${{\textit {De}}}=1$, we observe that the maximum jet height decreases with increasing
${{\textit {De}}}=1$, we observe that the maximum jet height decreases with increasing ![]() $\beta$. This implies that the transition boundary (orange boundary along
$\beta$. This implies that the transition boundary (orange boundary along ![]() ${{\textit {De}}}$) shifts downward as
${{\textit {De}}}$) shifts downward as ![]() $\beta$ increases and upwards as
$\beta$ increases and upwards as ![]() $\beta$ decreases.
$\beta$ decreases.
Finally, we turn our attention to the transition between the droplet formation regime and the no-jet regime for ![]() ${{\textit {De}}} \sim O(10^{-2})$ (which corresponds to the green boundary along
${{\textit {De}}} \sim O(10^{-2})$ (which corresponds to the green boundary along ![]() $\mathcal {J}$ in figure 4). From (3.1), the apparent viscosity increases with decreasing
$\mathcal {J}$ in figure 4). From (3.1), the apparent viscosity increases with decreasing ![]() $\beta$, resulting in the transition from droplet formation to no-pinch-off occurring at lower
$\beta$, resulting in the transition from droplet formation to no-pinch-off occurring at lower ![]() $\mathcal {J}$ for decreasing
$\mathcal {J}$ for decreasing ![]() $\beta$. Consequently, this shifts the (green) boundary (along
$\beta$. Consequently, this shifts the (green) boundary (along ![]() $\mathcal {J}$) to lower
$\mathcal {J}$) to lower ![]() $\mathcal {J}$, as
$\mathcal {J}$, as ![]() ${{\textit {Oh}}}_p$ increases.
${{\textit {Oh}}}_p$ increases.
3.7. Energy analysis
The total energy in the computational domain at any time ![]() $t$ is composed of kinetic energy
$t$ is composed of kinetic energy ![]() $(E_k(t))$, surface energy (
$(E_k(t))$, surface energy (![]() $E_s(t)$, assuming flat free-surface to have zero surface energy), elastic energy
$E_s(t)$, assuming flat free-surface to have zero surface energy), elastic energy ![]() $(E_e)$ and, as well as energy dissipation due to both solvent viscosity
$(E_e)$ and, as well as energy dissipation due to both solvent viscosity ![]() $(E_d^s(t))$ and polymer relaxation
$(E_d^s(t))$ and polymer relaxation ![]() $(E_d^p(t))$. The miscellaneous energy due to the motion of air, jet breakup, etc. is represented by
$(E_d^p(t))$. The miscellaneous energy due to the motion of air, jet breakup, etc. is represented by ![]() $E_m(t)$. The time-evolution of the energy in the system is expressed as
$E_m(t)$. The time-evolution of the energy in the system is expressed as
The system's initial energy at ![]() $t = 0$ consists entirely of surface energy,
$t = 0$ consists entirely of surface energy, ![]() $E_i = E_s(0)$. We extend the energy analysis for Oldroyd-B viscoelastic fluids by Snoeijer et al. (Reference Snoeijer, Pandey, Herrada and Eggers2020) to derive the energy budget for the EVP fluid governed by Saramito (Reference Saramito2007)'s model. Appendix E provides a detailed derivation of this budget.
$E_i = E_s(0)$. We extend the energy analysis for Oldroyd-B viscoelastic fluids by Snoeijer et al. (Reference Snoeijer, Pandey, Herrada and Eggers2020) to derive the energy budget for the EVP fluid governed by Saramito (Reference Saramito2007)'s model. Appendix E provides a detailed derivation of this budget.
Figure 17 illustrates the energy budgets for four representative cases, each normalized by the initial energy ![]() $E_i$. These cases correspond to different regimes in the plastocapillary number
$E_i$. These cases correspond to different regimes in the plastocapillary number ![]() $\mathcal {J}$ and Deborah number
$\mathcal {J}$ and Deborah number ![]() ${{\textit {De}}}$ parameter space, as discussed in § 3.2. The figure shows the temporal evolution of various energy transfer modes. As the EVP fluid deforms, surface energy converts into kinetic energy. This deformation induces viscous dissipation due to the solvent viscosity component. Additionally, relaxing elastic stresses contribute to energy dissipation (
${{\textit {De}}}$ parameter space, as discussed in § 3.2. The figure shows the temporal evolution of various energy transfer modes. As the EVP fluid deforms, surface energy converts into kinetic energy. This deformation induces viscous dissipation due to the solvent viscosity component. Additionally, relaxing elastic stresses contribute to energy dissipation (![]() $E_d^p(t)$). However, the EVP fluid can store some energy as elastic energy (
$E_d^p(t)$). However, the EVP fluid can store some energy as elastic energy (![]() $E_e(t)$), potentially recoverable later in the bubble-bursting process.
$E_e(t)$), potentially recoverable later in the bubble-bursting process.

Figure 17. Energy budget for the bubble bursting in an EVP medium. The plots indicate the variation of different modes of energy transfer with respect to time for (a) ![]() $\mathcal {J}=0.1,{{\textit {De}}}=0.02$, (b)
$\mathcal {J}=0.1,{{\textit {De}}}=0.02$, (b) ![]() $\mathcal {J}=1,{{\textit {De}}}=0.01$, (c)
$\mathcal {J}=1,{{\textit {De}}}=0.01$, (c) ![]() $\mathcal {J}=0.1,{{\textit {De}}}=1$, (d)
$\mathcal {J}=0.1,{{\textit {De}}}=1$, (d) ![]() $\mathcal {J}=1,{{\textit {De}}}=20$.
$\mathcal {J}=1,{{\textit {De}}}=20$.
3.7.1. Droplet formation regime, Droplet–A (low elastic stress relaxation time and yield-stress limit,  $\mathcal {J} \rightarrow 0,\,{{\textit {De}}}\rightarrow 0$)
$\mathcal {J} \rightarrow 0,\,{{\textit {De}}}\rightarrow 0$)
Figure 17(a) depicts the temporal energy budget for low ![]() ${{\textit {De}}}$ and
${{\textit {De}}}$ and ![]() $\mathcal {J}$ values. The collapse of the high-energy bubble cavity initiates a cascade of energy conversions characterizing the early stages of bubble bursting. As the cavity collapses and capillary waves propagate (
$\mathcal {J}$ values. The collapse of the high-energy bubble cavity initiates a cascade of energy conversions characterizing the early stages of bubble bursting. As the cavity collapses and capillary waves propagate (![]() $t \lessapprox 0.5$), the initial surface energy
$t \lessapprox 0.5$), the initial surface energy ![]() $E_s(0)$ is released, increasing the fluid's kinetic energy
$E_s(0)$ is released, increasing the fluid's kinetic energy ![]() $E_k(t)$. Significant velocity gradients lead to viscous dissipation
$E_k(t)$. Significant velocity gradients lead to viscous dissipation ![]() $E_d^s(t)$ due to solvent viscous stresses, while the short relaxation time of elastic stresses causes a progressive increase in
$E_d^s(t)$ due to solvent viscous stresses, while the short relaxation time of elastic stresses causes a progressive increase in ![]() $E_d^p(t)$. Initially, solvent viscous stresses dominate, resulting in higher viscous dissipation compared with polymeric dissipation and elastic energy, despite
$E_d^p(t)$. Initially, solvent viscous stresses dominate, resulting in higher viscous dissipation compared with polymeric dissipation and elastic energy, despite ![]() ${{\textit {Oh}}}_p={{\textit {Oh}}}_s=0.5{{\textit {Oh}}}$.
${{\textit {Oh}}}_p={{\textit {Oh}}}_s=0.5{{\textit {Oh}}}$.
The ![]() $E_k(t)$ reaches its maximum when capillary waves focus at the cavity bottom, creating a high-velocity region. As these waves merge to form a jet, elastic energy
$E_k(t)$ reaches its maximum when capillary waves focus at the cavity bottom, creating a high-velocity region. As these waves merge to form a jet, elastic energy ![]() $E_e(t)$ is briefly stored and rapidly released as
$E_e(t)$ is briefly stored and rapidly released as ![]() $E_d^p(t)$ due to small
$E_d^p(t)$ due to small ![]() ${{\textit {De}}}$. The EVP fluid consistently stores more elastic energy as the jet develops, attributed to large axial elastic stresses in the jet and extra stress in both yielded and unyielded regions (see figure 5b). The jet-development process is characterized by substantial energy dissipation. Cumulative solvent viscous and polymer dissipation critically regulate jet growth and maximum height. The elastic energy at jet initiation is also crucial, as discussed in Appendix F.
${{\textit {De}}}$. The EVP fluid consistently stores more elastic energy as the jet develops, attributed to large axial elastic stresses in the jet and extra stress in both yielded and unyielded regions (see figure 5b). The jet-development process is characterized by substantial energy dissipation. Cumulative solvent viscous and polymer dissipation critically regulate jet growth and maximum height. The elastic energy at jet initiation is also crucial, as discussed in Appendix F.
To approach the final stoppage time of bubble bursting dynamics in an EVP fluid, the rate of change of different energy transfer modes must be negligible. However, at ![]() $t=1.2$, the surface energy remains non-zero and decreasing. Capturing a steady final state would require significantly longer simulation times, likely of the order of
$t=1.2$, the surface energy remains non-zero and decreasing. Capturing a steady final state would require significantly longer simulation times, likely of the order of ![]() $t \sim O(10)$, which is beyond the scope of this study. For low
$t \sim O(10)$, which is beyond the scope of this study. For low ![]() ${{\textit {De}}}$, viscoelastic solid-like deformation in the unyielded region will lead to elastic stress enervation, and the cavity is expected to approach a flat free interface.
${{\textit {De}}}$, viscoelastic solid-like deformation in the unyielded region will lead to elastic stress enervation, and the cavity is expected to approach a flat free interface.
3.7.2. No-jet regime (viscoplastic limit,  $\mathcal {J} \gg 0,{{\textit {De}}}\rightarrow 0$)
$\mathcal {J} \gg 0,{{\textit {De}}}\rightarrow 0$)
At extremely large ![]() $\mathcal {J}$ values, most of the domain remains unyielded. In this regime, Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021) observed finite
$\mathcal {J}$ values, most of the domain remains unyielded. In this regime, Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021) observed finite ![]() $E_s(t \to \infty )$ as the cavity shape remained invariant, accompanied by a decrease in kinetic energy and total viscous dissipation. In contrast, our study reveals that at low
$E_s(t \to \infty )$ as the cavity shape remained invariant, accompanied by a decrease in kinetic energy and total viscous dissipation. In contrast, our study reveals that at low ![]() ${{\textit {De}}}$, the viscoelastic deformation of the unyielded EVP fluid maintains cavity motion (see figure 7), resulting in a gradual decrease of surface energy over time. Figure 17(b) exemplifies this behaviour with a consistent interplay between
${{\textit {De}}}$, the viscoelastic deformation of the unyielded EVP fluid maintains cavity motion (see figure 7), resulting in a gradual decrease of surface energy over time. Figure 17(b) exemplifies this behaviour with a consistent interplay between ![]() $E_e(t)$ and
$E_e(t)$ and ![]() $E_d^p(t)$. Figure 17(b) also shows that at higher
$E_d^p(t)$. Figure 17(b) also shows that at higher ![]() $\mathcal {J}$ and lower
$\mathcal {J}$ and lower ![]() ${{\textit {De}}}$, the peak kinetic energy during capillary wave convergence reaches only
${{\textit {De}}}$, the peak kinetic energy during capillary wave convergence reaches only ![]() $\sim 30\,\%$ of the initial total energy, compared with
$\sim 30\,\%$ of the initial total energy, compared with ![]() $>40\,\%$ in other regimes. Further reduction in
$>40\,\%$ in other regimes. Further reduction in ![]() ${{\textit {De}}}$ (at sufficiently high
${{\textit {De}}}$ (at sufficiently high ![]() $\mathcal {J}$ and fixed
$\mathcal {J}$ and fixed ![]() ${{\textit {Oh}}}$) would lead to even lower kinetic energy and the formation of a non-flat equilibrium shape characteristic of bubble bursting in viscoplastic fluids. This occurs due to a large elastocapillary number
${{\textit {Oh}}}$) would lead to even lower kinetic energy and the formation of a non-flat equilibrium shape characteristic of bubble bursting in viscoplastic fluids. This occurs due to a large elastocapillary number ![]() $Ec = {{\textit {Oh}}}_p/{{\textit {De}}}$, resulting in a balance between elastic and surface stresses.
$Ec = {{\textit {Oh}}}_p/{{\textit {De}}}$, resulting in a balance between elastic and surface stresses.
3.7.3. No pinch-off regime (viscoelastocapillary limit,  ${{\textit {De}}} \sim O(1)$)
${{\textit {De}}} \sim O(1)$)
In the viscoelastocapillary regime, elastic stresses play a minimal role (![]() $E_e(t) \approx E_d^p(t) \approx 0$, figure 17c) during the initial bubble bursting in EVP fluid exemplified with
$E_e(t) \approx E_d^p(t) \approx 0$, figure 17c) during the initial bubble bursting in EVP fluid exemplified with ![]() $\mathcal {J}=0.1$. Nevertheless, the strength of the strongest capillary wave increases with Deborah number, as detailed in § 3.4. At the moment of capillary wave convergence, significant elastic energy storage and release occurs in the EVP fluid, facilitating jet formation. In this regime, elastic energy storage primarily originates from the Kelvin–Voigt viscoelastic solid region, sustaining elongational stress in the jet. As elastic stress in the jet's axial region intensifies and subsequently relaxes, figure 17(c) reveals a consistent increase in polymeric dissipation beyond
$\mathcal {J}=0.1$. Nevertheless, the strength of the strongest capillary wave increases with Deborah number, as detailed in § 3.4. At the moment of capillary wave convergence, significant elastic energy storage and release occurs in the EVP fluid, facilitating jet formation. In this regime, elastic energy storage primarily originates from the Kelvin–Voigt viscoelastic solid region, sustaining elongational stress in the jet. As elastic stress in the jet's axial region intensifies and subsequently relaxes, figure 17(c) reveals a consistent increase in polymeric dissipation beyond ![]() $t \approx 0.5$.
$t \approx 0.5$.
3.7.4. Droplet formation regime, Droplet–B (Newtonian-like limit,  ${{\textit {De}}}\gg 1$)
${{\textit {De}}}\gg 1$)
The energy transfer modes in this limit (figure 17d) closely resemble those observed in the viscoelastocapillary limit (figure 17c), with negligible elastic energy storage and polymeric dissipation (![]() $E_e(t) \approx E_d^p(t) \approx 0$) during the initial bubble bursting in EVP fluid. Additionally, this regime exhibits minimal elastic energy and polymeric dissipation during jet formation as well. These characteristics align with the Newtonian-like limit described by França et al. (Reference França, Jalaal and Oishi2024). Notably, for sufficiently large Deborah numbers (
$E_e(t) \approx E_d^p(t) \approx 0$) during the initial bubble bursting in EVP fluid. Additionally, this regime exhibits minimal elastic energy and polymeric dissipation during jet formation as well. These characteristics align with the Newtonian-like limit described by França et al. (Reference França, Jalaal and Oishi2024). Notably, for sufficiently large Deborah numbers (![]() ${{\textit {De}}}$), regardless of the plastocapillary number (
${{\textit {De}}}$), regardless of the plastocapillary number (![]() $\mathcal {J}$), elastic stresses become insignificant due to vanishing elastocapillary number (
$\mathcal {J}$), elastic stresses become insignificant due to vanishing elastocapillary number (![]() $Ec$) at finite solvent and polymeric Ohnesorge numbers (
$Ec$) at finite solvent and polymeric Ohnesorge numbers (![]() ${{\textit {Oh}}}_s, {{\textit {Oh}}}_p$) (also see § 3.2.4).
${{\textit {Oh}}}_s, {{\textit {Oh}}}_p$) (also see § 3.2.4).
In summary, this section examines the energy budget during bubble bursting in an EVP fluid across various regimes defined by the plastocapillary number ![]() $\mathcal {J}$ and Deborah number
$\mathcal {J}$ and Deborah number ![]() ${{\textit {De}}}$. The analysis reveals a complex interplay between surface energy, kinetic energy, elastic energy storage and dissipation mechanisms. In the droplet formation regime (low
${{\textit {De}}}$. The analysis reveals a complex interplay between surface energy, kinetic energy, elastic energy storage and dissipation mechanisms. In the droplet formation regime (low ![]() $\mathcal {J}$ and
$\mathcal {J}$ and ![]() ${{\textit {De}}}$), initial surface energy rapidly converts to kinetic energy and dissipation, with solvent viscous stresses dominating early stages despite equal solvent and polymeric Ohnesorge numbers. As
${{\textit {De}}}$), initial surface energy rapidly converts to kinetic energy and dissipation, with solvent viscous stresses dominating early stages despite equal solvent and polymeric Ohnesorge numbers. As ![]() $\mathcal {J}$ increases and
$\mathcal {J}$ increases and ![]() ${{\textit {De}}}$ decreases, the no-jet regime emerges, characterized by lower peak kinetic energy and persistent cavity motion due to viscoelastic deformation. The viscoelastocapillary limit (
${{\textit {De}}}$ decreases, the no-jet regime emerges, characterized by lower peak kinetic energy and persistent cavity motion due to viscoelastic deformation. The viscoelastocapillary limit (![]() ${{\textit {De}}} \sim O(1)$) exhibits minimal elastic effects initially, but significant elastic energy storage during jet formation. In the Newtonian-like limit (
${{\textit {De}}} \sim O(1)$) exhibits minimal elastic effects initially, but significant elastic energy storage during jet formation. In the Newtonian-like limit (![]() ${{\textit {De}}} \gg 1$), elastic effects become negligible throughout the process. Across all regimes, the dynamics of an EVP fluid exemplify a strong
${{\textit {De}}} \gg 1$), elastic effects become negligible throughout the process. Across all regimes, the dynamics of an EVP fluid exemplify a strong ![]() ${{\textit {De}}}$-dependent relationship between viscous and polymeric dissipation. Viscous dissipation increases with
${{\textit {De}}}$-dependent relationship between viscous and polymeric dissipation. Viscous dissipation increases with ![]() ${{\textit {De}}}$, while polymeric dissipation becomes more significant at lower
${{\textit {De}}}$, while polymeric dissipation becomes more significant at lower ![]() ${{\textit {De}}}$ values, proportional to
${{\textit {De}}}$ values, proportional to ![]() ${{\textit {De}}}^{-2}$ (for fixed
${{\textit {De}}}^{-2}$ (for fixed ![]() $\mathrm {tr}(\boldsymbol {A} - \boldsymbol {I})$ and
$\mathrm {tr}(\boldsymbol {A} - \boldsymbol {I})$ and ![]() ${{\textit {Oh}}}_p$). The polymeric dissipation, given by
${{\textit {Oh}}}_p$). The polymeric dissipation, given by
is confined to the yielded region of the fluid (![]() $K \ne 0$). In contrast, elastic energy storage occurs in both yielded and unyielded regions. Solvent viscous dissipation
$K \ne 0$). In contrast, elastic energy storage occurs in both yielded and unyielded regions. Solvent viscous dissipation ![]() $E_d^s$ also manifests in both regions; in the unyielded region, it arises from the Kelvin–Voigt solid behaviour where
$E_d^s$ also manifests in both regions; in the unyielded region, it arises from the Kelvin–Voigt solid behaviour where ![]() $\|\boldsymbol {\mathcal {D}}\| \ne 0$, resulting in dissipation.
$\|\boldsymbol {\mathcal {D}}\| \ne 0$, resulting in dissipation.
4. Conclusions and outlook
In this study, we investigate the bubble-bursting phenomenon using direct numerical simulations in an EVP medium to understand the interplay of elasticity (more particularly the elastic stress relaxation time characterized by ![]() ${{\textit {De}}}$) and plasticity (identified by
${{\textit {De}}}$) and plasticity (identified by ![]() $\mathcal {J}$) on the bursting mechanism. We observed distinct behaviours in the development of the jet depending on the control parameters
$\mathcal {J}$) on the bursting mechanism. We observed distinct behaviours in the development of the jet depending on the control parameters ![]() ${{\textit {De}}}$ and
${{\textit {De}}}$ and ![]() $\mathcal {J}$ of an EVP fluid, resulting in four main regimes.
$\mathcal {J}$ of an EVP fluid, resulting in four main regimes.
(i) Droplet formation regime, Droplet–A (low elastic stress relaxation time and yield-stress limit,
 $\mathcal {J} \rightarrow 0, {{\textit {De}}}\rightarrow 0$). This regime is characterized by a Newtonian-like jet growth and droplet formation. In this regime, due to the faster relaxation of elastic stresses, the resulting capillary stresses lead to the formation of a jet despite a higher elastocapillary number. Further, the fast decay of elastic stresses cannot suppress the droplet formation due to the Rayleigh–Plateau instability. In this Newtonian-like limit, increasing
$\mathcal {J} \rightarrow 0, {{\textit {De}}}\rightarrow 0$). This regime is characterized by a Newtonian-like jet growth and droplet formation. In this regime, due to the faster relaxation of elastic stresses, the resulting capillary stresses lead to the formation of a jet despite a higher elastocapillary number. Further, the fast decay of elastic stresses cannot suppress the droplet formation due to the Rayleigh–Plateau instability. In this Newtonian-like limit, increasing  ${{\textit {De}}}$ reduces the maximum jet height due to slower relaxation of elastic stresses and thereby an increase in the elastic energy at the time of jet initiation (see Appendix F).
${{\textit {De}}}$ reduces the maximum jet height due to slower relaxation of elastic stresses and thereby an increase in the elastic energy at the time of jet initiation (see Appendix F).(ii) No-jet regime (viscoplastic limit,
 $\mathcal {J} \gg 0,{{\textit {De}}}\rightarrow 0$). In this regime, the EVP fluid behaves similarly to a viscoplastic fluid. This regime is characterized by the absence of jet formation due to the increased apparent viscosity, which dampens capillary wave motion and suppresses jet initiation. Although the fluid remains mostly unyielded, exhibiting Kelvin–Voigt viscoelastic solid behaviour, it can slowly deform over time depending on the elastocapillary number. This behaviour contrasts with purely viscoplastic fluids, where non-flat final equilibrium shapes are retained due to the stored surface energy because of rigid behaviour in the unyielded region.
$\mathcal {J} \gg 0,{{\textit {De}}}\rightarrow 0$). In this regime, the EVP fluid behaves similarly to a viscoplastic fluid. This regime is characterized by the absence of jet formation due to the increased apparent viscosity, which dampens capillary wave motion and suppresses jet initiation. Although the fluid remains mostly unyielded, exhibiting Kelvin–Voigt viscoelastic solid behaviour, it can slowly deform over time depending on the elastocapillary number. This behaviour contrasts with purely viscoplastic fluids, where non-flat final equilibrium shapes are retained due to the stored surface energy because of rigid behaviour in the unyielded region.(iii) No pinch-off regime (viscoelastocapillary limit,
 ${{\textit {De}}} \sim O(1)$). In this regime, jet formation occurs without subsequent droplet generation. This regime is marked by a balance between elastic stresses and capillary forces, influenced by the slower relaxation time of elastic stresses. As a result, the jet grows consistently but does not break into droplets. Notably, plasticity has minimal impact on bubble bursting dynamics due to the lower elastocapillary number. The elastic energy and polymer dissipation decrease with increasing
${{\textit {De}}} \sim O(1)$). In this regime, jet formation occurs without subsequent droplet generation. This regime is marked by a balance between elastic stresses and capillary forces, influenced by the slower relaxation time of elastic stresses. As a result, the jet grows consistently but does not break into droplets. Notably, plasticity has minimal impact on bubble bursting dynamics due to the lower elastocapillary number. The elastic energy and polymer dissipation decrease with increasing  ${{\textit {De}}}$, leading to higher maximum jet heights, indicating that slower elastic stress relaxation contributes to more pronounced jet formation.
${{\textit {De}}}$, leading to higher maximum jet heights, indicating that slower elastic stress relaxation contributes to more pronounced jet formation.(iv) Droplet formation regime, Droplet–B (Newtonian-like limit,
 ${{\textit {De}}}\gg 1$). In this regime, the behaviour of the EVP fluid resembles a Newtonian-like fluid, with the jet eventually thinning and pinching off from its base. In this regime, most of the EVP fluid exhibits unyielded Kelvin–Voigt viscoelastic solid behaviour, due to low elastocapillary number. The low elastic stresses are unable to prevent the formation of the Worthington jet. The resulting jet experiences significant axial stress, which causes it to yield, leading to progressive thinning and eventual breakup at its base. Notably, the absence of substantial EVP stress relaxation in this regime makes polymeric dissipation a negligible factor. The influence of solvent–polymer viscosity ratio was also investigated in this study, where we showed increasing
${{\textit {De}}}\gg 1$). In this regime, the behaviour of the EVP fluid resembles a Newtonian-like fluid, with the jet eventually thinning and pinching off from its base. In this regime, most of the EVP fluid exhibits unyielded Kelvin–Voigt viscoelastic solid behaviour, due to low elastocapillary number. The low elastic stresses are unable to prevent the formation of the Worthington jet. The resulting jet experiences significant axial stress, which causes it to yield, leading to progressive thinning and eventual breakup at its base. Notably, the absence of substantial EVP stress relaxation in this regime makes polymeric dissipation a negligible factor. The influence of solvent–polymer viscosity ratio was also investigated in this study, where we showed increasing  ${{\textit {Oh}}}_p$ leads to a reduction of the maximum jet height. Additionally, a thicker jet was observed due to increased extensional viscosity in the EVP fluid.
${{\textit {Oh}}}_p$ leads to a reduction of the maximum jet height. Additionally, a thicker jet was observed due to increased extensional viscosity in the EVP fluid.
In summary, this study investigates the bubble-bursting dynamics in an EVP fluid, elucidating the nuanced effects of elastic stress relaxation and plasticity across varying Deborah and plastocapillary numbers. This investigation is particularly pertinent to industrial scenarios involving bubble interactions with complex fluids’ free surfaces. Our findings, bridging numerical simulations with potential experimental validations (Ji et al. Reference Ji, Yang, Wang, Ewoldt and Feng2023; Rodríguez-Díaz et al. Reference Rodríguez-Díaz, Rubio, Montanero, Gañán-Calvo and Cabezas2023), could further enhance the understanding of initial shape variations and bubble buoyancy in different fluids (Deoclecio et al. Reference Deoclecio, Soares and Popinet2023). While this study primarily focuses on elastic stress relaxation and yield stress effects, future work could incorporate additional complexities like the shear-dependent behaviour of EVP fluids for a more exhaustive understanding (Brown & Jaeger Reference Brown and Jaeger2014; Rosti et al. Reference Rosti, Izbassarov, Tammisola, Hormozi and Brandt2018). Overall, this research sheds light on the critical interplay of surface tension, elasticity and plasticity in shaping the bubble-bursting phenomenon in complex fluidic environments.
Acknowledgements
The simulations were run with the computational resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS).
Funding
This work is supported by the funding provided by the European Research Council grant no. 2021-StG-852529, MUCUS and the Swedish Research Council through grant no. 2021-04820. R.V. acknowledges the ERC grant no. 2021-CoG-101043998, DEEPCONTROL. V.S. acknowledges the financial support from the Physics of Fluids at the University of Twente under the FIP-II project, sponsored by NWO and Canon. M.J. acknowledges the ERC grant no. 2023-StG-101117025, FluMAB and funding by the NWO (Dutch Research Council) under the MIST (Mitigation Strategies for Airborne Infection Control) program. Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them.
Declaration of interests
The authors report no conflict of interest.
Data availability statement
The data that support the findings of this study are openly available on GitHub – Balasubramanian (Reference Balasubramanian2023).
Appendix A. Non-dimensionalization of governing equations
The governing equations for an incompressible fluid are
where ![]() $\rho _l$ is the density of the fluid,
$\rho _l$ is the density of the fluid, ![]() $\boldsymbol {u}$ is the velocity vector and
$\boldsymbol {u}$ is the velocity vector and ![]() $t$,
$t$, ![]() $p$ corresponds to the time and pressure, respectively. The deviatoric viscous stress tensor and the polymeric stress tensor are represented by
$p$ corresponds to the time and pressure, respectively. The deviatoric viscous stress tensor and the polymeric stress tensor are represented by ![]() $\boldsymbol {\tau _s}$ and
$\boldsymbol {\tau _s}$ and ![]() $\boldsymbol {\tau _p}$, respectively, and
$\boldsymbol {\tau _p}$, respectively, and ![]() $g$ corresponds to the acceleration due to gravity. The deviatoric viscous stress tensor is expressed as
$g$ corresponds to the acceleration due to gravity. The deviatoric viscous stress tensor is expressed as
where ![]() $\mu _s$ is the solvent viscosity and
$\mu _s$ is the solvent viscosity and ![]() $\boldsymbol {\mathcal {D}}$ is the deformation-rate tensor.
$\boldsymbol {\mathcal {D}}$ is the deformation-rate tensor.
According to the thermodynamically consistent constitutive relationship proposed by Saramito (Reference Saramito2007) for EVP fluid, the polymeric stress tensor evolves following the partial differential equation given by
where, ![]() $\lambda$ indicates the relaxation time of the polymers and
$\lambda$ indicates the relaxation time of the polymers and ![]() $\mu _p$,
$\mu _p$, ![]() $\tau _y$ corresponds to the polymer viscosity and yield stress of the fluid, respectively. Here,
$\tau _y$ corresponds to the polymer viscosity and yield stress of the fluid, respectively. Here, ![]() $\boldsymbol {\overset {\nabla }{\tau }_p}$ is the upper-convected time derivative and
$\boldsymbol {\overset {\nabla }{\tau }_p}$ is the upper-convected time derivative and ![]() $\|\boldsymbol {\tau _d}\|$ is the second invariant of the deviatoric part of the polymeric stress tensor
$\|\boldsymbol {\tau _d}\|$ is the second invariant of the deviatoric part of the polymeric stress tensor ![]() $\boldsymbol {\tau _p}$.
$\boldsymbol {\tau _p}$.
For our simulations, we consider the inertia-capillary velocity ![]() $(V_\gamma )$, initial bubble radius
$(V_\gamma )$, initial bubble radius ![]() $(R_0)$, inertial-capillary time
$(R_0)$, inertial-capillary time ![]() $(T_\gamma )$ and the capillary stress
$(T_\gamma )$ and the capillary stress ![]() $(p_\gamma )$ to non-dimensionalize the (A1)–(A4) resulting in non-dimensional equations (2.1), (2.2) and (2.15). The above-described quantities are defined as
$(p_\gamma )$ to non-dimensionalize the (A1)–(A4) resulting in non-dimensional equations (2.1), (2.2) and (2.15). The above-described quantities are defined as
 \begin{gather}T_\gamma = \frac{R_0}{V_\gamma} = \sqrt{\frac{\rho_l R_0^3}{\gamma}}, \end{gather}
\begin{gather}T_\gamma = \frac{R_0}{V_\gamma} = \sqrt{\frac{\rho_l R_0^3}{\gamma}}, \end{gather}The set of (A1)–(A3) are also solved for the gas phase with density ![]() $\rho _g$, viscosity
$\rho _g$, viscosity ![]() $\mu _g$ and no extra-stress tensor (
$\mu _g$ and no extra-stress tensor (![]() $\boldsymbol {\tau _p} = \boldsymbol {0}$).
$\boldsymbol {\tau _p} = \boldsymbol {0}$).
Appendix B. Log-conformation approach
In the present study, the effect of elasticity and plasticity embedded in an EVP fluid is modelled with the constitutive equation proposed by Saramito (Reference Saramito2007) as
In the above model, the unyielded fluid behaves as a Kelvin–Voigt solid whereas the yielded fluid flows as an Oldroyd-B viscoelastic fluid. The polymeric stress can be written in conformation tensor form as
where, ![]() $\boldsymbol {A}$ corresponds to the conformation tensor, an order parameter that keeps track of the stretching of the polymers (Snoeijer et al. Reference Snoeijer, Pandey, Herrada and Eggers2020; Stone et al. Reference Stone, Shelley and Boyko2023). Filling in (B2), (B1) can be rewritten as
$\boldsymbol {A}$ corresponds to the conformation tensor, an order parameter that keeps track of the stretching of the polymers (Snoeijer et al. Reference Snoeijer, Pandey, Herrada and Eggers2020; Stone et al. Reference Stone, Shelley and Boyko2023). Filling in (B2), (B1) can be rewritten as
with the switch-term ![]() $K = \max ((\|\boldsymbol {\tau _d}\|-\mathcal {J})/\|\boldsymbol {\tau _d}\|,0 )$.
$K = \max ((\|\boldsymbol {\tau _d}\|-\mathcal {J})/\|\boldsymbol {\tau _d}\|,0 )$.
In order to simulate high Deborah numbers, we use the log-conformation formulation (Fattal & Kupferman Reference Fattal and Kupferman2004) to preserve positive-definiteness of ![]() $\boldsymbol {A}$ and alleviate the high-Weissenberg-number problem.
$\boldsymbol {A}$ and alleviate the high-Weissenberg-number problem.
In the log-conformation formulation, the components of ![]() $\boldsymbol {A}$ in (B3) are solved using the split scheme approach similar to that of Hao & Pan (Reference Hao and Pan2007) in the basis of a logarithm of the conformation tensor as
$\boldsymbol {A}$ in (B3) are solved using the split scheme approach similar to that of Hao & Pan (Reference Hao and Pan2007) in the basis of a logarithm of the conformation tensor as ![]() $\boldsymbol {\psi } = \mathrm {log}\,\boldsymbol {A}$, since
$\boldsymbol {\psi } = \mathrm {log}\,\boldsymbol {A}$, since ![]() $\boldsymbol {A}$ is positive definite. The velocity gradient tensor
$\boldsymbol {A}$ is positive definite. The velocity gradient tensor ![]() $\boldsymbol {\nabla } \boldsymbol {u}$ is decomposed into two antisymmetric tensors
$\boldsymbol {\nabla } \boldsymbol {u}$ is decomposed into two antisymmetric tensors ![]() $\boldsymbol {\varOmega }$ and
$\boldsymbol {\varOmega }$ and ![]() $\boldsymbol {N}$, and a symmetric tensor
$\boldsymbol {N}$, and a symmetric tensor ![]() $\boldsymbol {B}$ such that
$\boldsymbol {B}$ such that ![]() $\boldsymbol {\nabla } \boldsymbol {u} = \boldsymbol {\varOmega } + \boldsymbol {N}\boldsymbol {A}^{-1} + \boldsymbol {B}$. Hence, (B3) in the log-conformation tensor formulation reads
$\boldsymbol {\nabla } \boldsymbol {u} = \boldsymbol {\varOmega } + \boldsymbol {N}\boldsymbol {A}^{-1} + \boldsymbol {B}$. Hence, (B3) in the log-conformation tensor formulation reads
The extra stress tensor ![]() $\boldsymbol {\tau _p}$ evolution is solved explicitly in time, with its divergence incorporated as a pressure-gradient-like source term in the momentum equation (A2). The explicit time-stepping for both
$\boldsymbol {\tau _p}$ evolution is solved explicitly in time, with its divergence incorporated as a pressure-gradient-like source term in the momentum equation (A2). The explicit time-stepping for both ![]() $\boldsymbol {\tau _p}$ evolution and surface tension necessitates a sufficiently small time step to maintain numerical stability. For the cases we have simulated, the capillary time step restriction (discussed in § 2.2 and Popinet (Reference Popinet2009)) proves limiting. The readers are referred to López-Herrera et al. (Reference López-Herrera, Popinet and Castrejón-Pita2019) for the corresponding implementation details in Basilisk C. Our implementation of the EVP model in Basilisk C can be found at Balasubramanian (Reference Balasubramanian2023).
$\boldsymbol {\tau _p}$ evolution and surface tension necessitates a sufficiently small time step to maintain numerical stability. For the cases we have simulated, the capillary time step restriction (discussed in § 2.2 and Popinet (Reference Popinet2009)) proves limiting. The readers are referred to López-Herrera et al. (Reference López-Herrera, Popinet and Castrejón-Pita2019) for the corresponding implementation details in Basilisk C. Our implementation of the EVP model in Basilisk C can be found at Balasubramanian (Reference Balasubramanian2023).
Appendix C. Grid-dependence study
Basilisk employs a quadtree grid system that enables resolutions in powers of 2, denoted as ![]() $2^n$. Given our chosen square computational domain of size
$2^n$. Given our chosen square computational domain of size ![]() $8R_0$, the number of uniform grid points across the initial bubble radius
$8R_0$, the number of uniform grid points across the initial bubble radius ![]() $R_0$ is
$R_0$ is ![]() $2^{n-3}$ and thereby the minimum cell size is
$2^{n-3}$ and thereby the minimum cell size is ![]() $\varDelta = 1/2^{n-3}$. In our study, we implement three different resolution levels:
$\varDelta = 1/2^{n-3}$. In our study, we implement three different resolution levels: ![]() $\varDelta = 1/2^{n-3}, 1/2^{n-4}$ and
$\varDelta = 1/2^{n-3}, 1/2^{n-4}$ and ![]() $1/2^{n-5}$, depending on the proximity to the bubble. Specifically, we use a grid resolution of
$1/2^{n-5}$, depending on the proximity to the bubble. Specifically, we use a grid resolution of ![]() $\varDelta = 1/2^{n-3}$ very close to the bubble
$\varDelta = 1/2^{n-3}$ very close to the bubble ![]() $(r<1.28 R_0)$ and
$(r<1.28 R_0)$ and ![]() $1/2^{n-5}$ near the boundary. Figure 18 demonstrates the grid size independence of the bubble bursting results in terms of jet development.
$1/2^{n-5}$ near the boundary. Figure 18 demonstrates the grid size independence of the bubble bursting results in terms of jet development.

Figure 18. Variation of the interface height at the axis for (a) ![]() $\mathcal {J}=0.01,{{\textit {De}}}=0.01$, (b)
$\mathcal {J}=0.01,{{\textit {De}}}=0.01$, (b) ![]() $\mathcal {J}=1.0,{{\textit {De}}}=16$ at different grid resolutions. Inset shows the liquid interface at (a) the drop formation time and (b) at around the maximum jet height.
$\mathcal {J}=1.0,{{\textit {De}}}=16$ at different grid resolutions. Inset shows the liquid interface at (a) the drop formation time and (b) at around the maximum jet height.
From figure 18, we see that the adaptive scheme yields similar results for ![]() $n=13,14$ at low
$n=13,14$ at low ![]() ${{\textit {De}}}$. For high values of elasticity, similar jet development is observed for
${{\textit {De}}}$. For high values of elasticity, similar jet development is observed for ![]() $n=14$ and
$n=14$ and ![]() $15$. It should be noted that the droplet breakup is mesh-size dependent (i.e. a droplet is formed when the thickness of the jet is smaller than the grid size) and hence, we have focused on a qualitative description of droplet breakup time rather than a quantitative study. Furthermore, we have observed that the difference in droplet breakup time does not significantly impact later jet development process, leading to grid-converged results. For higher
$15$. It should be noted that the droplet breakup is mesh-size dependent (i.e. a droplet is formed when the thickness of the jet is smaller than the grid size) and hence, we have focused on a qualitative description of droplet breakup time rather than a quantitative study. Furthermore, we have observed that the difference in droplet breakup time does not significantly impact later jet development process, leading to grid-converged results. For higher ![]() ${{\textit {De}}}$, given that the Oldroyd-B model allows for the buildup of infinite stress, we find that a sufficiently fine grid is necessary to accurately resolve the elastic stresses, which are predominantly concentrated in the axial region of the jet.
${{\textit {De}}}$, given that the Oldroyd-B model allows for the buildup of infinite stress, we find that a sufficiently fine grid is necessary to accurately resolve the elastic stresses, which are predominantly concentrated in the axial region of the jet.
Appendix D. Comparison of the Bingham model and EVP model at viscoplastic limit
The constitutive equation for a Bingham viscoplastic fluid (in non-dimensional form) is given by
 \begin{equation} \left. \begin{array}{ll} \boldsymbol{\mathcal{D}} = \boldsymbol{0} & \|\boldsymbol{\tau}\| < \mathcal{J},\\ \boldsymbol{\tau} = 2\left(\dfrac{\mathcal{J}}{2\|\boldsymbol{\mathcal{D}}\|} + {{\textit{Oh}}} \right)\boldsymbol{\mathcal{D}} & \|\boldsymbol{\tau}\| \ge \mathcal{J}\,. \end{array} \right\} \end{equation}
\begin{equation} \left. \begin{array}{ll} \boldsymbol{\mathcal{D}} = \boldsymbol{0} & \|\boldsymbol{\tau}\| < \mathcal{J},\\ \boldsymbol{\tau} = 2\left(\dfrac{\mathcal{J}}{2\|\boldsymbol{\mathcal{D}}\|} + {{\textit{Oh}}} \right)\boldsymbol{\mathcal{D}} & \|\boldsymbol{\tau}\| \ge \mathcal{J}\,. \end{array} \right\} \end{equation} With the introduction of a ‘large’ viscous regularization parameter ![]() ${{\textit {Oh}}}_{max}$ in (D1) for the unyielded state, the regularized Bingham model reads
${{\textit {Oh}}}_{max}$ in (D1) for the unyielded state, the regularized Bingham model reads
Nevertheless, the stress in the yielded region of viscoplastic liquid is
However, for the EVP model in this study, towards the viscoplastic limit (![]() ${{\textit {De}}} \rightarrow 0$) and specifically
${{\textit {De}}} \rightarrow 0$) and specifically ![]() ${{\textit {De}}}=0$ from (2.4) and (2.15), we obtain
${{\textit {De}}}=0$ from (2.4) and (2.15), we obtain
where the definition of ![]() $K$ from (2.8) for the yielded state of EVP fluid is used in (D6).
$K$ from (2.8) for the yielded state of EVP fluid is used in (D6).
From (D3) and (D6), we observe that the regularized Bingham model and EVP model can be equivalent if
The above equation holds for ![]() $\beta = 0$ and if the value of
$\beta = 0$ and if the value of ![]() $\beta = {{\textit {Oh}}}_s/{{\textit {Oh}}} > 0$, then the effective yielded viscosity in the EVP fluid is lower than that in the Bingham viscoplastic model.
$\beta = {{\textit {Oh}}}_s/{{\textit {Oh}}} > 0$, then the effective yielded viscosity in the EVP fluid is lower than that in the Bingham viscoplastic model.
Appendix E. Energy-budget calculation
The formulation for different modes of energy transfer is presented here. Similar energy-transfer mode calculations have been employed in prior works, such as Ramírez-Soto et al. (Reference Ramírez-Soto, Sanjay, Lohse, Pham and Vollmer2020) and Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021), for evaluating energy budgets in scenarios involving colliding droplets and bubble bursting, respectively. In our study, we extend this methodology to EVP liquids. Building upon the work by Snoeijer et al. (Reference Snoeijer, Pandey, Herrada and Eggers2020) in energy analysis for Oldroyd-B viscoelastic fluids, we adapt the formulation to EVP fluids.
From (2.2), the rate of change of kinetic energy can be written as
The terms in the square braces correspond to the energy flux terms and the last two terms in the above equation corresponds to work done due to solvent viscosity and polymers, respectively, and is written as
The work done due to polymers can be further split into
where ![]() $W$ is the elastic energy density and
$W$ is the elastic energy density and ![]() $\epsilon _p$ is the dissipation of energy due to polymers. It should be noted that the elastic energy is associated with the polymer elongation and thereby is a function of
$\epsilon _p$ is the dissipation of energy due to polymers. It should be noted that the elastic energy is associated with the polymer elongation and thereby is a function of ![]() $\mathrm {tr}(\boldsymbol {A})$. Similarly, the relaxation of elastic stresses (thereby relaxation of conformation tensor
$\mathrm {tr}(\boldsymbol {A})$. Similarly, the relaxation of elastic stresses (thereby relaxation of conformation tensor ![]() $\boldsymbol {\overset {\nabla }A}$) gives rise to polymer dissipation
$\boldsymbol {\overset {\nabla }A}$) gives rise to polymer dissipation ![]() $\epsilon _p$. Here,
$\epsilon _p$. Here, ![]() $\boldsymbol {\overset {\nabla }A}$ corresponds to the terms in the square braces of (B3).
$\boldsymbol {\overset {\nabla }A}$ corresponds to the terms in the square braces of (B3).
For an Oldroyd-B model, starting from the elastic stress evolution (B3) we have
with ![]() $K = 1$. Taking the trace of the constitutive equation, we arrive at the following expressions:
$K = 1$. Taking the trace of the constitutive equation, we arrive at the following expressions:
for elastic energy and polymer dissipation, respectively.
The key distinction between the viscoelastic Oldroyd-B model and the Saramito (Reference Saramito2007) model lies in the presence of the switch term ![]() $K$ (which mimics the effect of plasticity). It is straightforward to demonstrate that this switch term does not affect the elastic energy of the EVP fluid. The above conclusion is based on the definition that, before yielding of the EVP fluid, it behaves as a Kelvin–Voigt viscoelastic solid, which inherently includes the neo-Hookean spring. However, once the fluid has yielded, the polymer dissipation
$K$ (which mimics the effect of plasticity). It is straightforward to demonstrate that this switch term does not affect the elastic energy of the EVP fluid. The above conclusion is based on the definition that, before yielding of the EVP fluid, it behaves as a Kelvin–Voigt viscoelastic solid, which inherently includes the neo-Hookean spring. However, once the fluid has yielded, the polymer dissipation ![]() $\epsilon _p = f(\boldsymbol {\overset {\nabla }{A}})$ is identical to that in the Oldroyd-B model. The expressions for the elastic energy and polymer dissipation in an EVP are, respectively, given by
$\epsilon _p = f(\boldsymbol {\overset {\nabla }{A}})$ is identical to that in the Oldroyd-B model. The expressions for the elastic energy and polymer dissipation in an EVP are, respectively, given by
In § 3.7 we analyse the temporal evolution of energy within the computational domain, following a similar approach as used in Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021). The kinetic and the surface energy of the liquid are, respectively, given by
It should be noted that the energies are normalized by the surface energy ![]() $\gamma R_0^2$. The integrals for the energy in the fluid are evaluated over the volume (
$\gamma R_0^2$. The integrals for the energy in the fluid are evaluated over the volume (![]() $\varOmega$) and the surface (
$\varOmega$) and the surface (![]() $\varGamma$) of the largest liquid continuum in the computational domain and does not encompass the drops (which are constituted under a separate term
$\varGamma$) of the largest liquid continuum in the computational domain and does not encompass the drops (which are constituted under a separate term ![]() $E_m$). Furthermore, the state of the liquid pool, characterized by a flat free surface
$E_m$). Furthermore, the state of the liquid pool, characterized by a flat free surface ![]() $\zeta$ (
$\zeta$ (![]() $\mathcal {Z}=0$), is considered as the reference condition.
$\mathcal {Z}=0$), is considered as the reference condition.
The dissipation due to the solvent part of the EVP fluid is given by
The elastic energy and the polymer dissipation are quantified as
All other forms of energy is constituted as
In (E15) the superscript ‘Drops’ corresponds to the ejected drops with the corresponding volume denoted by ![]() $\varOmega _d$. Further, the terms in (E15), respectively, correspond to the kinetic energy, surface energy, viscous dissipation and polymer work in the drops. The volume integrals are performed in the same way as in (E10)–(E14) except that the integrals are performed over
$\varOmega _d$. Further, the terms in (E15), respectively, correspond to the kinetic energy, surface energy, viscous dissipation and polymer work in the drops. The volume integrals are performed in the same way as in (E10)–(E14) except that the integrals are performed over ![]() $\varOmega _d$. The last two terms in (E15) correspond to the gravitational potential for the fluid and the total energy stored in the gas phase, respectively.
$\varOmega _d$. The last two terms in (E15) correspond to the gravitational potential for the fluid and the total energy stored in the gas phase, respectively.
The total energy in the gas phase occupying a volume ![]() $\varOmega _g$, as outlined in Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021), is written as
$\varOmega _g$, as outlined in Sanjay et al. (Reference Sanjay, Lohse and Jalaal2021), is written as
 \begin{equation} E_g = \rho_r \int_{\varOmega_g} \left( \frac{\|\boldsymbol{u}\|^2}{2} + {\textit{Bo}} \mathcal{Z} \right) {\rm d}\varOmega_g + 2\mu_r {{\textit{Oh}}} \int_{t} \left( \int_{\varOmega_g} \| \boldsymbol{\mathcal{D}} \|^2\, {\rm d}\varOmega_g \right) \,{\rm d}t. \end{equation}
\begin{equation} E_g = \rho_r \int_{\varOmega_g} \left( \frac{\|\boldsymbol{u}\|^2}{2} + {\textit{Bo}} \mathcal{Z} \right) {\rm d}\varOmega_g + 2\mu_r {{\textit{Oh}}} \int_{t} \left( \int_{\varOmega_g} \| \boldsymbol{\mathcal{D}} \|^2\, {\rm d}\varOmega_g \right) \,{\rm d}t. \end{equation}Appendix F. Different jet growth at low  ${{\textit {De}}}$ and high
${{\textit {De}}}$ and high  ${{\textit {De}}}$
${{\textit {De}}}$
From figure 10(a), we observed that the jet height increases with ![]() ${{\textit {De}}}$ for
${{\textit {De}}}$ for ![]() ${{\textit {De}}}\sim O(1)$ in the viscoelastocapillary regime. In this section, we plot the temporal evolution of corresponding polymeric dissipation, ratio of polymeric dissipation to the total dissipation contribution from viscosity and polymers and elastic energy in figure 19(a–c), respectively. From figure 19(a), we observe that the polymeric dissipation during the jet development phase constitutes to only around 3 % of the total initial surface energy for
${{\textit {De}}}\sim O(1)$ in the viscoelastocapillary regime. In this section, we plot the temporal evolution of corresponding polymeric dissipation, ratio of polymeric dissipation to the total dissipation contribution from viscosity and polymers and elastic energy in figure 19(a–c), respectively. From figure 19(a), we observe that the polymeric dissipation during the jet development phase constitutes to only around 3 % of the total initial surface energy for ![]() ${{\textit {De}}}=1$ and decreases with increase in
${{\textit {De}}}=1$ and decreases with increase in ![]() ${{\textit {De}}}$. Viscous dissipation increases with
${{\textit {De}}}$. Viscous dissipation increases with ![]() ${{\textit {De}}}$ such that, the ratio of the polymeric dissipation to the total viscous and polymeric dissipation decreases with
${{\textit {De}}}$ such that, the ratio of the polymeric dissipation to the total viscous and polymeric dissipation decreases with ![]() ${{\textit {De}}}$, as observed in figure 19(b). In the considered range of De, the polymeric dissipation is less than 6 % in comparison with the total dissipation of energy in the system. Further, the elastic energy in the EVP fluid is more pronounced closer to
${{\textit {De}}}$, as observed in figure 19(b). In the considered range of De, the polymeric dissipation is less than 6 % in comparison with the total dissipation of energy in the system. Further, the elastic energy in the EVP fluid is more pronounced closer to ![]() $t\approx 0.5$–
$t\approx 0.5$–![]() $0.6$ as shown in figure 19(c), where the merged capillary waves result in jet formation. The corresponding decrease of elastic energy with increase in
$0.6$ as shown in figure 19(c), where the merged capillary waves result in jet formation. The corresponding decrease of elastic energy with increase in ![]() ${{\textit {De}}}$ is due to lower elastocapillary number. The elastic stresses are concentrated at a smaller region in the domain and hence, overall the elastic energy in the EVP fluid (because of unyielded region also) is decreasing with
${{\textit {De}}}$ is due to lower elastocapillary number. The elastic stresses are concentrated at a smaller region in the domain and hence, overall the elastic energy in the EVP fluid (because of unyielded region also) is decreasing with ![]() ${{\textit {De}}}$ at jet initiation. (Note that the unyielded region behaves as an elastic solid with low elastic modulus.) The combined effects of increasing viscous dissipation and decreasing polymer dissipation and elastic energy at jet initiation contributes to an increase in kinetic energy of the jet and thereby results in higher jet growth with respect to
${{\textit {De}}}$ at jet initiation. (Note that the unyielded region behaves as an elastic solid with low elastic modulus.) The combined effects of increasing viscous dissipation and decreasing polymer dissipation and elastic energy at jet initiation contributes to an increase in kinetic energy of the jet and thereby results in higher jet growth with respect to ![]() ${{\textit {De}}}$ in the viscoelastocapillary regime.
${{\textit {De}}}$ in the viscoelastocapillary regime.

Figure 19. Temporal variation of (a) polymeric dissipation, (b) ratio of polymeric dissipation to viscous and polymeric dissipation and (c) elastic energy, normalized with the initial energy for different ![]() ${{\textit {De}}}$ in the viscoelastocapillary regime at
${{\textit {De}}}$ in the viscoelastocapillary regime at ![]() $\mathcal {J}=0.1$.
$\mathcal {J}=0.1$.
Whereas in figure 10(b), the jet height is shown to decrease with ![]() ${{\textit {De}}}$ of the fluid for
${{\textit {De}}}$ of the fluid for ![]() ${{\textit {De}}}\sim O(0.01)$. In order to elucidate the different behaviour of jet growth, the corresponding temporal evolution of polymeric dissipation is plotted in figure 20(a). Here,
${{\textit {De}}}\sim O(0.01)$. In order to elucidate the different behaviour of jet growth, the corresponding temporal evolution of polymeric dissipation is plotted in figure 20(a). Here, ![]() ${{\textit {De}}}=0.01,0.02$ is not considered as they result in drop formation. The polymeric dissipation shows a decrease with increase in
${{\textit {De}}}=0.01,0.02$ is not considered as they result in drop formation. The polymeric dissipation shows a decrease with increase in ![]() ${{\textit {De}}}$, similar to the observation in figure 19(a). However, the magnitude of polymeric dissipation is considerably higher in comparison with that observed for
${{\textit {De}}}$, similar to the observation in figure 19(a). However, the magnitude of polymeric dissipation is considerably higher in comparison with that observed for ![]() ${{\textit {De}}}\sim O(1)$. This is due to higher elastocapillary number and thereby the elastic energy is larger with significant polymer dissipation (due to lower
${{\textit {De}}}\sim O(1)$. This is due to higher elastocapillary number and thereby the elastic energy is larger with significant polymer dissipation (due to lower ![]() ${{\textit {De}}}$). Further, the ratio of polymeric dissipation to total dissipation is plotted in figure 20(b), which indicates that the polymeric dissipation contributes to around 40 % of the total dissipation of energy. This is because of the larger yielded region at
${{\textit {De}}}$). Further, the ratio of polymeric dissipation to total dissipation is plotted in figure 20(b), which indicates that the polymeric dissipation contributes to around 40 % of the total dissipation of energy. This is because of the larger yielded region at ![]() ${{\textit {De}}}\sim O(0.01)$, where polymeric activity is pronounced. The variation of elastic energy with respect to
${{\textit {De}}}\sim O(0.01)$, where polymeric activity is pronounced. The variation of elastic energy with respect to ![]() ${{\textit {De}}}$ is shown in figure 20(c). The increasing elastic energy at the time of jet initiation (
${{\textit {De}}}$ is shown in figure 20(c). The increasing elastic energy at the time of jet initiation (![]() $t\approx 0.5$) is due to the increased storage of elastic energy both in the yielded region (where elastic stress is relaxing slower) and relatively larger unyielded region that exhibits solid behaviour (refer to figures 5b and 6b). The increase in elastic energy results in strain-rate hardening and thereby reduces the jet growth. Note that this variation in the elastic energy also affects the initiation kinetic energy of the jet and thereby the maximum initiation velocity of the jet. Further, the jet development is dictated by the capillary stresses and storage and relaxation of elastic stresses in the jet. Overall, the observation of lower maximum jet height with respect to
$t\approx 0.5$) is due to the increased storage of elastic energy both in the yielded region (where elastic stress is relaxing slower) and relatively larger unyielded region that exhibits solid behaviour (refer to figures 5b and 6b). The increase in elastic energy results in strain-rate hardening and thereby reduces the jet growth. Note that this variation in the elastic energy also affects the initiation kinetic energy of the jet and thereby the maximum initiation velocity of the jet. Further, the jet development is dictated by the capillary stresses and storage and relaxation of elastic stresses in the jet. Overall, the observation of lower maximum jet height with respect to ![]() ${{\textit {De}}}$ for
${{\textit {De}}}$ for ![]() ${{\textit {De}}}\sim O(0.01)$ is related to the elastic energy component of the EVP fluid.
${{\textit {De}}}\sim O(0.01)$ is related to the elastic energy component of the EVP fluid.

Figure 20. Temporal variation of (a) polymeric dissipation, (b) ratio of polymeric dissipation to viscous and polymeric dissipation and (c) elastic energy, normalized with the initial energy for low ![]() ${{\textit {De}}}$ and
${{\textit {De}}}$ and ![]() $\mathcal {J}=0.1$.
$\mathcal {J}=0.1$.






































































































