Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-27T12:28:14.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Buoyancy-induced turbulent mixing in a narrow tilted tank

Published online by Cambridge University Press:  20 May 2015

Tiras Y. Lin ,
C. P. Caulfield  and
Andrew W. Woods
Tiras Y. Lin
Affiliation:
BP Institute, University of Cambridge, Cambridge CB3 0EZ, UK Department of Earth Sciences, University of Cambridge, Cambridge CB2 3EQ, UK
C. P. Caulfield*
Affiliation:
BP Institute, University of Cambridge, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK
Andrew W. Woods
Affiliation:
BP Institute, University of Cambridge, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe a series of experiments in which a constant buoyancy flux 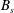$B_{s}$ of salty dyed water of density 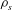${\it\rho}_{s}$ is introduced at the top of a long narrow tank of square cross-section tilted at an angle 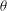${\it\theta}$ to the vertical. The tank is initially filled with fresh clear water of density 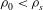${\it\rho}_{0}<{\it\rho}_{s}$, and we investigate the resulting buoyancy-driven turbulent mixing at various tilt angles 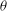${\it\theta}$. Using a light-attenuation image analysis method, we determine the evolution of the reduced gravity 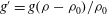$g^{\prime }=g({\it\rho}-{\it\rho}_{0})/{\it\rho}_{0}$ of the mixed fluid in time and space as it propagates towards the bottom of the tank. 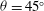For all tilt angles tested (${\it\theta}=0^{\circ }$ to ${\it\theta}=45^{\circ }$), we focus exclusively on high-Reynolds-number experiments, where the flow remains turbulent both along the length and across the width of the tank. We find that when 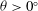${\it\theta}>0^{\circ }$, the cross-tank component of gravity acts to segregate the dense fluid from the relatively lighter fluid, and a statically stable gradient of 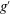$g^{\prime }$ across the width of the tank occurs more frequently than a statically unstable gradient, i.e. $(\partial g^{\prime }/\partial x)<0$ occurs more frequently than 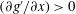$(\partial g^{\prime }/\partial x)>0$. This is in contrast to the case when 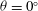${\it\theta}=0^{\circ }$, where instantaneous cross-tank gradients of reduced gravity may be positive or negative, but are equal to zero in an ensemble average. We observe that when 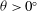${\it\theta}>0^{\circ }$, the cross-tank gradient of reduced gravity induces a turbulent counterflow where dense fluid flows down the upward-facing surface of the tank and lighter fluid flows in the opposing direction above. We model the evolution of the cross-tank averaged, ensemble averaged reduced gravity 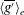$\langle \overline{g^{\prime }}\rangle _{e}$ as a diffusive process using Prandtl’s mixing length theory, building on the model of van Sommeren et al. (J. Fluid Mech., vol. 701, 2012, pp. 278–303) who considered purely vertical tanks. We model the fluctuations (from the cross-tank averaged quantity) of reduced gravity 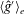$\langle {\hat{g}}^{\prime }\rangle _{e}$ and counterflow velocity 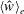$\langle {\hat{w}}\rangle _{e}$ by characterising the mixing across the width of the tank with a cross-tank turbulent diffusivity 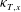${\it\kappa}_{T,x}$, which we assume is constant in the cross-tank coordinate $x$. We show that the counterflow that exists when 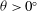${\it\theta}>0^{\circ }$ acts directly to enhance the effective along-tank turbulent diffusivity ${\it\kappa}_{T,z}$, and from experiments, we find that the mixing length increases approximately linearly with 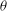${\it\theta}$, and that both 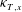${\it\kappa}_{T,x}$ and 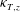${\it\kappa}_{T,z}$ are proportional to 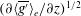$(\partial \langle \overline{g^{\prime }}\rangle _{e}/\partial z)^{1/2}$.

JFM classification

Turbulent Flows: Turbulent convection Turbulent Flows: Turbulent Flows Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 773 , 25 June 2015 , pp. 267 - 297
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baird, M. H. I., Aravamudan, K., Rao, N. V. R., Chadam, J. & Peirce, A. P. 1992 Unsteady axial mixing by natural convection in a vertical column. AIChE J. 38, 1825–1834.Google Scholar
Barnett, S.1991 The dynamics of buoyant releases in confined spaces. PhD thesis, University of Cambridge.Google Scholar
Britter, R. E. & Linden, P. F. 1980 The motion of the front of a gravity current travelling down an incline. J. Fluid Mech. 99, 531–543.CrossRefGoogle Scholar
Britter, R. E. & Simpson, J. E. 1978 Experiments on the dynamics of a gravity current head. J. Fluid Mech. 88, 223–240.CrossRefGoogle Scholar
Caulfield, C. P. & Woods, A. W. 1995 Plumes with non-monotonic mixing behaviour. Geophys. Astrophys. Fluid Dyn. 79 (1–4), 173–199.Google Scholar
Dalziel, S. B., Patterson, M. D., Caulfield, C. P. & Coomaraswamy, I. A. 2008 Mixing efficiency in high-aspect-ratio Rayleigh–Taylor experiments. Phys. Fluids 20 (6), 065106.CrossRefGoogle Scholar
Debacq, M., Fanguet, V., Hulin, J.-P., Salin, D. & Perrin, B. 2001 Self-similar concentration profiles in buoyant mixing of miscible fluids in a vertical tube. Phys. Fluids 13 (11), 3097–3100.Google Scholar
Debacq, M., Hulin, J.-P., Salin, D., Perrin, B. & Hinch, E. J. 2003 Buoyant mixing of miscible fluids of varying viscosities in vertical tubes. Phys. Fluids 15 (12), 3846–3855.CrossRefGoogle Scholar
Dhillon, B. S. 2010 Mine Safety: A Modern Approach. Springer.CrossRefGoogle Scholar
Fennell, D. 1988 Investigation into the King’s Cross Underground Fire. H.M.S.O.Google Scholar
Fragoso, A. T., Patterson, M. D. & Wettlaufer, J. S. 2013 Mixing in gravity currents. J. Fluid Mech. 734, 1–10.Google Scholar
Hallworth, M. A., Huppert, H. E., Phillips, J. C. & Sparks, R. S. J. 1996 Entrainment into two-dimensional and axisymmetric turbulent gravity currents. J. Fluid Mech. 308, 289–311.Google Scholar
Hallworth, M. A., Phillips, J. C., Huppert, H. E. & Sparks, R. S. J. 1993 Entrainment in turbulent gravity currents. Nature 362, 829–831.CrossRefGoogle Scholar
Holmes, T. L., Karr, A. E. & Baird, M. H. I. 1991 Effect of unfavorable continuous phase density gradient on axial mixing. AIChE J. 37 (3), 360–366.Google Scholar
Hunt, G. R. & Kaye, N. G. 2001 Virtual origin correction for lazy turbulent plumes. J. Fluid Mech. 435, 377–396.Google Scholar
Lin, T. Y.2014 Buoyancy-induced turbulent mixing in a narrow tilted tank. Master’s thesis, University of Cambridge.Google Scholar
Linden, P. F. & Simpson, J. E. 1986 Gravity-driven flows in a turbulent fluid. J. Fluid Mech. 172, 481–497.Google Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Paul, E. L., Atiemo-Obeng, V. A. & Kresta, S. M. 2004 Handbook of Industrial Mixing: Science and Practice. Wiley.Google Scholar
Séon, T., Hulin, J. P., Salin, D., Perrin, B. & Hinch, E. J. 2004 Buoyant mixing of miscible fluids in tilted tubes. Phys. Fluids 16 (12), 103–106.CrossRefGoogle Scholar
Séon, T., Hulin, J. P., Salin, D., Perrin, B. & Hinch, E. J. 2005 Buoyancy driven miscible front dynamics in tilted tubes. Phys. Fluids 17, 31702.CrossRefGoogle Scholar
Séon, T., Znaien, J., Perrin, B., Hinch, E. J., Salin, D. & Hulin, J. P. 2007 Front dynamics and macroscopic diffusion in buoyant mixing in a tilted tube. Phys. Fluids 19, 125105.Google Scholar
Simpson, J. E. & Britter, R. E. 1979 The dynamics of the head of a gravity current advancing over a horizontal surface. J. Fluid Mech. 94, 477–495.Google Scholar
Sinnott, R. K. 2005 Chemical Engineering Design: Chemical Engineering, vol. 6. Elsevier Science.Google Scholar
van Sommeren, D. D. J. A., Caulfield, C. P. & Woods, A. W. 2012 Turbulent buoyant convection from a maintained source of buoyancy in a narrow vertical tank. J. Fluid Mech. 701, 278–303; referred to herein as VS12.Google Scholar
van Sommeren, D. D. J. A., Caulfield, C. P. & Woods, A. W. 2013 Advection and buoyancy-induced turbulent mixing in a narrow vertical tank. J. Fluid Mech. 724, 450–479.Google Scholar
Taylor, G. I. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
Taylor, G. I. 1954 The dispersion of matter in turbulent flow through a pipe. Proc. R. Soc. Lond. A 223 (1155), 446–468.Google Scholar
Znaien, J., Hallez, Y., Moisy, F., Magnaudet, J., Hulin, J.-P., Salin, D. & Hinch, E. J. 2009 Experimental and numerical investigations of flow structure and momentum transport in a turbulent buoyancy-driven flow inside a tilted tube. Phys. Fluids 21 (11), 115102.Google Scholar
Znaien, J., Moisy, F. & Hulin, J. P. 2011 Flow structure and momentum transport for buoyancy driven mixing flows in long tubes at different tilt angles. Phys. Fluids 23 (3), 035105.CrossRefGoogle Scholar
Zukoski, E. E. 1995 A Review of Flows Driven by Natural Convection in Adiabatic Shafts. US Department of Commerce, Technology Administration, National Institute of Standards and Technology.Google Scholar