Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T02:20:09.645Z Has data issue: false hasContentIssue false
  • English
  • Français

Buoyancy scale effects in large-eddy simulations of stratified turbulence

Published online by Cambridge University Press:  30 July 2014

Sina Khani  and
Michael L. Waite
Sina Khani*
Affiliation:
Department of Applied Mathematics, University of Waterloo, Waterloo, Ontario, Canada N2L 3G1
Michael L. Waite
Affiliation:
Department of Applied Mathematics, University of Waterloo, Waterloo, Ontario, Canada N2L 3G1
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper large-eddy simulations (LES) of forced stratified turbulence using two common subgrid scale (SGS) models, the Kraichnan and Smagorinsky models, are studied. As found in previous studies using regular and hyper-viscosity, vorticity contours show elongated horizontal motions, which are layered in the vertical direction, along with intermittent Kelvin–Helmholtz (KH) instabilities. Increased stratification causes the layer thickness to collapse towards the dissipation scale, ultimately suppressing these instabilities. 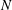The vertical energy spectra are relatively flat out to a local maximum, which varies with the buoyancy frequency $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}N$. The horizontal energy spectra depend on the grid spacing 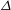$\varDelta $; if the resolution is fine enough, the horizontal spectrum shows an approximately 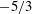$-5/3$ slope along with a bump at the buoyancy wavenumber 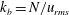$k_b = N/u_{rms}$, where 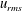$u_{rms}$ is the root-mean-square (r.m.s.) velocity. Our results show that there is a critical value of the grid spacing $\varDelta $, below which dynamics of stratified turbulence are well-captured in LES. This critical 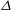$\varDelta $ depends on the buoyancy scale 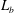$L_b$ and varies with different SGS models: the Kraichnan model requires 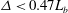$\varDelta < 0.47 L_b$, while the Smagorinsky model requires 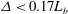$\varDelta < 0.17 L_b$. In other words, the Smagorinsky model is significantly more costly than the Kraichnan approach, as it requires three times the resolution to adequately capture stratified turbulence.

JFM classification

Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 754 , 10 September 2014 , pp. 75 - 97
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Augier, P. & Billant, P. 2011 Onest of secondary instabilities on the zigzag instability in stratified fluids. J. Fluid Mech. 682, 120–131.Google Scholar
Augier, P., Chomaz, J.-M. & Billant, P. 2012 Spectral analysis of the transition to turbulence from a dipole in stratified fluid. J. Fluid Mech. 713, 86–108.Google Scholar
Bartello, P., Métais, O. & Lesieur, M. 1996 Geostrophic versus wave eddy viscosities in atmospheric models. J. Atmos. Sci. 53, 564–571.Google Scholar
Batchelor, G. K., Canuto, V. M. & Chasnov, J. R. 1992 Homogeneous buoyancy-generated turbulence. J. Fluid Mech. 235, 349–378.CrossRefGoogle Scholar
Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13 (6), 1645–1651.Google Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.CrossRefGoogle Scholar
Brune, S. & Becker, E. 2013 Indications of stratified turbulence in a mechanistic GCM. J. Atmos. Sci. 70, 231–247.Google Scholar
Carnevale, G. F., Briscolini, M. & Orlandi, P. 2001 Buoyancy- to inertial-range transition in forced stratified turbulence. J. Fluid Mech. 427, 205–239.Google Scholar
Durran, D. R. 2010 Numerical Methods for Fluid Dynamics with Application to Geophysics. Springer.Google Scholar
Gargett, A. E., Osborn, T. R. & Nasmyth, P. W. 1984 Local isotropy and the decay of turbulence in a stratified fluid. J. Fluid Mech. 144, 231–280.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3 (7), 1760–1765.CrossRefGoogle Scholar
Hebert, D. A. & de Bruyn Kops, S. M. 2006a Relationship between vertical shear rate and kinetic energy dissipation rate in stably stratified flows. Geophys. Res. Lett. 33, L06602.Google Scholar
Hebert, D. A. & de Bruyn Kops, S. M. 2006b Predicting turbulence in flows with strong stable stratification. Phys. Fluids 18, 066602.Google Scholar
Herring, J. R. & Métais, O. 1989 Numerical experiments in forced stably stratified turbulence. J. Fluid Mech. 202, 97–115.CrossRefGoogle Scholar
Kang, H. S., Chester, S. & Meneveau, C. 2003 Decaying turbulence in an active-grid-generated flow and comparisons with large-eddy simulation. J. Fluid Mech. 480, 129–160.Google Scholar
Khani, S. & Waite, M. L. 2013 Effective eddy viscosity in stratified turbulence. J. Turbul. 14 (7), 49–70.CrossRefGoogle Scholar
Kimura, Y. & Herring, J. R. 2012 Energy spectra of stably stratified turbulence. J. Fluid Mech. 698, 19–50.Google Scholar
Kraichnan, R. H. 1976 Eddy viscosity in two and three dimensions. J. Atmos. Sci. 33, 1521–1536.Google Scholar
Laval, J.-P., McWilliams, J. C. & Dubrulle, B. 2003 Forced stratified turbulence: successive transition with Reynolds number. Phys. Rev. E 68, 036308.Google Scholar
Leonard, A. 1974 Energy cascade in large eddy simulation of turbulent fluid flow. Adv. Geophys. A 18, 237–248.Google Scholar
Lesieur, M. 1990 Turbulence in Fluids. Kluwer.Google Scholar
Lesieur, M. & Rogallo, R. 1989 Large-eddy simulation of passive scalar diffusion in isotropic turbulence. Phys. Fluids A 1 (4), 718–722.CrossRefGoogle Scholar
Lilly, D. K. 1967 The representation of small-scale turbulence in numerical simulation experiments. In NCAR Manuscript, vol. 281, pp. 99–164. National Center for Atmospheirc Research.Google Scholar
Lindborg, E. 2006 The energy cascade in strongly stratified fluid. J. Fluid Mech. 550, 207–242.CrossRefGoogle Scholar
Lumley, J. L. 1964 The spectrum of nearly inertial turbulence in stably stratified fluid. J. Atmos. Sci. 21, 99–102.Google Scholar
Meneveau, C. & Katz, J. 2000 Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 32, 1–32.Google Scholar
Moin, P., Squires, K., Cabot, W. H. & Lee, S. 1991 A dynamic subgrid-scale model for compressible turbulence and scalar transport. Phys. Fluids A 3 (11), 2746–2757.Google Scholar
Paoli, R., Thouron, O., Escobar, J., Picot, J. & Cariolle, D. 2013 High-resolution large-eddy simulations of sub-kilometer-scale turbulence in the upper troposphere lower stratoposphere. Atmos. Chem. Phys. Discuss. 13, 31891–31932.Google Scholar
Piomelli, U., Cabot, W. H., Moin, P. & Lee, S. 1991 Subgrid-scale backscatter in turbulent and transitional flows. Phys. Fluids A 3 (7), 1766–1771.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Remmler, S. & Hickel, S. 2012 Direct and large eddy simulation of stratified turbulence. Intl J. Heat Fluid Flow 35, 13–24.Google Scholar
Riley, J. J. & de Bruyn Kops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15, 2047–2059.Google Scholar
Siegel, D. A. & Domaradzki, J. A. 1994 Large-eddy simulation of decaying stably stratified turbulence. J. Phys. Oceanogr. 24, 2353–2386.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations. I. The basic experiment. Mon. Weath. Rev. 91 (3), 99–164.Google Scholar
Smith, L. M. & Waleffe, F. 2002 Generation of slow large scales in forced rotating stratified turbulence. J. Fluid Mech. 451, 145–168.Google Scholar
Waite, M. L. 2014 Direct numerical simulations of laboratory-scale stratified turbulence. In Modelling Atmospheric and Oceanic Flows: Insights from Laboratory Experiments (ed. von Larcher, T. & Williams, P.), American Geophysical Union.Google Scholar
Waite, M. L. 2011 Stratified turbulence at the buoyancy scale. Phys. Fluids A 23, 066602.Google Scholar
Waite, M. L. & Bartello, P. 2004 Stratified turbulence dominated by vortical motion. J. Fluid Mech. 517, 281–303.Google Scholar