Article contents
Buoyancy oscillations
Published online by Cambridge University Press: 03 April 2024
Abstract
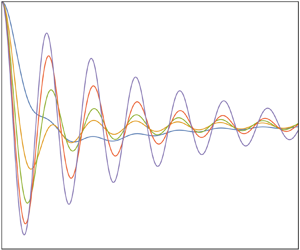
The oscillations of buoyant bodies in stratified fluids are deduced from the variations of their added mass. Three configurations are considered: a body displaced from its neutral level then released; a Cartesian diver set into oscillation by a modulation of the hydrostatic pressure, then released; and a body attached to a pendulum to which an impulse is applied. The first configuration is related to the dynamics of Lagrangian floats in the ocean. Two particular bodies are considered: an elliptic cylinder of horizontal axis, typical of two-dimensional bodies; and a spheroid of vertical axis, typical of three-dimensional bodies. The ultimate motion of the body consists of oscillations at the buoyancy frequency with an amplitude decaying algebraically with time. Before that, the resonant response of the system is observed, either aperiodic exponential decay when the system has no intrinsic dynamics, or exponentially damped oscillation otherwise. Comparison with available measurements demonstrates the need to include viscous dissipation in the analysis. At high Stokes number, dissipation comes from the Basset–Boussinesq memory force and is affected negligibly by the stratification; at low Stokes number, dissipation comes from Stokes resistance and exhibits a significant effect of the stratification.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 3
- Cited by



