Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T23:56:27.379Z Has data issue: false hasContentIssue false
  • English
  • Français

Buoyancy effects on large-scale motions in convective atmospheric boundary layers: implications for modulation of near-wall processes

Published online by Cambridge University Press:  28 September 2018

S. T. Salesky Open the ORCID record for S. T. Salesky [Opens in a new window]  and
W. Anderson Open the ORCID record for W. Anderson [Opens in a new window]
S. T. Salesky*
Affiliation:
School of Meteorology, The University of Oklahoma, Norman, OK 73072, USA
W. Anderson
Affiliation:
Mechanical Engineering Department, The University of Texas at Dallas, Richardson, TX 75080, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A number of recent studies have demonstrated the existence of so-called large- and very-large-scale motions (LSM, VLSM) that occur in the logarithmic region of inertia-dominated wall-bounded turbulent flows. These regions exhibit significant streamwise coherence, and have been shown to modulate the amplitude and frequency of small-scale inner-layer fluctuations in smooth-wall turbulent boundary layers. In contrast, the extent to which analogous modulation occurs in inertia-dominated flows subjected to convective thermal stratification (low Richardson number) and Coriolis forcing (low Rossby number), has not been considered. And yet, these parameter values encompass a wide range of important environmental flows. In this article, we present evidence of amplitude modulation (AM) phenomena in the unstably stratified (i.e. convective) atmospheric boundary layer, and link changes in AM to changes in the topology of coherent structures with increasing instability. We perform a suite of large eddy simulations spanning weakly (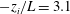$-z_{i}/L=3.1$) to highly convective (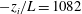$-z_{i}/L=1082$) conditions (where 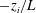$-z_{i}/L$ is the bulk stability parameter formed from the boundary-layer depth 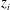$z_{i}$ and the Obukhov length 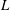$L$) to investigate how AM is affected by buoyancy. Results demonstrate that as unstable stratification increases, the inclination angle of surface layer structures (as determined from the two-point correlation of streamwise velocity) increases from 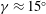$\unicode[STIX]{x1D6FE}\approx 15^{\circ }$ for weakly convective conditions to nearly vertical for highly convective conditions. As 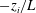$-z_{i}/L$ increases, LSMs in the streamwise velocity field transition from long, linear updrafts (or horizontal convective rolls) to open cellular patterns, analogous to turbulent Rayleigh–Bénard convection. These changes in the instantaneous velocity field are accompanied by a shift in the outer peak in the streamwise and vertical velocity spectra to smaller dimensionless wavelengths until the energy is concentrated at a single peak. The decoupling procedure proposed by Mathis et al. (J. Fluid Mech., vol. 628, 2009a, pp. 311–337) is used to investigate the extent to which amplitude modulation of small-scale turbulence occurs due to large-scale streamwise and vertical velocity fluctuations. As the spatial attributes of flow structures change from streamwise to vertically dominated, modulation by the large-scale streamwise velocity decreases monotonically. However, the modulating influence of the large-scale vertical velocity remains significant across the stability range considered. We report, finally, that amplitude modulation correlations are insensitive to the computational mesh resolution for flows forced by shear, buoyancy and Coriolis accelerations.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 856 , 10 December 2018 , pp. 135 - 168
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Agee, E. M., Chen, T. S. & Dowell, K. E. 1973 A review of mesoscale cellular convection. Bull. Am. Meteorol. Soc. 54 (10), 1004–1012.Google Scholar
Albertson, J. D. & Parlange, M. B. 1999 Surface length scales and shear stress: implications for land–atmosphere interaction over complex terrain. Water Resour. Res. 35 (7), 2121–2132.Google Scholar
Anderson, W. 2016 Amplitude modulation of streamwise velocity fluctuations in the roughness sublayer: evidence from large-eddy simulations. J. Fluid Mech. 789, 567–588.Google Scholar
Anderson, W. & Chamecki, M. 2014 Numerical study of turbulent flow over complex aeolian dune fields: the White Sands National Monument. Phys. Rev. E 89 (1), 013005.Google Scholar
Anderson, W., Li, Q. & Bou-Zeid, E. 2015 Numerical simulation of flow over urban-like topographies and evaluation of turbulence temporal attributes. J. Turbul. 16 (9), 809–831.Google Scholar
Anderson, W. & Meneveau, C. 2011 Dynamic roughness model for large-eddy simulation of turbulent flow over multiscale, fractal-like rough surfaces. J. Fluid Mech. 679, 288–314.Google Scholar
Atkinson, B. W. & Zhang, J. 1996 Mesoscale shallow convection in the atmosphere. Rev. Geophys. 34 (4), 403–431.Google Scholar
Awasthi, A. & Anderson, W. 2018 Numerical study of turbulent channel flow perturbed by spanwise topographic heterogeneity: amplitude and frequency modulation within low–and high-momentum pathways. Phys. Rev. Fluids 3, 044602.Google Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2016 Spectral stochastic estimation of high-Reynolds-number wall-bounded turbulence for a refined inner–outer interaction model. Phys. Rev. Fluids 1, 054406.Google Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2017 Reynolds number trend of hierarchies and scale interactions in turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 375 (2089), 20160077.Google Scholar
Baars, W. J., Talluru, K. M., Hutchins, N. & Marusic, I. 2015 Wavelet analysis of wall turbulence to study large-scale modulation of small scales. Exp. Fluids 56 (10), 188.Google Scholar
Bailey, B. N. & Stoll, R. 2013 Turbulence in sparse, organized vegetative canopies: a large-eddy simulation study. Boundary-Layer Meteorol. 147 (3), 369–400.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large-and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365 (1852), 665–681.Google Scholar
Baldocchi, D. D., Hincks, B. B. & Meyers, T. P. 1988 Measuring biosphere–atmosphere exchanges of biologically related gases with micrometeorological methods. Ecology 69 (5), 1331–1340.Google Scholar
Bandyopadhyay, P. R. & Hussain, A. K. M. F. 1984 The coupling between scales in shear flows. Phys. Fluids 27 (9), 2221–2228.Google Scholar
Banerjee, T. & Katul, G. G. 2013 Logarithmic scaling in the longitudinal velocity variance explained by a spectral budget. Phys. Fluids 25 (12), 125106.Google Scholar
Banerjee, T., Katul, G. G., Salesky, S. T. & Chamecki, M. 2015 Revisiting the formulations for the longitudinal velocity variance in the unstable atmospheric surface layer. Q. J. R. Meteorol. Soc. 141 (690), 1699–1711.Google Scholar
Bendat, J. S. & Piersol, A. G. 2010 Random Data Analysis and Measurement Procedures. Wiley.Google Scholar
Boppe, R. S. & Neu, W. L. 1995 Quasi-coherent structures in the marine atmospheric surface layer. J. Geophys. Res. 100 (C10), 20635–20648.Google Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. B. 2005 A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 17 (2), 025105.Google Scholar
Brown, G. L. & Thomas, A. S. W. 1977 Large structure in a turbulent boundary layer. Phys. Fluids 20 (10), S243–S252.Google Scholar
Brown, R. A. 1980 Longitudinal instabilities and secondary flows in the planetary boundary layer: a review. Rev. Geophys. 18 (3), 683–697.Google Scholar
Brutsaert, W. & Stricker, H. 1979 An advection-aridity approach to estimate actual regional evapotranspiration. Water Resour. Res. 15 (2), 443–450.Google Scholar
Businger, J. A., Wyngaard, J. C., Izumi, Y. & Bradley, E. F. 1971 Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 28 (2), 181–189.Google Scholar
Calaf, M., Meneveau, C. & Meyers, J. 2010 Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 22 (1), 015110.Google Scholar
Calaf, M., Parlange, M. B. & Meneveau, C. 2011 Large eddy simulation study of scalar transport in fully developed wind-turbine array boundary layers. Phys. Fluids 23 (12), 126603.Google Scholar
Cantwell, B. J. 1981 Organized motion in turbulent flow. Annu. Rev. Fluid Mech. 13 (1), 457–515.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Thomas, A. Jr. 2012 Spectral Methods in Fluid Dynamics. Springer Science and Business Media.Google Scholar
Carper, M. A. & Porté-Agel, F. 2004 The role of coherent structures in subfilter-scale dissipation of turbulence measured in the atmospheric surface layer. J. Turbul. 5, 040.Google Scholar
Chamecki, M., Dias, N. L., Salesky, S. T. & Pan, Y. 2017 Scaling laws for the longitudinal structure function in the atmospheric surface layer. J. Atmos. Sci. 74 (4), 1127–1147.Google Scholar
Chamecki, M., Meneveau, C. & Parlange, M. B. 2009 Large eddy simulation of pollen transport in the atmospheric boundary layer. J. Aerosol Sci. 40 (3), 241–255.Google Scholar
Chauhan, K., Hutchins, N., Monty, J. & Marusic, I. 2013 Structure inclination angles in the convective atmospheric surface layer. Boundary-Layer Meteorol. 147 (1), 41–50.Google Scholar
Cheng, H. & Castro, I. P. 2002 Near wall flow over urban-like roughness. Boundary-Layer Meteorol. 104 (2), 229–259.Google Scholar
Chester, S., Meneveau, C. & Parlange, M. B. 2007 Modeling turbulent flow over fractal trees with renormalized numerical simulation. J. Comput. Phys. 225 (1), 427–448.Google Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.Google Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.Google Scholar
Cline, D. W. 1997 Snow surface energy exchanges and snowmelt at a continental, midlatitude alpine site. Water Resour. Res. 33 (4), 689–701.Google Scholar
Coceal, O., Dobre, A., Thomas, T. G. & Belcher, S. E. 2007 Structure of turbulent flow over regular arrays of cubical roughness. J. Fluid Mech. 589, 375–409.Google Scholar
Conzemius, R. J. & Fedorovich, E. 2006 Dynamics of sheared convective boundary layer entrainment. Part I: methodological background and large-eddy simulations. J. Atmos. Sci. 63 (4), 1151–1178.Google Scholar
Corino, E. R. & Brodkey, R. S. 1969 A visual investigation of the wall region in turbulent flow. J. Fluid Mech. 37 (1), 1–30.Google Scholar
Deardorff, J. W. 1972a Numerical investigation of neutral and unstable planetary boundary layers. J. Atmos. Sci. 29 (1), 91–115.Google Scholar
Deardorff, J. W. 1972b Parameterization of the planetary boundary layer for use in general circulation models. Mon. Weath. Rev. 100 (2), 93–106.Google Scholar
Del Alamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011a Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011b Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.Google Scholar
Dosio, A., Vilà-Guerau de Arellano, J., Holtslag, A. A. M. & Builtjes, P. J. H. 2003 Dispersion of a passive tracer in buoyancy- and shear-driven boundary layers. J. Appl. Meteorol. 42 (8), 1116–1130.Google Scholar
Fang, J. & Porté-Agel, F. 2015 Large-eddy simulation of very-large-scale motions in the neutrally stratified atmospheric boundary layer. Boundary-Layer Meteorol. 155 (3), 397–416.Google Scholar
Finnigan, J. J., Shaw, R. H. & Patton, E. G. 2009 Turbulence structure above a vegetation canopy. J. Fluid Mech. 637, 387–424.Google Scholar
Flack, K. A., Schultz, M. P. & Shapiro, T. A. 2005 Experimental support for Townsend’s Reynolds number similarity hypothesis on rough walls. Phys. Fluids 17 (3), 035102.Google Scholar
Frenzen, P. & Vogel, C. A. 1992 The turbulent kinetic energy budget in the atmospheric surface layer: a review and an experimental reexamination in the field. Boundary-Layer Meteorol. 60 (1), 49–76.Google Scholar
Frenzen, P. & Vogel, C. A. 2001 Further studies of atmospheric turbulence in layers near the surface: scaling the TKE budget above the roughness sublayer. Boundary-Layer Meteorol. 99 (2), 173–206.Google Scholar
Ganapathisubramani, B., Hutchins, N., Hambleton, W. T., Longmire, E. K. & Marusic, I. 2005 Investigation of large-scale coherence in a turbulent boundary layer using two-point correlations. J. Fluid Mech. 524, 57–80.Google Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3, 1760.Google Scholar
Giometto, M. G., Christen, A., Egli, P. E., Schmid, M. F., Tooke, R. T., Coops, N. C. & Parlange, M. B. 2017 Effects of trees on mean wind, turbulence and momentum exchange within and above a real urban environment. Adv. Water Resour. 106, 154–168.Google Scholar
Giometto, M. G., Christen, A., Meneveau, C., Fang, J., Krafczyk, M. & Parlange, M. B. 2016 Spatial characteristics of roughness sublayer mean flow and turbulence over a realistic urban surface. Boundary-Layer Meteorol. 160 (3), 425–452.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
Guala, M. M. M. & McKeon, B. J. 2011 Interactions within the turbulent boundary layer at high Reynolds number. J. Fluid Mech. 666, 573–604.Google Scholar
Hambleton, W. T., Hutchins, N. & Marusic, I. 2006 Simultaneous orthogonal-plane particle image velocimetry measurements in a turbulent boundary layer. J. Fluid Mech. 560, 53–64.Google Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.Google Scholar
Hellström, L. H. O., Ganapathisubramania, B. & Smits, A. J. 2015 The evolution of large-scale motions in turbulent pipe flow. J. Fluid Mech. 779, 701–715.Google Scholar
Högström, U. L. F. 1988 Non-dimensional wind and temperature profiles in the atmospheric surface layer: a re-evaluation. Boundary-Layer Meteorol. 42 (1), 55–78.Google Scholar
Hommema, S. E. & Adrian, R. J. 2003 Packet structure of surface eddies in the atmospheric boundary layer. Boundary-Layer Meteorol. 106 (1), 147–170.Google Scholar
Hristov, T., Friehe, C. & Miller, S. 1998 Wave-coherent fields in air flow over ocean waves: identification of cooperative behavior buried in turbulence. Phys. Rev. Lett. 81 (23), 5245.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108 (9), 094501.Google Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145 (2), 273–306.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Jacob, C. & Anderson, W. 2017 Conditionally averaged large-scale motions in the neutral atmospheric boundary layer: insights for aeolian processes. Boundary-Layer Meteorol. 162 (1), 21–41.Google Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Jiménez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, P1.Google Scholar
Johansson, C., Smedman, A. S., Högström, U., Brasseur, J. G. & Khanna, S. 2001 Critical test of the validity of Monin–Obukhov similarity during convective conditions. J. Atmos. Sci. 58 (12), 1549–1566.Google Scholar
Kaimal, J. C. & Finnigan, J. J. 1994 Atmospheric Boundary Layer Flows: Their Structure and Measurement. Oxford University Press.Google Scholar
Kaimal, J. C., Wyngaard, J. C., Izumi, Y. & Coté, O. R. 1972 Spectral characteristics of surface-layer turbulence. Q. J. R. Meteorol. Soc. 98 (417), 563–589.Google Scholar
Kang, H. S. & Meneveau, C. 2002 Universality of large eddy simulation model parameters across a turbulent wake behind a heated cylinder. J. Turbul. 3, N26.Google Scholar
Khanna, S. & Brasseur, J. G. 1997 Analysis of Monin–Obukhov similarity from large-eddy simulation. J. Fluid Mech. 345, 251–286.Google Scholar
Khanna, S. & Brasseur, J. G. 1998 Three-dimensional buoyancy-and shear-induced local structure of the atmospheric boundary layer. J. Atmos. Sci. 55 (5), 710–743.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Kleissl, J., Kumar, V., Meneveau, C. & Parlange, M. B. 2006 Numerical study of dynamic Smagorinsky models in large-eddy simulation of the atmospheric boundary layer: validation in stable and unstable conditions. Water Resour. Res. 42, W06D10.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30 (04), 741–773.Google Scholar
Kovasznay, L. S. G., Kibens, V. & Blackwelder, R. F. 1970 Large-scale motion in the intermittent region of a turbulent boundary layer. J. Fluid Mech. 41 (02), 283–325.Google Scholar
Kumar, V., Kleissl, J., Meneveau, C. & Parlange, M. B. 2006 Large-eddy simulation of a diurnal cycle of the atmospheric boundary layer: atmospheric stability and scaling issues. Water Resour. Res. 42 (6), W06D09.Google Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high-Reynolds-number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.Google Scholar
Lee, J. H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.Google Scholar
LeMone, M. A. 1973 The structure and dynamics of horizontal roll vortices in the planetary boundary layer. J. Atmos. Sci. 30 (6), 1077–1091.Google Scholar
LeMone, M. A. 1976 Modulation of turbulence energy by longitudinal rolls in an unstable planetary boundary layer. J. Atmos. Sci. 33 (7), 1308–1320.Google Scholar
Louis, J. F. 1979 A parametric model of vertical eddy fluxes in the atmosphere. Boundary-Layer Meteorol. 17 (2), 187–202.Google Scholar
Marusic, I. & Heuer, W. D. C. 2007 Reynolds number invariance of the structure inclination angle in wall turbulence. Phys. Rev. Lett. 99 (11), 114504.Google Scholar
Marusic, I. & Hutchins, N. 2008 Study of the log-layer structure in wall turbulence over a very large range of Reynolds number. Flow Turbul. Combust. 81 (1–2), 115–130.Google Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15 (8), 2461–2464.Google Scholar
Marusic, I., Kunkel, G. J. & Porté-Agel, F. 2001 Experimental study of wall boundary conditions for large-eddy simulation. J. Fluid Mech. 446, 309–320.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010a Predictive model for wall-bounded turbulent flow. Science 329 (5988), 193–196.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010b Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22 (6), 065103.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009a Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.Google Scholar
Mathis, R., Monty, J. P., Hutchins, N. & Marusic, I. 2009b Comparison of large-scale amplitude modulation in turbulent boundary layers, pipes, and channel flows. Phys. Fluids 21 (11), 111703.Google Scholar
McLean, I. R.1990 The near wall eddy structure in an equilibrium turbulent boundary layer. PhD thesis, University of Southern California.Google Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7 (4), 694–696.Google Scholar
Meneveau, C., Lund, T. S. & Cabot, W. H. 1996 A Lagrangian dynamic subgrid-scale model of turbulence. J. Fluid Mech. 319, 353–385.Google Scholar
Meneveau, C. & Marusic, I. 2013 Generalized logarithmic law for high-order moments in turbulent boundary layers. J. Fluid Mech. 719, R1.Google Scholar
Moeng, C. H. 1984 A large-eddy-simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 41 (13), 2052–2062.Google Scholar
Moeng, C. H. & Sullivan, P. P. 1994 A comparison of shear-and buoyancy-driven planetary boundary layer flows. J. Atmos. Sci. 51 (7), 999–1022.Google Scholar
Moncrieff, J., Valentini, R., Greco, S., Guenther, S. & Ciccioli, P. 1997 Trace gas exchange over terrestrial ecosystems: methods and perspectives in micrometeorology. J. Expl Bot. 48 (5), 1133–1142.Google Scholar
Monin, A. S. & Obukhov, A. M. 1954 Turbulent mixing in the atmospheric surface layer. Tr. Akad. Nauk SSSR Geofiz. Inst. 24 (151), 163–187.Google Scholar
Morris, S. C., Stolpa, S. R., Slaboch, P. E. & Klewicki, J. C. 2007 Near-surface particle image velocimetry measurements in a transitionally rough-wall atmospheric boundary layer. J. Fluid Mech. 580, 319–338.Google Scholar
Murlis, J., Tsai, H. M. & Bradshaw, P. 1982 The structure of turbulent boundary layers at low Reynolds numbers. J. Fluid Mech. 122, 13–56.Google Scholar
Nakagawa, H. & Nezu, I. 1981 Structure of space-time correlations of bursting phenomena in an open-channel flow. J. Fluid Mech. 104, 1–43.Google Scholar
Nieuwstadt, F. T. M., Mason, P. J., Moeng, C.-H. & Schumann, U. 1993 Large-eddy simulation of the convective boundary layer: a comparison of four computer codes. In Turbulent Shear Flows, vol. 8, pp. 343–367. Springer.Google Scholar
Obukhov, A. M. 1946 Turbulence in an atmosphere with temperature inhomogeneities. Tr. Inst. Theor. Geofiz 1, 95–115.Google Scholar
Panofsky, H. A., Tennekes, H., Lenschow, D. H. & Wyngaard, J. C. 1977 The characteristics of turbulent velocity components in the surface layer under convective conditions. Boundary-Layer Meteorol. 11 (3), 355–361.Google Scholar
Panton, R. L. 2001 Overview of the self-sustaining mechanisms of wall turbulence. Prog. Aerosp. Sci. 37 (4), 341–383.Google Scholar
Parlange, M. B., Eichinger, W. E. & Albertson, J. D. 1995 Regional scale evaporation and the atmospheric boundary layer. Rev. Geophys. 33 (1), 99–124.Google Scholar
Pathikonda, G. & Christensen, K. T. 2017 Inner–outer interactions in a turbulent boundary layer overlying complex roughness. Phys. Rev. Fluids 2 (4), 044603.Google Scholar
Penman, H. L. 1948 Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. A 193, 120–145.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Philips, D. A., Rossi, R. & Iaccarino, G. 2013 Large-eddy simulation of passive scalar dispersion in an urban-like canopy. J. Fluid Mech. 723, 404–428.Google Scholar
Piomelli, U. & Balaras, E. 2002 Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 34 (1), 349–374.Google Scholar
Piomelli, U., Ferziger, J., Moin, P. & Kim, J. 1989 New approximate boundary conditions for large eddy simulations of wall-bounded flows. Phys. Fluids A 1 (6), 1061–1068.Google Scholar
Pope, S. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rajagopalan, S. & Antonia, R. A. 1979 Some properties of the large structure in a fully developed turbulent duct flow. Phys. Fluids 22 (4), 614–622.Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44 (1), 1–25.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.Google Scholar
Salesky, S. T. & Chamecki, M. 2012 Random errors in turbulence measurements in the atmospheric surface layer: implications for Monin–Obukhov similarity theory. J. Atmos. Sci. 69 (12), 3700–3714.Google Scholar
Salesky, S. T., Chamecki, M. & Bou-Zeid, E. 2017 On the nature of the transition between roll and cellular organization in the convective boundary layer. Boundary-Layer Meteorol. 163 (1), 1–28.Google Scholar
Salesky, S. T., Katul, G. G. & Chamecki, M. 2013 Buoyancy effects on the integral lengthscales and mean velocity profile in atmospheric surface layer flows. Phys. Fluids 25 (10), 105101.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Squire, D. T., Baars, W. J., Hutchins, N. & Marusic, I. 2016 Inner–outer interactions in rough-wall turbulence. J. Turbul. 17 (12), 1159–1178.Google Scholar
Sreenivasan, K. R. 1985 On the fine-scale intermittency of turbulence. J. Fluid Mech. 151, 81–103.Google Scholar
Sullivan, P. P., Horst, T. W., Lenschow, D. H., Moeng, C. H. & Weil, J. C. 2003 Structure of subfilter-scale fluxes in the atmospheric surface layer with application to large-eddy simulation modelling. J. Fluid Mech. 482 (1), 101–139.Google Scholar
Sullivan, P. P. & Patton, E. G. 2011 The effect of mesh resolution on convective boundary layer statistics and structures generated by large-eddy simulation. J. Atmos. Sci. 68 (10), 2395–2415.Google Scholar
Sykes, R. I. & Henn, D. S. 1989 Large-eddy simulation of turbulent sheared convection. J. Atmos. Sci. 46 (8), 1106–1118.Google Scholar
Tardu, S. F. 2008 Stochastic synchronization of the near wall turbulence. Phys. Fluids 20 (4), 045105.Google Scholar
Theodorsen, T. 1952 Mechanism of turbulence. In Proceedings of the Second Midwestern Conference on Fluid Mechanics, vol. 1719. Ohio State University.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2007 Turbulence structure in rough-and smooth-wall boundary layers. J. Fluid Mech. 592, 263–293.Google Scholar
Wallace, J. M. 2016 Quadrant analysis in turbulence research: history and evolution. Annu. Rev. Fluid Mech. 48, 131–158.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54 (01), 39–48.Google Scholar
Wark, C. E. & Nagib, H. M. 1991 Experimental investigation of coherent structures in turbulent boundary layers. J. Fluid Mech. 230, 183–208.Google Scholar
Weckwerth, T. M., Horst, T. W. & Wilson, J. W. 1999 An observational study of the evolution of horizontal convective rolls. Mon. Weath. Rev. 127 (9), 2160–2179.Google Scholar
Weckwerth, T. M., Wilson, J. W. & Wakimoto, R. M. 1996 Thermodynamic variability within the convective boundary layer due to horizontal convective rolls. Mon. Weath. Rev. 124 (5), 769–784.Google Scholar
Weckwerth, T. M., Wilson, J. W., Wakimoto, R. M. & Crook, N. A. 1997 Horizontal convective rolls: determining the environmental conditions supporting their existence and characteristics. Mon. Weath. Rev. 125 (4), 505–526.Google Scholar
Wilczek, M., Stevens, R. J. A. M. & Meneveau, C. 2015 Spatio-temporal spectra in the logarithmic layer of wall turbulence: large-eddy simulations and simple models. J. Fluid. Mech 769, R1.Google Scholar
Willmarth, W. W. & Lu, S. S. 1972 Structure of the Reynolds stress near the wall. J. Fluid Mech. 55 (01), 65–92.Google Scholar
Wu, X., Baltzer, J. R. & Adrian, R. J. 2012 Direct numerical simulation of a 30R long turbulent pipe flow at R + = 685: large-and very large-scale motions. J. Fluid Mech. 698, 235–281.Google Scholar
Wu, Y. & Christensen, K. T. 2007 Outer-layer similarity in the presence of a practical rough-wall topology. Phys. Fluids 19, 085108.Google Scholar
Wu, Y. & Christensen, K. T. 2010 Spatial structure of a turbulent boundary layer with irregular surface roughness. J. Fluid Mech. 655, 380–418.Google Scholar
Wyngaard, J. C. & Coté, O. R. 1971 The budgets of turbulent kinetic energy and temperature variance in the atmospheric surface layer. J. Atmos. Sci. 28 (2), 190–201.Google Scholar
Young, G. S., Kristovich, D. A. R., Hjelmfelt, M. R. & Foster, R. C. 2002 Rolls, streets, waves, and more: a review of quasi-two-dimensional structures in the atmospheric boundary layer. Bull. Am. Meteorol. Soc. 83 (7), 997–1001.Google Scholar