Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T22:51:23.322Z Has data issue: false hasContentIssue false
  • English
  • Français

Budgets of turbulent kinetic energy, Reynolds stresses, variance of temperature fluctuations and turbulent heat fluxes in a round jet

Published online by Cambridge University Press:  05 June 2015

Alexis Darisse ,
Jean Lemay Open the ORCID record for Jean Lemay [Opens in a new window]  and
Azemi Benaïssa
Alexis Darisse
Affiliation:
Department of Mechanical Engineering, Université Laval, 1065 avenue de la Médecine, Québec City, QC, G1V 0A6, Canada
Jean Lemay*
Affiliation:
Department of Mechanical Engineering, Université Laval, 1065 avenue de la Médecine, Québec City, QC, G1V 0A6, Canada
Azemi Benaïssa
Affiliation:
Department of Mechanical and Aerospace Engineering, Royal Military College of Canada, PO Box 17000, Station Forces, Kingston, ON, K7K 7B4, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The self-preserving region of a free round turbulent air jet at high Reynolds number is investigated experimentally (at 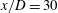$x/D=30$, 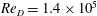$\mathit{Re}_{D}=1.4\times 10^{5}$ and 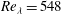$\mathit{Re}_{{\it\lambda}}=548$). Air is slightly heated ($20\,^{\circ }\text{C}$ above ambient) in order to use temperature as a passive scalar. Laser doppler velocimetry and simultaneous laser doppler velocimetry–cold-wire thermometry measurements are used to evaluate turbulent kinetic energy and temperature variance budgets in identical flow conditions. Special attention is paid to the control of initial conditions and the statistical convergence of the data acquired. Measurements of the variance, third-order moments and mixed correlations of velocity and temperature are provided (including 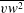$\overline{vw^{2}}$, 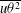$\overline{u{\it\theta}^{2}}$, 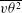$\overline{v{\it\theta}^{2}}$, 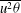$\overline{u^{2}{\it\theta}}$, 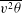$\overline{v^{2}{\it\theta}}$ and 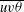$\overline{uv{\it\theta}}$). The agreement of the present results with the analytical expressions given by the continuity, mean momentum and mean enthalpy equations supports their consistency. The turbulent kinetic energy transport budget is established using Lumley’s model for the pressure diffusion term. Dissipation is inferred as the closing balance. The transport budgets of the 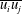$\overline{u_{i}u_{j}}$ components are also determined, which enables analysis of the turbulent kinetic energy redistribution mechanisms. The impact of the surrogacy 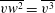$\overline{vw^{2}}=\overline{v^{3}}$ is then analysed in detail. In addition, the present data offer an opportunity to evaluate every single term of the passive scalar transport budget, except for the dissipation, which is also inferred as the closing balance. Hence, estimates of the dissipation rates of turbulent kinetic energy and temperature fluctuations (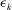${\it\epsilon}_{k}$ and ${\it\epsilon}_{{\it\theta}}$) are proposed here for use in future studies of the passive scalar in a turbulent round jet. Finally, the budgets of turbulent heat fluxes (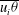$\overline{u_{i}{\it\theta}}$) are presented.

JFM classification

Wakes/Jets: Jets Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 774 , 10 July 2015 , pp. 95 - 142
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A. & Browne, L. W. B. 1983 The destruction of temperature fluctuations in a turbulent plane jet. J. Fluid Mech. 134, 67–83.CrossRefGoogle Scholar
Antonia, R. A., Browne, L. W. B., Chambers, A. J. & Rajagopalan, S. 1983 Budget of the temperature variance in a turbulent plane jet. Intl J. Heat Mass Transfer 26 (1), 41–48.CrossRefGoogle Scholar
Antonia, R. A., Chambers, A. J. & Hussain, A. K. M. F. 1980 Errors in simultaneous measurements of temperature and velocity in the outer part of a heated jet. Phys. Fluids 23 (5), 871–874.CrossRefGoogle Scholar
Antonia, R. A. & Mi, J. 1993 Temperature dissipation in a turbulent round jet. J. Fluid Mech. 250, 531–551.CrossRefGoogle Scholar
Antonia, R. A., Prabhu, A. & Stephenson, S. E. 1975 Conditionally sampled measurements in a heated turbulent jet. J. Fluid Mech. 72 (3), 455–480.CrossRefGoogle Scholar
Babu, P. & Mahesh, K.2005 Direct numerical simulation of passive scalar mixing in spatially evolving turbulent round jets. In 43rd AIAA Aerospace Sciences Meeting and Exhibit (10–13 January 2005, Reno, NV), paper no. 1121. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Benedict, L. H. & Gould, R. D. 1996 Towards better uncertainty estimates for turbulence statistics. Exp. Fluids 22 (2), 129–136.CrossRefGoogle Scholar
Bogey, C. & Bailly, C. 2009 Turbulence and energy budget in a self-preserving round jet: direct evaluation using large eddy simulation. J. Fluid Mech. 627, 129–160.CrossRefGoogle Scholar
Browne, L., Antonia, R. A. & Chua, L. P. 1989 Velocity vector cone angle in turbulent flows. Exp. Fluids 8, 13–16.CrossRefGoogle Scholar
Buchhave, P., George, W. K. & Lumley, J. L. 1979 The measurement of turbulence with the laser-Doppler anemometer. Annu. Rev. Fluid Mech. 11, 443–503.CrossRefGoogle Scholar
Chevray, R. & Tutu, N. K. 1972 Simultaneous measurements of temperature and velocity in heated flows. Rev. Sci. Instrum. 43 (10), 1417–1421.CrossRefGoogle Scholar
Chevray, R. & Tutu, N. K. 1978 Intermittency and preferential transport of heat in a round jet. J. Fluid Mech. 88 (1), 133–160.CrossRefGoogle Scholar
Chua, L. P. & Antonia, R. A. 1986 The turbulent interaction region of a circular jet. Intl Commun. Heat Mass Transfer 13 (5), 545–558.CrossRefGoogle Scholar
Chua, L. P. & Antonia, R. A. 1990 Turbulent Prandtl number in a circular jet. Intl J. Heat Mass Transfer 33 (2), 331–339.CrossRefGoogle Scholar
Coleman, H. W. & Steele, W. G. 1999 Experimentation and Uncertainty Analysis for Engineers. Wiley.Google Scholar
Combest, D. P., Ramachandran, P. A. & Dudukovic, M. P. 2011 On the gradient diffusion hypothesis and passive scalar transport in turbulent flows. Ind. Engng Chem. Res. 50 (15), 8817–8823.CrossRefGoogle Scholar
Corrsin, S. & Uberoi, M. S.1950 Further investigations on the flow and heat transfer in a heated turbulent air jet. Tech. Rep. NACA 998. National Advisory Committee for Aeronautics, UK.Google Scholar
Darisse, A., Lemay, J. & Benaïssa, A. 2013a Investigation of passive scalar mixing in a turbulent free jet using simultaneous LDV and cold wire measurements. Intl J. Heat Fluid Flow 44, 284–292.CrossRefGoogle Scholar
Darisse, A., Lemay, J. & Benaïssa, A. 2013b LDV measurements of well converged third order moments in the far field of a free turbulent round jet. Exp. Therm. Fluid Sci. 44, 825–833.CrossRefGoogle Scholar
Darisse, A., Lemay, J. & Benaïssa, A. 2014 Extensive study of temperature dissipation measurements on the centerline of a turbulent round jet based on the $\overline{{\it\theta}^{2}}/2$ budget. Exp. Fluids 55 (1), 1–15.CrossRefGoogle Scholar
Edwards, R. V., Dybbs, A., Adrian, R., Boutier, A., Eaton, J., George, W. & Meyers, J. 1987 Report of the Special Panel on statistical particle bias problems in laser anemometry. Trans. ASME J. Fluids Engng 109, 89–93.CrossRefGoogle Scholar
Friehe, C. A., Van Atta, C. W. & Gibson, C. H.1972 Jet turbulence dissipation rate measurements and correlations. In Turbulent Shear Flows, AGARD Conference Proceedings, vol. 93, pp. 298–304. NATO Advisory Group for Aerospace Research and Development.Google Scholar
George, W. K. 1990 Governing equations, experiments, and the experimentalist. Exp. Therm. Fluid Sci. 3 (6), 557–566.CrossRefGoogle Scholar
George, W. K., Beuther, P. D. & Lumley, J. L. 1978 Processing of random signals. In Proceedings of the Dynamic Flow Conference 1978 on Dynamic Measurements in Unsteady Flows, pp. 757–800. Springer.CrossRefGoogle Scholar
George, W. K. & Hussein, H. J. 1991 Locally axisymmetric turbulence. J. Fluid Mech. 233, 1–23.CrossRefGoogle Scholar
Gouldin, F. C., Schefer, R. W., Johnson, S. C. & Kollmann, W. 1986 Nonreacting turbulent mixing flows. Prog. Energy Combust. Sci. 12 (4), 257–303.CrossRefGoogle Scholar
Heist, D. K. & Castro, I. P. 1998 Combined laser-doppler and cold wire anemometry for turbulent heat flux measurement. Exp. Fluids 24, 375–381.CrossRefGoogle Scholar
Herrin, J. L. & Dutton, J. C. 1993 An investigation of LDV velocity bias correction techniques for high-speed separated flows. Exp. Fluids 15, 354–363.CrossRefGoogle Scholar
Heskestad, G. 1965 Hot-wire measurements in a plane turbulent jet. Trans. ASME J. Appl. Mech. 32 (4), 721–734.CrossRefGoogle Scholar
Hussein, H. J., Capp, S. P. & George, W. K. 1994 Velocity measurements in a high-Reynolds-number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 258, 31–75.CrossRefGoogle Scholar
Hussein, H. J. & George, W. K.1989 Measurement of small scale turbulence in an axisymmetric jet using moving hot-wires. In 7th Symposium on Turbulent Shear Flows (August 21–23, Stanford), vol. 2, paper no. 30. Pennsylvania State University.Google Scholar
Iyer, V. A. & Woodmansee, M. A. 2005 Uncertainty analysis of laser-doppler-velocimetry measurements fin a swirling flowfield. AIAA J. 43 (3), 512–519.CrossRefGoogle Scholar
Khorsandi, B., Gaskin, S. & Mydlarski, L. 2013 Effect of background turbulence on an axisymmetric turbulent jet. J. Fluid Mech. 736, 250–286.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Fluid Mechanics, Course of Theoretical Physics, vol. 6. Elsevier.Google Scholar
Launder, B. E. 1975 On the effects of a gravitational field on the turbulent transport of heat and momentum. J. Fluid Mech. 67, 569–581.CrossRefGoogle Scholar
Lemay, J. & Benaïssa, A. 2001 Improvement of cold-wire response for measurement of temperature dissipation. Exp. Fluids 31, 347–356.CrossRefGoogle Scholar
Lipari, G. & Stansby, P. 2011 Review of experimental data on incompressible turbulent round jets. Flow Turbul. Combust. 87, 79–114.CrossRefGoogle Scholar
Lumley, J. L. 1978 Computational modeling of turbulent flows. Adv. Appl. Mech. 18, 123–176.CrossRefGoogle Scholar
Malmström, T. G., Kirkpatrick, A. T., Christensen, B. & Knappmiller, K. D. 1997 Centreline velocity decay measurements in low-velocity axisymmetric jets. J. Fluid Mech. 346, 363–377.CrossRefGoogle Scholar
McLaughlin, D. K. & Tiederman, W. G. 1973 Biasing correction for individual realization of laser anemometer measurements in turbulent flows. Phys. Fluids 16 (12), 2082–2088.CrossRefGoogle Scholar
Mi, J., Nobes, D. S. & Nathan, G. J. 2001 Influence of jet exit conditions on the passive scalar field of an axisymmetric free jet. J. Fluid Mech. 432, 91–125.CrossRefGoogle Scholar
Panchapakesan, N. R. & Lumley, J. L. 1993a Turbulence measurements in axisymmetric jets of air and helium. Part 1. Air jet. J. Fluid Mech. 246, 197–223.CrossRefGoogle Scholar
Panchapakesan, N. R. & Lumley, J. L. 1993b Turbulence measurements in axisymmetric jets of air and helium. Part 2. Helium jet. J. Fluid Mech. 246, 225–247.CrossRefGoogle Scholar
Pietri, L.1997 Étude expérimentale de jets turbulents axisymétriques a densité variable. Analyse des propriétés statistiques des échelles du champ dynamique. PhD thesis, Université de la Méditerranée, Insitut de recherche sur les phénomènes hors-équilibre.Google Scholar
Pietri, L., Amielh, M. & Anselmet, F. 2000 Simultaneous measurements of temperature and velocity fluctuations in a slightly heated jet combining a cold wire and Laser Doppler Anemometry. Intl J. Heat Fluid Flow 21 (1), 22–36.CrossRefGoogle Scholar
Ruffin, E., Schiestel, R., Anselmet, F., Amielh, M. & Fulachier, L. 1994 Investigation of characteristic scales in variable density turbulent jets using a second-order model. Phys. Fluids 6 (8), 2785–2799.CrossRefGoogle Scholar
Stevenson, W. H. & Thompson, H. D. 1982 Direct measurement of laser velocimeter bias errors in a turbulent flow. AIAA J. 20, 1720–1723.CrossRefGoogle Scholar
Taub, G. N., Lee, H., Balachandar, S. & Sherif, S. A. 2013 A direct numerical simulation study of higher order statistics in a turbulent round jet. Phys. Fluids 25 (11), 115102.CrossRefGoogle Scholar
Terashima, O., Sakai, Y. & Nagata, K. 2012 Simultaneous measurement of velocity and pressure in a plane jet. Exp. Fluids 53 (4), 1149–1164.CrossRefGoogle Scholar
Thiesset, F., Antonia, R. A. & Djenidi, L. 2014 Consequences of self-preservation on the axis of a turbulent round jet. J. Fluid Mech. 748, R2.CrossRefGoogle Scholar
Tholet, K. A. & Bogart, D. G. 1994 Simultaneous temperature and velocity measurements. Meas. Sci. Technol. 5, 435–439.CrossRefGoogle Scholar
Townsend, A. A. 1949 The fully developed wake of a circular cylinder. Austral. J. Sci. Res. A 2, 451–468.Google Scholar
Wang, Z., He, P., Lv, Y., Zhou, J., Fan, J. & Cen, K. 2010 Direct numerical simulation of subsonic round turbulent jet. Flow Turbul. Combust. 84 (4), 669–686.CrossRefGoogle Scholar
Wardana, I., Ueda, T. & Mizomoto, M. 1995 Velocity–temperature correlation in strongly heated channel flow. Exp. Fluids 18, 454–461.CrossRefGoogle Scholar
Weiss, F., Paranthoën, P. & Lecordier, J.-C. 2005 Frequency response of a cold-wire in a flow seeded with oil particles. Exp. Fluids 39 (5), 935–940.CrossRefGoogle Scholar
Wygnanski, I. & Fiedler, H. 1969 Some measurements in the self-preserving jet. J. Fluid Mech. 38 (3), 577–612.CrossRefGoogle Scholar
Xu, G. & Antonia, R. 2002 Effect of different initial conditions on a turbulent round free jet. Exp. Fluids 33 (5), 677–683.CrossRefGoogle Scholar
Zhang, Z. 2002 Velocity bias in LDA measurements and its dependence on the flow turbulence. Flow Meas. Instrum. 13 (3), 63–68.CrossRefGoogle Scholar