Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T12:06:54.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Buckling of a thin-layer Couette flow

Published online by Cambridge University Press:  24 November 2012

Anja C. Slim ,
Jeremy Teichman  and
L. Mahadevan
Anja C. Slim
Affiliation:
Department of Physics and School of Engineering and Applied Sciences, Harvard University, 29 Oxford Street, Cambridge, MA 02138, USA
Jeremy Teichman
Affiliation:
Institute for Defense Analyses, Virginia, USA
L. Mahadevan*
Affiliation:
Department of Physics and School of Engineering and Applied Sciences, Harvard University, 29 Oxford Street, Cambridge, MA 02138, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse the buckling stability of a thin, viscous sheet when subject to simple shear, providing conditions for the onset of the dominant out-of-plane modes using two models: (i) an asymptotic theory for the dynamics of a viscous plate, and (ii) the full Stokes equations. In either case, the plate is stabilized by a combination of viscous resistance, surface tension and buoyancy relative to an underlying denser fluid. In the limit of vanishing thickness, plates buckle at a shear rate 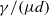independent of buoyancy, where 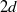is the plate thickness, 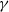is the average surface tension between the upper and lower surfaces, and 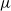is the fluid viscosity. For thicker plates stabilized by an equal surface tension at the upper and lower surfaces, at and above onset, the most unstable mode has moderate wavelength, is stationary in the frame of the centreline, spans the width of the plate with crests and troughs aligned at approximately 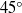to the walls, and closely resembles elastic shear modes. The thickest plates that can buckle have an aspect ratio (thickness/width) of approximately 0.6 and are stabilized only by internal viscous resistance. We show that the viscous plate model can only accurately describe the onset of buckling for vanishingly thin plates but provides an excellent description of the most unstable mode above onset. Finally, we show that, by modifying the plate model to incorporate advection and make the model material-frame-invariant, it is possible to extend its predictive power to describe relatively short, travelling waves.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Materials Processing Flows: Materials Processing Flows Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 694 , 10 March 2012 , pp. 5 - 28
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Balmforth, N. J., Craster, R. V. & Slim, A. C. 2008 On the buckling of elastic plates. Q. J. Mech. Appl. Maths 61 (2), 267–289.CrossRefGoogle Scholar
2. Benjamin, T. B. & Mullin, T. 1988 Buckling instabilities in layers of viscous liquid subjected to shearing. J. Fluid Mech. 195, 523–540.CrossRefGoogle Scholar
3. Biot, M. A. 1961 Theory of folding of stratified viscoelastic media and its implications in tectonics and orogenesis. Geol. Soc. Am. Bull. 72 (11), 1595–1620.CrossRefGoogle Scholar
4. Buckmaster, J. D., Nachman, A. & Ting, L. 1975 The buckling and stretching of a viscida. J. Fluid Mech. 69 (01), 1–20.CrossRefGoogle Scholar
5. Canuto, C., Hussaini, M. Y. & Quarteroni, A. 2007 Spectral Methods: Evolution to Complex Geometries and Applications to Fluid Dynamics. Springer.CrossRefGoogle Scholar
6. Chapple, W. M. 1968 A mathematical theory of finite-amplitude rock-folding. Geol. Soc. Am. Bull. 79, 47–68.CrossRefGoogle Scholar
7. Chiu-Webster, S. & Lister, J. R. 2006 The fall of a viscous thread onto a moving surface: a ‘fluid-mechanical sewing machine’. J. Fluid Mech. 569, 89–111.CrossRefGoogle Scholar
8. Friedrichs, K. O. & Dressler, R. F. 1961 A boundary-layer theory for elastic plates. Commun. Pure Appl. Maths 14 (1), 1–33.CrossRefGoogle Scholar
9. Gresho, P. M. 1991 Incompressible fluid dynamics: some fundamental formulation issues. Annu. Rev. Fluid Mech. 23 (1), 413–453.CrossRefGoogle Scholar
10. Howell, P. D. 1994 Extensional thin layer flows. PhD thesis, Oxford University.Google Scholar
11. Howell, P. D. 1996 Models for thin viscous sheets. Eur. J. Appl. Maths 7 (04), 321–343.CrossRefGoogle Scholar
12. Johnson, A. M. & Fletcher, R. C. 1994 Folding of Viscous Layers. Columbia University Press.Google Scholar
13. Mahadevan, L., Bendick, R. & Liang, H.-Y. 2010 Why subduction zones are curved. Tectonics 29, article TC6002.CrossRefGoogle Scholar
14. Mahadevan, L., Ryu, W. S. & Samuel, A. D. T. 1998 Fluid ‘rope trick’ investigated. Nature 392, 140, Addendum and correction, 2000, 403, 502.CrossRefGoogle Scholar
15. Ramberg, H. 1963 Fluid dynamics of viscous buckling applicable to folding of layered rocks. Bull. Am. Assoc. Petrol Geol. 47 (3), 484–505.Google Scholar
16. Rayleigh, J. W. S. 1945 Theory of Sound, vol. II, pp. 313–314. Dover.Google Scholar
17. Ribe, N. M. 2001 Bending and stretching of thin viscous sheets. J. Fluid Mech. 433, 135–160.CrossRefGoogle Scholar
18. Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
19. Silveira, R., Chaieb, S. & Mahadevan, L. 2000 Rippling instability of a collapsing bubble. Science 287, 1468–1471.CrossRefGoogle Scholar
20. Skorobogatiy, M. & Mahadevan, L. 2000 Folding of viscous sheets and filaments. Europhys. Lett. 52, 532.CrossRefGoogle Scholar
21. Slim, A. C., Balmforth, N. J., Craster, R. V. & Miller, J. C. 2009 Surface wrinkling of a channelized flow. Proc. R. Soc. Lond. A 465, 123–142.Google Scholar
22. Southwell, R. V. & Skan, S. W. 1924 On the stability under shearing forces of a flat elastic strip. Proc. R. Soc. Lond. A 105 (733), 582–607.Google Scholar
23. Suleiman, S. M. & Munson, B. R. 1981 Viscous buckling of thin fluid layers. Phys. Fluids 24, 1.CrossRefGoogle Scholar
24. Taylor, G. I. 1969 Instability of jets, threads, and sheets of viscous fluid. In Applied Mechanics: Proceedings of 12th International Congress, Stanford University (ed. Hétenyi, M. & Vincenti, W. G. ), pp. 321–330. Springer.Google Scholar
25. Teichman, J. A. 2002 Wrinkling and sagging of viscous sheets. PhD thesis, MIT.Google Scholar
26. Teichman, J. & Mahadevan, L. 2003 The viscous catenary. J. Fluid Mech. 478, 71–80.CrossRefGoogle Scholar
27. Timoshenko, S. P. & Woinowsky-Krieger, S. 1959 Theory of Plates and Shells. McGraw-Hill.Google Scholar
28. Trefethen, L. 2000 Spectral Methods in MATLAB. SIAM.CrossRefGoogle Scholar
29. Yarin, A. L. & Tchavdarov, B. M. 1996 Onset of folding in plane liquid films. J. Fluid Mech. 307, 85–99.CrossRefGoogle Scholar