1. Introduction
The Bretherton bubble, as the phenomenon is often referred, is the displacement of a viscous fluid by a long bubble of negligible viscosity through a regular tube. While this rather simple configuration was initially used to infer the flux of viscous fluid through a small capillary tube, it is the contribution by Bretherton (Reference Bretherton1961) to understanding the thickness of the film deposited during the transit of the bubble which has generated lasting and significant impact.
As the bubble is driven down the tube, some of the viscous fluid displaced is left on the walls due to the boundary condition at the solid–liquid interface. In being forced through the confines of the channel, the bubble is deformed from an otherwise static hemispherical shape into an elongated bubble separated from the solid by thin liquid films, and it is the surface tension acting on the liquid–air interface that resists this flow-driven deformation. Hence, it is the competition of viscous and capillary forces which ultimately sets the thickness of the deposited film (Aussillous & Quéré Reference Aussillous and Quéré2000).
Bretherton's approach to determining the film thickness, and hence the speed of the bubble, was twofold, hewing to what has become long tradition in the Journal of Fluid Mechanics. First, Bretherton formulated a mathematical model of the physical balance between surface tension and viscous forces to predict the profile of the thin film deposited, as characterised by the dimensionless ratio of viscous to capillary forces known as the capillary number,
written here in terms of the viscosity of the ambient fluid 
$\mu$, the measurable velocity of the bubble $U$ and the surface tension $\sigma$. The film thickness b was written in the form $b = rf(Ca)$, where $r$ is the tube radius. Second, having identified the key physical balance, Bretherton re-designed a new apparatus and performed additional experiments with a much higher level of detail and repeatability which helped confirm his theoretical insights for $Ca \ll 1$.
An elegant review of the scaling of this physical balance (Quéré Reference Quéré1999; Aussillous & Quéré Reference Aussillous and Quéré2000) matches the viscous stresses across the thin film, with gradients in the capillary pressure $\Delta p \sim \sigma /r$ on a length scale $l$ so that
The length scale over which the film deforms is found by matching the static and dynamic menisci,
and hence the film thickness is given by
with the constant $c$ determined by Bretherton's analysis (described below).
It is worth noting that the deposition of a thin film on a tube, and the interplay between viscous and capillary forces are reproduced (inside out) when a solid is withdrawn from a bath of fluid. In earlier comparable work, Landeau & Levich (Reference Landeau and Levich1942) and Derjaguin (Reference Derjaguin1943) considered the coating of film left on a plate as it is withdrawn from a bath of fluid and derived the now textbook result that the thickness of the coating on a withdrawn object $b \sim Ca^{2/3}$ (Quéré Reference Quéré1999).
2. A combination of approaches
A significant longstanding impact of Bretherton (Reference Bretherton1961) is the clarity of the asymptotic analysis used to model films surrounding the bubble. For sufficiently small $Ca \ll 1$, and where both gravity and inertia are negligible, the variations in the film surrounding the bubble occur on a length scale much larger than the film thickness ($b \ll l$ in the scaling argument above). Hence, a lubrication model can be posed balancing the viscous shear across the thin film with lateral gradients in the Laplace pressure, as described by the scaling in (1.2). Two limits are important in solving this model. At the centre of the bubble is the unknown, but nearly constant, minimum film thickness $b_0$ (region $C\to D$ in figure 1), which provides one model constraint. At the head of the bubble, where $b \gg b_0$, the curvature of the film, and hence the capillary pressure, assume a constant value (the film thickness is quadratic), providing the second model constraint. Note that by symmetry, the curvature of the bubble must be constant (though potentially different) at the front and the back. Finally, the origin is arbitrary ($x = 0$ in figure 1), providing the final model constraint. With these three constraints, imposed through an asymptotic analysis of the lubrication model, Bretherton (Reference Bretherton1961) found that the constant $c\simeq 0.643$ in (1.4), thus providing a quantitative prediction of the film thickness.
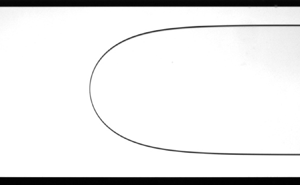
Figure 1. The original sketch of the Bretherton (Reference Bretherton1961) bubble, showing the quadratic nose in region $A\to B$, thin film in region $D\to C$ and trailing oscillatory film in region $E$.
Experimentally, it is a challenge to directly measure the thickness of the lubricating film on either side of the bubble. Rather than directly measure the film thickness, it is found that the speed of the bubble $U$ exceeds the speed of the fluid by an amount $UW$, where mass conservation requires and the result of the film model predicts that $W = 1.29 (3 Ca)^{2/3}$.
The fundamental observable is therefore the excess velocity of the bubble with respect to the fluid. Bretherton (Reference Bretherton1961) provided a new and extraordinarily careful set of experiments which clearly demonstrate a convincing agreement with the lubrication theory for $10^{-4} < Ca < 10^{-2}$. While this agreement is very encouraging, characteristically, it is the discussion of the discrepancies between theory and experiment for very small $Ca$ that is most informative. Here, Bretherton intuits many of the challenges and opportunities of the coming decades, describing for example the role of surface roughness (Chen Reference Chen1986), or of surface contaminants on the variability of the surface tension or indeed the action of the disjoining pressure for particularly thin films (de Gennes Reference de Gennes1985; Israelachvili Reference Israelachvili1985). Concurrent to Bretherton's theoretical and experimental work, Taylor (Reference Taylor1961) extended these experiments to much higher $Ca \sim 1$, a regime where inertia becomes important (Aussillous & Quéré Reference Aussillous and Quéré2000). Likewise, direct extensions of the original problem to understand the effect of the viscosity of the bubble have been investigated and found to modify only the numerical prefactor (Hodges, Jensen & Rallison Reference Hodges, Jensen and Rallison2004).
Finally, Bretherton (Reference Bretherton1961) extended both the theoretical analysis described above and the experimental investigation to study the rise of a bubble in a vertical tube. Here, the influence of gravity provides a balance between hydrostatic pressure and surface tension in the head and tail of the bubble where viscous forces are subdominant.
3. The long-lived impact of fundamental studies
The flow of the Bretherton bubble and the modelling approach so carefully described has played an important part in our understanding of flows at the smallest scales. The work has had a long lasting influence in designing and manipulating the flow of fluids at the smallest scales in microfluidic devices and it now includes, for example, the effects of surfactants, the flow of complex fluids and external drivers such as electrokinetics (Stone, Stroock & Ajdari Reference Stone, Stroock and Ajdari2004).
The flow of a deformable bubble in a capillary tube has also spurred a large volume of related work in biological fluid dynamics, often associated with the flow of deformable blood cells in the deformable capillaries (Lighthill Reference Lighthill1968; Secomb et al. Reference Secomb, Skalak, Ozkaya and Gross1986; Skalak, Ozkaya & Skalak Reference Skalak, Ozkaya and Skalak1989) or of airflow in and out of the lungs (Hazel & Heil Reference Hazel and Heil2003). Here again, the lubrication analysis described for a single bubble in a rigid capillary tube has been accommodated to incorporate the elastic pressure due to deformation of the elastic walls of the biological capillary, and the deformation of the blood cell as it transits the body.
The work of Bretherton also fits into a larger suite of fundamental problems in the flow of fluids in confined spaces. In an earlier classical work by Saffman & Taylor (Reference Saffman and Taylor1958), when a less viscous fluid is driven into a narrow gap (a Hele-Shaw cell) filled with a more viscous ambient, the interface is unstable to the formation of fingers. The process is an analogue for the instability of flows in porous media, with the resultant fingers sharing many hydrodynamic aspects with the single Bretherton bubble. Such studies have long formed the basis of modern work which seeks to understand the distribution of fluids in complex porous media (Zhao, MacMinn & Juanes Reference Zhao, MacMinn and Juanes2016). In Bretherton's introduction, it is also interesting to note the statement that motion of the bubble contacting the sidewalls, and therefore ‘filling the tube cross-section would involve infinite viscous stresses at the wall’. This statement alludes to the paradox of viscous stresses at a moving contact line so elegantly discussed by Huh & Scriven (Reference Huh and Scriven1971) and which has generated a significant literature of its own (de Gennes Reference de Gennes1985; Bonn et al. Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009).
Like a number of similar papers in early volumes of the Journal of Fluid Mechanics, the power and influence of Bretherton's work on the bubble in the tube is derived both from the simplicity and insight of the analysis and experimental observations. At a fundamental level, many subsequent works have extended the lubrication analysis in similar geometries, taking into account the variations in surface tension, the flexibility of the conduit walls or indeed by replacing the bubble with a deformable elastic capsule. Yet it is perhaps in the critical discussion of the results that Bretherton most clearly intuits major areas for fruitful fluid dynamical enquiry, many of which have subsequently filled the pages of this journal.
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0), which permits unrestricted re-use, distribution and reproduction, provided the original article is properly cited.
$A\to B$, thin film in region 
$D\to C$ and trailing oscillatory film in region 
$E$.
You have
Access
Open access
1. Introduction
The Bretherton bubble, as the phenomenon is often referred, is the displacement of a viscous fluid by a long bubble of negligible viscosity through a regular tube. While this rather simple configuration was initially used to infer the flux of viscous fluid through a small capillary tube, it is the contribution by Bretherton (Reference Bretherton1961) to understanding the thickness of the film deposited during the transit of the bubble which has generated lasting and significant impact.
As the bubble is driven down the tube, some of the viscous fluid displaced is left on the walls due to the boundary condition at the solid–liquid interface. In being forced through the confines of the channel, the bubble is deformed from an otherwise static hemispherical shape into an elongated bubble separated from the solid by thin liquid films, and it is the surface tension acting on the liquid–air interface that resists this flow-driven deformation. Hence, it is the competition of viscous and capillary forces which ultimately sets the thickness of the deposited film (Aussillous & Quéré Reference Aussillous and Quéré2000).
Bretherton's approach to determining the film thickness, and hence the speed of the bubble, was twofold, hewing to what has become long tradition in the Journal of Fluid Mechanics. First, Bretherton formulated a mathematical model of the physical balance between surface tension and viscous forces to predict the profile of the thin film deposited, as characterised by the dimensionless ratio of viscous to capillary forces known as the capillary number,
written here in terms of the viscosity of the ambient fluid
$\mu$, the measurable velocity of the bubble 
$U$ and the surface tension 
$\sigma$. The film thickness b was written in the form 
$b = rf(Ca)$, where 
$r$ is the tube radius. Second, having identified the key physical balance, Bretherton re-designed a new apparatus and performed additional experiments with a much higher level of detail and repeatability which helped confirm his theoretical insights for 
$Ca \ll 1$.
An elegant review of the scaling of this physical balance (Quéré Reference Quéré1999; Aussillous & Quéré Reference Aussillous and Quéré2000) matches the viscous stresses across the thin film, with gradients in the capillary pressure
$\Delta p \sim \sigma /r$ on a length scale 
$l$ so that
The length scale over which the film deforms is found by matching the static and dynamic menisci,
and hence the film thickness is given by
with the constant
$c$ determined by Bretherton's analysis (described below).
It is worth noting that the deposition of a thin film on a tube, and the interplay between viscous and capillary forces are reproduced (inside out) when a solid is withdrawn from a bath of fluid. In earlier comparable work, Landeau & Levich (Reference Landeau and Levich1942) and Derjaguin (Reference Derjaguin1943) considered the coating of film left on a plate as it is withdrawn from a bath of fluid and derived the now textbook result that the thickness of the coating on a withdrawn object
$b \sim Ca^{2/3}$ (Quéré Reference Quéré1999).
2. A combination of approaches
A significant longstanding impact of Bretherton (Reference Bretherton1961) is the clarity of the asymptotic analysis used to model films surrounding the bubble. For sufficiently small
$Ca \ll 1$, and where both gravity and inertia are negligible, the variations in the film surrounding the bubble occur on a length scale much larger than the film thickness (
$b \ll l$ in the scaling argument above). Hence, a lubrication model can be posed balancing the viscous shear across the thin film with lateral gradients in the Laplace pressure, as described by the scaling in (1.2). Two limits are important in solving this model. At the centre of the bubble is the unknown, but nearly constant, minimum film thickness 
$b_0$ (region 
$C\to D$ in figure 1), which provides one model constraint. At the head of the bubble, where 
$b \gg b_0$, the curvature of the film, and hence the capillary pressure, assume a constant value (the film thickness is quadratic), providing the second model constraint. Note that by symmetry, the curvature of the bubble must be constant (though potentially different) at the front and the back. Finally, the origin is arbitrary (
$x = 0$ in figure 1), providing the final model constraint. With these three constraints, imposed through an asymptotic analysis of the lubrication model, Bretherton (Reference Bretherton1961) found that the constant 
$c\simeq 0.643$ in (1.4), thus providing a quantitative prediction of the film thickness.
Figure 1. The original sketch of the Bretherton (Reference Bretherton1961) bubble, showing the quadratic nose in region
$A\to B$, thin film in region 
$D\to C$ and trailing oscillatory film in region 
$E$.
Experimentally, it is a challenge to directly measure the thickness of the lubricating film on either side of the bubble. Rather than directly measure the film thickness, it is found that the speed of the bubble
$U$ exceeds the speed of the fluid by an amount 
$UW$, where mass conservation requires and the result of the film model predicts that 
$W = 1.29 (3 Ca)^{2/3}$.
The fundamental observable is therefore the excess velocity of the bubble with respect to the fluid. Bretherton (Reference Bretherton1961) provided a new and extraordinarily careful set of experiments which clearly demonstrate a convincing agreement with the lubrication theory for
$10^{-4} < Ca < 10^{-2}$. While this agreement is very encouraging, characteristically, it is the discussion of the discrepancies between theory and experiment for very small 
$Ca$ that is most informative. Here, Bretherton intuits many of the challenges and opportunities of the coming decades, describing for example the role of surface roughness (Chen Reference Chen1986), or of surface contaminants on the variability of the surface tension or indeed the action of the disjoining pressure for particularly thin films (de Gennes Reference de Gennes1985; Israelachvili Reference Israelachvili1985). Concurrent to Bretherton's theoretical and experimental work, Taylor (Reference Taylor1961) extended these experiments to much higher 
$Ca \sim 1$, a regime where inertia becomes important (Aussillous & Quéré Reference Aussillous and Quéré2000). Likewise, direct extensions of the original problem to understand the effect of the viscosity of the bubble have been investigated and found to modify only the numerical prefactor (Hodges, Jensen & Rallison Reference Hodges, Jensen and Rallison2004).
Finally, Bretherton (Reference Bretherton1961) extended both the theoretical analysis described above and the experimental investigation to study the rise of a bubble in a vertical tube. Here, the influence of gravity provides a balance between hydrostatic pressure and surface tension in the head and tail of the bubble where viscous forces are subdominant.
3. The long-lived impact of fundamental studies
The flow of the Bretherton bubble and the modelling approach so carefully described has played an important part in our understanding of flows at the smallest scales. The work has had a long lasting influence in designing and manipulating the flow of fluids at the smallest scales in microfluidic devices and it now includes, for example, the effects of surfactants, the flow of complex fluids and external drivers such as electrokinetics (Stone, Stroock & Ajdari Reference Stone, Stroock and Ajdari2004).
The flow of a deformable bubble in a capillary tube has also spurred a large volume of related work in biological fluid dynamics, often associated with the flow of deformable blood cells in the deformable capillaries (Lighthill Reference Lighthill1968; Secomb et al. Reference Secomb, Skalak, Ozkaya and Gross1986; Skalak, Ozkaya & Skalak Reference Skalak, Ozkaya and Skalak1989) or of airflow in and out of the lungs (Hazel & Heil Reference Hazel and Heil2003). Here again, the lubrication analysis described for a single bubble in a rigid capillary tube has been accommodated to incorporate the elastic pressure due to deformation of the elastic walls of the biological capillary, and the deformation of the blood cell as it transits the body.
The work of Bretherton also fits into a larger suite of fundamental problems in the flow of fluids in confined spaces. In an earlier classical work by Saffman & Taylor (Reference Saffman and Taylor1958), when a less viscous fluid is driven into a narrow gap (a Hele-Shaw cell) filled with a more viscous ambient, the interface is unstable to the formation of fingers. The process is an analogue for the instability of flows in porous media, with the resultant fingers sharing many hydrodynamic aspects with the single Bretherton bubble. Such studies have long formed the basis of modern work which seeks to understand the distribution of fluids in complex porous media (Zhao, MacMinn & Juanes Reference Zhao, MacMinn and Juanes2016). In Bretherton's introduction, it is also interesting to note the statement that motion of the bubble contacting the sidewalls, and therefore ‘filling the tube cross-section would involve infinite viscous stresses at the wall’. This statement alludes to the paradox of viscous stresses at a moving contact line so elegantly discussed by Huh & Scriven (Reference Huh and Scriven1971) and which has generated a significant literature of its own (de Gennes Reference de Gennes1985; Bonn et al. Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009).
Like a number of similar papers in early volumes of the Journal of Fluid Mechanics, the power and influence of Bretherton's work on the bubble in the tube is derived both from the simplicity and insight of the analysis and experimental observations. At a fundamental level, many subsequent works have extended the lubrication analysis in similar geometries, taking into account the variations in surface tension, the flexibility of the conduit walls or indeed by replacing the bubble with a deformable elastic capsule. Yet it is perhaps in the critical discussion of the results that Bretherton most clearly intuits major areas for fruitful fluid dynamical enquiry, many of which have subsequently filled the pages of this journal.
Acknowledgements
The author thanks A. Juel and A. Hazel for insightful comments on the manuscript, and J. Lawless for the image used in the graphical abstract.
Declaration of interests
The author report no conflict of interest.