Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-27T01:12:08.922Z Has data issue: false hasContentIssue false
  • English
  • Français

Bubble coalescence in low-viscosity power-law fluids

Published online by Cambridge University Press:  04 September 2020

Pritish M. Kamat ,
Christopher R. Anthony  and
Osman A. Basaran Open the ORCID record for Osman A. Basaran [Opens in a new window]
Pritish M. Kamat
Affiliation:
Davidson School of Chemical Engineering, Purdue University, West Lafayette, IN47907, USA
Christopher R. Anthony
Affiliation:
Davidson School of Chemical Engineering, Purdue University, West Lafayette, IN47907, USA
Osman A. Basaran*
Affiliation:
Davidson School of Chemical Engineering, Purdue University, West Lafayette, IN47907, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

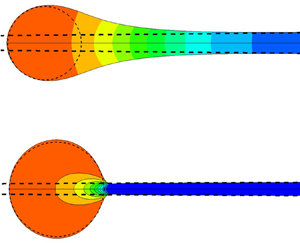
As two spherical gas bubbles of radii $\tilde {R}$ are brought together inside a liquid of density $\tilde {\rho }$, viscosity $\tilde {\mu }$ and surface tension $\tilde {\sigma }$, the liquid sheet separating them drains, thins and ultimately ruptures. The instant and location at which the bubbles make contact, and whereby a circular hole of vanishingly small radius is formed in the thin sheet, represent the occurrence of a finite-time singularity. The large curvature near the edge of the sheet where the hole has just formed, and where the two bubbles are now connected via a microscopic gas bridge, drives liquid to flow radially outward, causing the sheet to retract and the radius of the hole $\tilde {R}_{min}$ to increase with time. Recent work in this area has uncovered self-similarity and universal scaling regimes when two bubbles coalesce in a Newtonian fluid. Motivated by applications in which the exterior is a deformation-rate-thinning, power-law fluid, recent studies on bubble coalescence in Newtonian fluids are extended to coalescence in power-law fluids. In such fluids, viscosity decreases with deformation rate $\dot {\tilde {\gamma }}$ raised to the $n - 1$ power where $0 < n \le 1$ ($n = 1$ for a Newtonian fluid). Attention is focused here on power-law fluids that are slightly viscous at zero deformation rate, i.e. when the Ohnesorge number $Oh = \tilde {\mu }_{0}/(\tilde {\rho } \tilde {R} \tilde {\sigma })^{1/2}$ is small ($Oh \ll 1$) and where $\tilde {\mu }_0$ is the zero-deformation-rate viscosity. A combination of thin-film theory and three-dimensional, axisymmetric computations is used to probe the dynamics in the aftermath of the singularity. Heretofore unexplored regimes are uncovered, and criteria are developed for transitions between different regimes. The existence of a truly inviscid regime, predicted long ago by Keller (Phys. Fluids, vol. 26, 1983, pp. 3451–3453) and which comes into play as a purely geometrical limit of the free-surface shape, is also reported. New insights are presented on the much studied Newtonian limit beyond the initial regime reported by Munro et al. (J. Fluid Mech., vol. 773, 2015, R3). The paper concludes with a phase diagram in $(n, \tilde {R}_{min}/\tilde {R})$-space, where the index $n$ characterizes the fluid and $\tilde {R}_{min}/\tilde {R}$ the extent of coalescence, that highlights the various regimes and transitions between them.

JFM classification

Drops and Bubbles: Breakup/coalescence Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 902 , 10 November 2020 , A8
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Dow Inc., Lake Jackson, TX 77566, USA.

§

Present address: Convergent Science, Inc., Madison, WI 53719, USA.

References

REFERENCES

Anthony, C. R., Harris, M. T. & Basaran, O. A. 2020 Initial regime of drop coalescence. Phys. Rev. Fluids 5 (3), 033608.CrossRefGoogle Scholar
Anthony, C. R., Kamat, P. M., Thete, S. S., Munro, J. P., Lister, J. R., Harris, M. T. & Basaran, O. A. 2017 Scaling laws and dynamics of bubble coalescence. Phys. Rev. Fluids 2 (8), 083601.CrossRefGoogle Scholar
Ariffin, T. S. T., Yahya, E. & Husin, H. 2016 The rheology of light crude oil and water-in-oil-emulsion. Procedia Engng 148, 1149–1155.CrossRefGoogle Scholar
Aris, R. 1989 Vectors, Tensors and the Basic Equations of Fluid Mechanics. Dover.Google Scholar
Basaran, O. A., Gao, H. & Bhat, P. P. 2013 Nonstandard inkjets. Annu. Rev. Fluid Mech. 45 (1), 85–113.CrossRefGoogle Scholar
Bird, R. B., Armstrong, R. C. & Hassager, O. 1987 Dynamics of Polymeric Liquids. Vol. 1: Fluid Mechanics, 2nd edn. John Wiley and Sons.Google Scholar
Bird, R. B., Stewart, W. E. & Lightfoot, E. N. 1960 Transport Phenomena. John Wiley & Sons.Google Scholar
Boger, D. V. 2009 Rheology and the resource industries. Chem. Engng Sci. 64 (22), 4525–4536.CrossRefGoogle Scholar
Bolaños-Jiménez, R., Sevilla, A., Martínez-Bazán, C., van der Meer, D. & Gordillo, J. M. 2009 The effect of liquid viscosity on bubble pinch-off. Phys. Fluids 21 (7), 072103.CrossRefGoogle Scholar
Carrier, V. & Colin, A. 2003 Coalescence in draining foams. Langmuir 19 (11), 4535–4538.CrossRefGoogle Scholar
Christodoulou, K. N. & Scriven, L. E. 1992 Discretization of free surface flows and other moving boundary problems. J. Comput. Phys. 99 (1), 39–55.CrossRefGoogle Scholar
Culick, F. E. C. 1960 Comments on a ruptured soap film. J. Appl. Phys. 31 (6), 1128–1129.CrossRefGoogle Scholar
Debrégeas, G., de Gennes, G. P. & Brochard-Wyart, F. 1998 The life and death of viscous “bare” bubbles. Science 279 (5357), 1704–1701.Google Scholar
Deen, W. M. 2012 Analysis of Transport Phenomena, 2nd edn. Oxford University Press.Google Scholar
Denn, M. M. & Morris, J. F. 2014 Rheology of non-Brownian suspensions. Annu. Rev. Chem. Biomol. Engng 5, 203–228.CrossRefGoogle ScholarPubMed
Dickinson, E. & van Vliet, T. 2003 Food Colloids, Biopolymers and Materials. Royal Society of Chemistry.Google Scholar
Dinic, J., Jimenez, L. N. & Sharma, V. 2017 Pinch-off dynamics and dripping-onto-substrate (DoS) rheometry of complex fluids. Lab on a Chip 17 (3), 460–473.CrossRefGoogle ScholarPubMed
Doshi, P. & Basaran, O. A. 2004 Self-similar pinch-off of power law fluids. Phys. Fluids 16 (3), 585–593.CrossRefGoogle Scholar
Doshi, P., Suryo, R., Yildirim, O. E., McKinley, G. H. & Basaran, O. A. 2003 Scaling in pinch-off of generalized Newtonian fluids. J. Non-Newtonian Fluid Mech. 113 (1), 1–27.CrossRefGoogle Scholar
Dupré, M. A. 1867 Sixiè me memoire sur la theorie méchanique de la chaleur. Annales de chimie et de physique 4 (11), 194–220.Google Scholar
Eggers, J. 1993 Universal pinching of 3D axisymmetric free-surface flow. Phys. Rev. Lett. 71 (21), 3458–3460.CrossRefGoogle ScholarPubMed
Eggers, J. 2014 Post-breakup solutions of Navier–Stokes and Stokes threads. Phys. Fluids 26 (7), 072104.CrossRefGoogle Scholar
Fabiyi, M. & Larrea, A. 2013 Understanding the Alpha factor: studies of the rheological properties of sludge and their effect on oxygen transfer efficiencies from full scale systems. In Proceedings of the Water Environment Federation, pp. 305–314. Water Environment Federation.CrossRefGoogle Scholar
Feely, R., Sabine, C., Takahashi, T. & Wanninkhof, R. 2001 Uptake and storage of carbon dioxide in the ocean: the global CO2 survey. Oceanography 14 (4), 18–32.CrossRefGoogle Scholar
Ghannam, M. T., Hasan, S. W., Abu-Jdayil, B. & Esmail, N. 2012 Rheological properties of heavy & light crude oil mixtures for improving flowability. J. Petrol. Sci. Engng 81, 122–128.CrossRefGoogle Scholar
Gordillo, J. M. & Pérez-Saborid, M. 2006 Axisymmetric breakup of bubbles at high Reynolds numbers. J. Fluid Mech. 562, 303–312.CrossRefGoogle Scholar
Hilgenfeldt, S., Koehler, S. A. & Stone, H. A. 2001 Dynamics of coarsening foams: accelerated and self-limiting drainage. Phys. Rev. Lett. 86 (20), 4704–4707.CrossRefGoogle ScholarPubMed
Howell, P. D., Scheid, B. & Stone, H. A. 2010 Newtonian pizza: spinning a viscous sheet. J. Fluid Mech. 659, 1–23.CrossRefGoogle Scholar
Huisman, F. M., Friedman, S. R. & Taborek, P. 2012 Pinch-off dynamics in foams, emulsions and suspensions. Soft Matt. 8 (25), 6767–6774.CrossRefGoogle Scholar
Janhøj, T., Bom Frøst, M. & Ipsen, R. 2008 Sensory and rheological characterization of acidified milk drinks. Food Hydrocoll. 22 (5), 798–806.CrossRefGoogle Scholar
Jenkinson, I., Wyatt, T. & Malej, A. 1998 How visco-elastic properties of colloidal biopolymers modify rheological properties of seawater. In Progress and Trends in Rheology V (ed. Emri, I.), pp. 57–58. Steinkopff.CrossRefGoogle Scholar
Joshi, J. B. 2001 Computational flow modelling and design of bubble column reactors. Chem. Engng Sci. 56, 5893–5933.CrossRefGoogle Scholar
Keller, J. B. 1983 Breaking of liquid films and threads. Phys. Fluids 26 (12), 3451–3453.CrossRefGoogle Scholar
Keller, J. B. & Miksis, M. J. 1983 Surface tension driven flows. SIAM J. Appl. Maths 43 (2), 268–277.CrossRefGoogle Scholar
Larson, R. G. 2013 Constitutive Equations for Polymer Melts and Solutions: Butterworths Series in Chemical Engineering. Butterworth-Heinemann.Google Scholar
Lee, C. H., Moturi, V. & Lee, Y. 2009 Thixotropic property in pharmaceutical formulations. J. Control. Release 136 (2), 88–98.CrossRefGoogle ScholarPubMed
Lin, C.-C. & Segel, L. A. 1988 Mathematics Applied to Deterministic Problems in the Natural Sciences. Vol. 1. SIAM.CrossRefGoogle Scholar
Logan, J. D. 1987 Applied Mathematics, A Contemprary Approach, 2nd edn. John Wiley & Sons.Google Scholar
Mari, R., Seto, R., Morris, J. F. & Denn, M. M 2015 Discontinuous shear thickening in Brownian suspensions by dynamic simulation. Proc. Natl Acad. Sci. USA 112 (50), 15326–15330.CrossRefGoogle ScholarPubMed
Mougin, G. & Magnaudet, J. 2001 Path instability of a rising bubble. Phys. Rev. Lett. 88 (1), 014502.CrossRefGoogle ScholarPubMed
Munro, J. P., Anthony, C. R., Basaran, O. A. & Lister, J. R. 2015 Thin-sheet flow between coalescing bubbles. J. Fluid Mech. 773, R3.CrossRefGoogle Scholar
Munro, J. P. & Lister, J. R. 2018 Capillary retraction of the edge of a stretched viscous sheet. J. Fluid Mech. 844, R1.CrossRefGoogle Scholar
Notz, P. K. & Basaran, O. A. 2004 Dynamics and breakup of a contracting liquid filament. J. Fluid Mech. 512, 223–256.CrossRefGoogle Scholar
O'Horo, M. P. & Andrews, J. R. 1995 Initial stages of vapor-bubble nucleation in thermal ink-jet processes. In IS&T/SPIE's Symposium on Electronic Imaging: Science & Technology, pp. 182–188. International Society for Optics and Photonics.Google Scholar
Paulsen, J. D., Carmigniani, R., Kannan, A., Burton, J. C. & Nagel, S. R. 2014 Coalescence of bubbles and drops in an outer fluid. Nat. Commun. 5, 3182.CrossRefGoogle Scholar
Ranz, W. E. 1950 Some experiments on the dynamics of liquid films. J. Appl. Phys. 30, 1950–1955.CrossRefGoogle Scholar
Rayleigh, Lord 1891 Some applications of photography. Nature 44, 249–254.CrossRefGoogle Scholar
Renardy, M. 2002 Self-similar jet breakup for a generalized PTT model. J. Non-Newtonian Fluid. Mech. 103 (2000), 261–269.CrossRefGoogle Scholar
Ryder, J. F. & Yeomans, J. M. 2006 Shear thinning in dilute polymer solutions. J. Chem. Phys. 125 (19), 194906.CrossRefGoogle ScholarPubMed
Saulnier, F., Raphaël, E. & de Gennes, P.-G. 2002 Dewetting of thin-film polymers. Phys. Rev. E 66 (6), 061607.CrossRefGoogle ScholarPubMed
Savage, J. R., Caggioni, M., Spicer, P. T. & Cohen, I. 2010 Partial universality: pinch-off dynamics in fluids with smectic liquid crystalline order. Soft Matt. 6 (5), 892–895.CrossRefGoogle Scholar
Savva, N. & Bush, J. W. M. 2009 Viscous sheet retraction. J. Fluid Mech. 626, 211–240.CrossRefGoogle Scholar
Scriven, L. E. 1960 Dynamics of a fluid interface equation of motion for Newtonian surface fluids. Chem. Engng Sci. 12 (2), 98–108.CrossRefGoogle Scholar
Siegel, M. H., Merchuk, J. C. & Schugerl, K. 1986 Air-lift reactor analysis: interrelationships between riser, downcomer, and gas-liquid separator behavior, including gas recirculation effects. AIChE J. 32 (10), 1585–1596.CrossRefGoogle Scholar
Suri, S. & Banerjee, R. 2006 Biophysical evaluation of vitreous humor, its constituents and substitutes. Trends Biomater. Artif. Organs 20 (1), 72–77.Google Scholar
Suryo, R. & Basaran, O. A. 2006 Local dynamics during pinch-off of liquid threads of power law fluids: scaling analysis and self-similarity. J. Non-Newtonian Fluid Mech. 138 (2–3), 134–160.CrossRefGoogle Scholar
Taylor, G. I. 1959 The dynamics of thin theets of fluid. III. Disintegration of fluid sheets. Proc. R. Soc. Lond. A 253 (1274), 313–321.Google Scholar
Thete, S. S., Anthony, C. R., Basaran, O. A. & Doshi, P. 2015 Self-similar rupture of thin free films of power-law fluids. Phys. Rev. E 92 (2), 023014.CrossRefGoogle ScholarPubMed
Wilkes, E. D. & Basaran, O. A. 2001 Drop ejection from an oscillating rod. J. Colloid Interface Sci. 242 (1), 180–201.CrossRefGoogle Scholar
Wilkes, E. D., Phillips, S. D. & Basaran, O. A. 1999 Computational and experimental analysis of dynamics of drop formation. Phys. Fluids 11 (12), 3577–3598.CrossRefGoogle Scholar
Xu, X., Rice, S. A. & Dinner, A. R. 2013 Relation between ordering and shear thinning in colloidal suspensions. Proc. Natl Acad. Sci. USA 110 (10), 3771–3776.CrossRefGoogle ScholarPubMed