Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T18:08:13.516Z Has data issue: false hasContentIssue false
  • English
  • Français

Bubble and conical forms of vortex breakdown in swirling jets

Published online by Cambridge University Press:  24 June 2019

Pradeep Moise Open the ORCID record for Pradeep Moise [Opens in a new window]  and
Joseph Mathew
Pradeep Moise*
Affiliation:
Department of Aerospace Engineering, Indian Institute of Science, Bengaluru 560012, India
Joseph Mathew
Affiliation:
Department of Aerospace Engineering, Indian Institute of Science, Bengaluru 560012, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Experimental investigations of laminar swirling jets had revealed a new form of vortex breakdown, named conical vortex breakdown, in addition to the commonly observed bubble form. The present study explores these breakdown states that develop for the Maxworthy profile (a model of swirling jets) at inflow, from streamwise-invariant initial conditions, with direct numerical simulations. For a constant Reynolds number based on jet radius and a centreline velocity of 200, various flow states were observed as the inflow profile’s swirl parameter 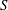$S$ (scaled centreline radial derivative of azimuthal velocity) was varied up to 2. At low swirl (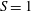$S=1$) a helical mode of azimuthal wavenumber 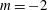$m=-2$ (co-winding, counter-rotating mode) was observed. A ‘swelling’ appeared at 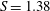$S=1.38$, and a steady bubble breakdown at 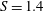$S=1.4$. On further increase to 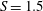$S=1.5$, a helical, self-excited global mode (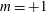$m=+1$, counter-winding and co-rotating) was observed, originating in the bubble’s wake but with little effect on the bubble itself – a bubble vortex breakdown with a spiral tail. Local and global stability analyses revealed this to arise from a linear instability mechanism, distinct from that for the spiral breakdown which has been studied using Grabowski profile (a model of wing-tip vortices). At still higher swirl (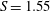$S=1.55$), a pulsating type of bubble breakdown occurred, followed by conical breakdown at 1.6. The latter consists of a large toroidal vortex confined by a radially expanding conical sheet, and a weaker vortex core downstream. For the highest swirls, the sheet was no longer conical, but curved away from the axis as a wide-open breakdown. The applicability of two classical inviscid theories for vortex breakdown – transition to a conjugate state, and the dominance of negative azimuthal vorticity – was assessed for the conical form. As required by the former, the flow transitioned from a supercritical to subcritical state in the vicinity of the stagnation point. The deviations from the predictions of the latter model were considerable.

JFM classification

Wakes/Jets: Jets Vortex Flows: Vortex breakdown
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 873 , 25 August 2019 , pp. 322 - 357
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Åkervik, E., Brandt, L., Henningson, D. S., Hœpffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18 (6), 068102.Google Scholar
Althaus, W., Brücker, C. & Weimer, M. 1995 Breakdown of slender vortices. In Fluid Vortices (ed. Green, S. I.), pp. 373–426. Springer Netherlands.Google Scholar
Althaus, W. & Weimer, M. 1998 Review of the Aachen work on vortex breakdown. In Proc., IUTAM Symposium on Dynamics of Slender Vortices (ed. Krause, E. & Gersten, K.), pp. 331–344. Kluwer Academic Publishers.Google Scholar
Balakrishna, N., Mathew, J. & Samanta, A.2019 BiGlobal stability of vortex ring. (under preparation).Google Scholar
Bayliss, A. & Turkel, E. 1992 Mappings and accuracy for Chebyshev pseudo-spectral approximations. J. Comput. Phys. 101 (2), 349–359.Google Scholar
Benjamin, T. B. 1962 Theory of the vortex breakdown phenomenon. J. Fluid Mech. 14 (4), 593–629.Google Scholar
Benjamin, T. B. 1967 Some developments in the theory of vortex breakdown. J. Fluid Mech. 28 (1), 65–84.Google Scholar
Billant, P., Chomaz, J.-M. & Huerre, P. 1998 Experimental study of vortex breakdown in swirling jets. J. Fluid Mech. 376, 183–219.Google Scholar
Blackburn, H. M. & Lopez, J. M. 2000 Symmetry breaking of the flow in a cylinder driven by a rotating end wall. Phys. Fluids 12 (11), 2698–2701.Google Scholar
Brown, G. L. & Lopez, J. M. 1990 Axisymmetric vortex breakdown. Part 2. Physical mechanisms. J. Fluid Mech. 221, 553–576.Google Scholar
Brücker, C. 1993 Study of vortex breakdown by particle tracking velocimetry (PTV). Part 2. Spiral-type vortex breakdown. Exp. Fluids 14 (1–2), 133–139.Google Scholar
Brücker, C. & Althaus, W. 1992 Study of vortex breakdown by particle tracking velocimetry (PTV). Exp. Fluids 13 (5), 339–349.Google Scholar
Chigier, N. A. & Chervinsky, A. 1967 Experimental investigation of swirling vortex motion in jets. Trans. ASME J. Appl. Mech. 34 (2), 443–451.Google Scholar
Chomaz, J.-M., Huerre, P. & Redekopp, L. G. 1991 A frequency selection criterion in spatially developing flows. Stud. Appl. Maths 84 (2), 119–144.Google Scholar
Escudier, M. 1984 Observations of the flow produced in a cylindrical container by a rotating endwall. Exp. Fluids 2 (4), 189–196.Google Scholar
Escudier, M. 1987 Confined vortices in flow machinery. Annu. Rev. Fluid Mech. 19, 27–52.Google Scholar
Escudier, M. 1988 Vortex breakdown: observations and explanations. Prog. Aerosp. Sci. 25 (2), 189–229.Google Scholar
Faler, J. H. & Leibovich, S. 1977 Disrupted states of vortex flow and vortex breakdown. Phys. Fluids 20 (9), 1385–1400.Google Scholar
Faler, J. H. & Leibovich, S. 1978 An experimental map of the internal structure of a vortex breakdown. J. Fluid Mech. 86, 313–335.Google Scholar
Fernández de la Mora, J. 2007 The fluid dynamics of Taylor cones. Annu. Rev. Fluid Mech. 39 (1), 217–243.Google Scholar
Fitzgerald, A. J., Hourigan, K. & Thompson, M. C. 2004 Towards a universal criterion for predicting vortex breakdown in swirling jets. In Proceedings of the Fifteenth Australasian Fluid Mechanics Conference (ed. Behnia, M., Lin, W. & McBain, G. D.). The University of Sydney.Google Scholar
Fraenkel, L. E. 1967 On Benjamin’s theory of conjugate vortex flows. J. Fluid Mech. 28 (1), 85–96.Google Scholar
Gallaire, F. & Chomaz, J.-M. 2003 Mode selection in swirling jet experiments: a linear stability analysis. J. Fluid Mech. 494, 223–253.Google Scholar
Gallaire, F., Rott, S. & Chomaz, J.-M. 2004 Experimental study of a free and forced swirling jet. Phys. Fluids 16 (8), 2907–2917.Google Scholar
Gallaire, F., Ruith, M., Meiburg, E., Chomaz, J.-M. & Huerre, P. 2006 Spiral vortex breakdown as a global mode. J. Fluid Mech. 549, 71–80.Google Scholar
Gore, R. W. & Ranz, W. E. 1964 Backflows in rotating fluids moving axially through expanding cross sections. AIChE J. 10 (1), 83–88.Google Scholar
Grabowski, W. J. & Berger, S. A. 1976 Solutions of the Navier–Stokes equations for vortex breakdown. J. Fluid Mech. 75 (3), 525–544.Google Scholar
Hall, M. G. 1972 Vortex breakdown. Annu. Rev. Fluid Mech. 4 (1), 195–218.Google Scholar
Healey, J. J. 2008 Inviscid axisymmetric absolute instability of swirling jets. J. Fluid Mech. 613, 1–33.Google Scholar
Heaton, C. J., Nichols, J. W. & Schmid, P. J. 2009 Global linear stability of the non-parallel Batchelor vortex. J. Fluid Mech. 629, 139–160.Google Scholar
Hernandez, V., Roman, J. E. & Vidal, V. 2005 SLEPc: a scalable and flexible toolkit for the solution of eigenvalue problems. ACM Trans. Math. Softw. 31 (3), 351–362.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22 (1), 473–537.Google Scholar
Kopecky, R. M. & Torrance, K. E. 1973 Initiation and structure of axisymmetric eddies in a rotating stream. Comput. Fluids 1 (3), 289–300.Google Scholar
Laizet, S. & Lamballais, E. 2009 High-order compact schemes for incompressible flows: a simple and efficient method with quasi-spectral accuracy. J. Comput. Phys. 228 (16), 5989–6015.Google Scholar
Laizet, S. & Li, N. 2011 Incompact3d, a powerful tool to tackle turbulence problems with up to O (105) computational cores. Intl J. Numer. Meth. Fluids 67, 1735–1757.Google Scholar
Lamballais, E., Fortuné, V. & Laizet, S. 2011 Straightforward high-order numerical dissipation via the viscous term for direct and large eddy simulation. J. Comput. Phys. 230 (9), 3270–3275.Google Scholar
Leibovich, S. 1978 The structure of vortex breakdown. Annu. Rev. Fluid Mech. 10, 221–246.Google Scholar
Leibovich, S. 1984 Vortex stability and breakdown – Survey and extension. AIAA J. 22 (9), 1192–1206.Google Scholar
Liang, H. & Maxworthy, T. 2005 An experimental investigation of swirling jets. J. Fluid Mech. 525, 115–159.Google Scholar
Lilley, D. G. 1977 Swirl flows in combustion: a review. AIAA J. 15 (8), 1063–1078.Google Scholar
Loiseleux, T. & Chomaz, J.-M. 2003 Breaking of rotational symmetry in a swirling jet experiment. Phys. Fluids 15 (2), 511–523.Google Scholar
Manoharan, K., Hansford, S., O’ Connor, J. & Hemchandra, S. 2015 Instability mechanism in a swirl flow combustor: precession of vortex core and influence of density gradient. In ASME. Turbo Expo: Power for Land, Sea, and Air, vol. 4A; paper number: GT2015-42985, p. V04AT04A073. ASME.Google Scholar
Meliga, P., Gallaire, F. & Chomaz, J.-M. 2012 A weakly nonlinear mechanism for mode selection in swirling jets. J. Fluid Mech. 699, 216–262.Google Scholar
Mitchell, A. M. & Delery, J. 2001 Research into vortex breakdown control. Prog. Aerosp. Sci. 37 (4), 385–418.Google Scholar
Mourtazin, D. & Cohen, J. 2007 The effect of buoyancy on vortex breakdown in a swirling jet. J. Fluid Mech. 571, 177–189.Google Scholar
Oberleithner, K., Paschereit, C. O., Seele, R. & Wygnanski, I. 2012 Formation of turbulent vortex breakdown: intermittency, criticality, and global instability. AIAA J. 50 (7), 1437–1452.Google Scholar
Oberleithner, K., Sieber, M., Nayeri, C. N., Paschereit, C. O., Petz, C., Hege, H. C., Noack, B. R. & Wygnanski, I. 2011 Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: stability analysis and empirical mode construction. J. Fluid Mech. 679, 383–414.Google Scholar
Ogus, G., Baelmans, M. & Vanierschot, M. 2016 On the flow structures and hysteresis of laminar swirling jets. Phys. Fluids 28 (12), 123604.Google Scholar
Pasche, S., Avellan, F. & Gallaire, F. 2018 Onset of chaos in helical vortex breakdown at low reynolds number. Phys. Rev. Fluids 3, 064701.Google Scholar
Pier, B. & Huerre, P. 2001 Nonlinear self-sustained structures and fronts in spatially developing wake flows. J. Fluid Mech. 435, 145–174.Google Scholar
Pradeep, M.2019 Bubble and conical forms of vortex breakdown in swirling jets. PhD thesis, Indian Institute of Science, unpublished.Google Scholar
Qadri, U., Mistry, D. & Juniper, M. 2013 Structural sensitivity of spiral vortex breakdown. J. Fluid Mech. 720, 558–581.Google Scholar
Rotunno, R. 2013 The fluid dynamics of tornadoes. Annu. Rev. Fluid Mech. 45 (1), 59–84.Google Scholar
Ruith, M. R., Chen, P. & Meiburg, E. 2004 Development of boundary conditions for direct numerical simulations of three-dimensional vortex breakdown phenomena in semi-infinite domains. Comput. Fluids 33 (9), 1225–1250.Google Scholar
Ruith, M. R., Chen, P., Meiburg, E. & Maxworthy, T. 2003 Three-dimensional vortex breakdown in swirling jets and wakes: direct numerical simulation. J. Fluid Mech. 486, 331–378.Google Scholar
Santhosh, R. & Basu, S. 2015 Acoustic response of vortex breakdown modes in a coaxial isothermal unconfined swirling jet. Phys. Fluids 27 (3), 043601.Google Scholar
Sarpkaya, T. 1971 On stationary and travelling vortex breakdowns. J. Fluid Mech. 45 (3), 545–559.Google Scholar
Snyder, D. O. & Spall, R. E. 2000 Numerical simulation of bubble-type vortex breakdown within a tube-and-vane apparatus. Phys. Fluids 12 (3), 603–608.Google Scholar
Squire, H. B.1960 Analysis of the ‘vortex breakdown’ phenomenon, Part 1. Tech. Rep. Imperial College of Science and Technology Aeronautics Department Report No. 102.Google Scholar
Stevens, J. L., Lopez, J. M. & Cantwell, B. J. 1999 Oscillatory flow states in an enclosed cylinder with a rotating endwall. J. Fluid Mech. 389, 101–118.Google Scholar
Syred, N. & Beer, J. M. 1974 Combustion in swirling flows: a review. Combust. Flame 23 (2), 143–201.Google Scholar
Wang, S. & Rusak, Z. 1997 The dynamics of a swirling flow in a pipe and transition to axisymmetric vortex breakdown. J. Fluid Mech. 340, 177–223.Google Scholar

Moise and Mathew supplementary movie 1

Axial velocity contours on z = 0 plane at different times for the pulsating BVB observed at S = 1.56. The low frequency modulations associated with the unsteady flow can be observed from the figure, which is a characteristic of the pulsating type of BVB.

Download Moise and Mathew supplementary movie 1(Video)
Video 4.1 MB

Moise and Mathew supplementary movie 2

Temporal evolution of three-dimensional streamlines based on instantaneous velocity fields is shown for pulsating BVB observed at S = 1.56. The intermittent formation of a closed set of streamlines that delineate a toroidal structure are correlated with the pulsating temporal behaviour characteristic of this flow. It is noted that the streamlines originate from equispaced points along the line segment y = -0.5 to 0.5 for x = 3.5 and z = 0. The toroidal structure observed is the intermittent ‘second cell’ while the other permanent toroidal structure associated with the bubble is not highlighted here for clarity, but can be seen in figure 8.

Download Moise and Mathew supplementary movie 2(Video)
Video 9.8 MB

Moise and Mathew supplementary movie 3

Temporal evolution for the case of S = 1.6 shown using axial velocity contours on z = 0 plane at different times. Past initial transients, a long-time state of CVB can be observed starting from approximately t = 3000. The dynamic features and slow temporal changes in the conical sheet’s structure can be observed.

Download Moise and Mathew supplementary movie 3(Video)
Video 9.4 MB

Moise and Mathew supplementary movie 4

Cross-sectional features of CVB at S = 1.6 are highlighted using axial velocity contours plane at different times. The flow remains axisymmetric in the upstream regions, but non-axisymmetric features can be observed downstream. The conical sheet is seen to slowly rotate with time.

Download Moise and Mathew supplementary movie 4(Video)
Video 1.4 MB