Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Karyappa, Rahul B.
Deshmukh, Shivraj. D.
and
Thaokar, Rochish. M.
2014.
Deformation of an elastic capsule in a uniform electric field.
Physics of Fluids,
Vol. 26,
Issue. 12,
Karyappa, Rahul B.
and
Thaokar, Rochish M.
2014.
Electric-Field-Assisted Formation of Nonspherical Microcapsules.
Langmuir,
Vol. 30,
Issue. 34,
p.
10270.
Mhatre, Sameer
Deshmukh, Shivraj
and
Thaokar, Rochish. M.
2015.
Electrocoalescence of a drop pair.
Physics of Fluids,
Vol. 27,
Issue. 9,
Yan, Haipeng
He, Limin
Luo, Xiaoming
Wang, Jing
Huang, Xin
Lü, Yuling
and
Yang, Donghai
2015.
Investigation on Transient Oscillation of Droplet Deformation before Conical Breakup under Alternating Current Electric Field.
Langmuir,
Vol. 31,
Issue. 30,
p.
8275.
Mhatre, S.
Vivacqua, V.
Ghadiri, M.
Abdullah, A.M.
Al-Marri, M.J.
Hassanpour, A.
Hewakandamby, B.
Azzopardi, B.
and
Kermani, B.
2015.
Electrostatic phase separation: A review.
Chemical Engineering Research and Design,
Vol. 96,
Issue. ,
p.
177.
Mohamed, A. Said
Lopez-Herrera, Jose M.
Herrada, Miguel A.
Modesto-Lopez, Luis B.
and
Gañán-Calvo, Alfonso M.
2016.
Effect of a Surrounding Liquid Environment on the Electrical Disruption of Pendant Droplets.
Langmuir,
Vol. 32,
Issue. 27,
p.
6815.
Karyappa, Rahul B.
Naik, Ankita V.
and
Thaokar, Rochish M.
2016.
Electroemulsification in a Uniform Electric Field.
Langmuir,
Vol. 32,
Issue. 1,
p.
46.
Tadavani, Somayeh Khajehpour
Munroe, James R.
and
Yethiraj, Anand
2016.
The effect of confinement on the electrohydrodynamic behavior of droplets in a microfluidic oil-in-oil emulsion.
Soft Matter,
Vol. 12,
Issue. 45,
p.
9246.
Nganguia, H.
Young, Y.-N.
Layton, A. T.
Lai, M.-C.
and
Hu, W.-F.
2016.
Electrohydrodynamics of a viscous drop with inertia.
Physical Review E,
Vol. 93,
Issue. 5,
Pillai, Rohit
Berry, Joseph D.
Harvie, Dalton J. E.
and
Davidson, Malcolm R.
2016.
Electrokinetics of isolated electrified drops.
Soft Matter,
Vol. 12,
Issue. 14,
p.
3310.
He, Limin
Yan, Haipeng
Luo, Xiaoming
Cao, Juhang
Wang, Jing
and
Yang, Donghai
2017.
Study on the transient response of water-in-oil droplet interface to electric field.
Chemical Engineering Research and Design,
Vol. 118,
Issue. ,
p.
71.
Huang, Xin
He, Limin
Luo, Xiaoming
Yang, Donghai
Shi, Kaiyue
and
Yan, Haipeng
2017.
Breakup mode transformation of leaky dielectric droplet under direct current electric field.
International Journal of Multiphase Flow,
Vol. 96,
Issue. ,
p.
123.
Mikkelsen, Alexander
Rozynek, Zbigniew
Khobaib, Khobaib
Dommersnes, Paul
and
Fossum, Jon Otto
2017.
Transient deformation dynamics of particle laden droplets in electric field.
Colloids and Surfaces A: Physicochemical and Engineering Aspects,
Vol. 532,
Issue. ,
p.
252.
Luo, Xiaoming
Yan, Haipeng
Huang, Xin
Yang, Donghai
Wang, Jing
and
He, Limin
2017.
Breakup characteristics of aqueous droplet with surfactant in oil under direct current electric field.
Journal of Colloid and Interface Science,
Vol. 505,
Issue. ,
p.
460.
Zhang, Xu-Dong
Sun, Yue
Chen, Sen
and
Liu, Jing
2018.
Unconventional hydrodynamics of hybrid fluid made of liquid metals and aqueous solution under applied fields.
Frontiers in Energy,
Vol. 12,
Issue. 2,
p.
276.
Mikkelsen, A.
Khobaib, K.
Eriksen, F. K.
Måløy, K. J.
and
Rozynek, Z.
2018.
Particle-covered drops in electric fields: drop deformation and surface particle organization.
Soft Matter,
Vol. 14,
Issue. 26,
p.
5442.
Luo, Xiaoming
Yin, Haoran
Yan, Haipeng
Huang, Xin
Yang, Donghai
and
He, Limin
2018.
The electrocoalescence behavior of surfactant-laden droplet pairs in oil under a DC electric field.
Chemical Engineering Science,
Vol. 191,
Issue. ,
p.
350.
Luo, Xiaoming
Huang, Xin
Yan, Haipeng
Yang, Donghai
Wang, Jing
and
He, Limin
2018.
Breakup modes and criterion of droplet with surfactant under direct current electric field.
Chemical Engineering Research and Design,
Vol. 132,
Issue. ,
p.
822.
Liu, Jing
and
Yi, Liting
2018.
Liquid Metal Biomaterials.
Vol. 10,
Issue. ,
p.
19.
Lanauze, Javier A.
Sengupta, Rajarshi
Bleier, Blake J.
Yezer, Benjamin A.
Khair, Aditya S.
and
Walker, Lynn M.
2018.
Colloidal stability dictates drop breakup under electric fields.
Soft Matter,
Vol. 14,
Issue. 46,
p.
9351.
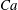 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Ca}$, which is the ratio of the electric to the capillary stress, a drop undergoes breakup. Although the steady-state deformation is independent of the viscosity ratio
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Ca}$, which is the ratio of the electric to the capillary stress, a drop undergoes breakup. Although the steady-state deformation is independent of the viscosity ratio 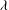 $\lambda $ of the drop and the medium phase, the breakup itself is dependent upon
$\lambda $ of the drop and the medium phase, the breakup itself is dependent upon 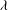 $\lambda $ and
$\lambda $ and 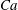 $\mathit{Ca}$. We perform a detailed experimental and numerical analysis of the axisymmetric shape prior to breakup (ASPB), which explains that there are three different kinds of ASPB modes: the formation of lobes, pointed ends and non-pointed ends. The axisymmetric shapes undergo transformation into the non-axisymmetric shape at breakup (NASB) before disintegrating. It is found that the lobes, pointed ends and non-pointed ends observed in ASPB give way to NASB modes of charged lobes disintegration, regular jets (which can undergo a whipping instability) and open jets, respectively. A detailed experimental and numerical analysis of the ASPB modes is conducted that explains the origin of the experimentally observed NASB modes. Several interesting features are reported for each of the three axisymmetric and non-axisymmetric modes when a drop undergoes breakup.
$\mathit{Ca}$. We perform a detailed experimental and numerical analysis of the axisymmetric shape prior to breakup (ASPB), which explains that there are three different kinds of ASPB modes: the formation of lobes, pointed ends and non-pointed ends. The axisymmetric shapes undergo transformation into the non-axisymmetric shape at breakup (NASB) before disintegrating. It is found that the lobes, pointed ends and non-pointed ends observed in ASPB give way to NASB modes of charged lobes disintegration, regular jets (which can undergo a whipping instability) and open jets, respectively. A detailed experimental and numerical analysis of the ASPB modes is conducted that explains the origin of the experimentally observed NASB modes. Several interesting features are reported for each of the three axisymmetric and non-axisymmetric modes when a drop undergoes breakup.

